胡思乱想(1) - The Mechanism of SVRG
The mechanism of SVRG
首先回顾一下,在strongly convex和\(L\)-smooth条件下,我们是可以去得到线性收敛的收敛速度,也就是\(\mathcal{O}(\log(\frac 1\epsilon))\)(这里省去了条件数\(\kappa\))。而在随机梯度下降的条件下,我们取得的收敛速度是次线性收敛速度,也就是\(\mathcal{O}(\frac 1 \epsilon)\)。
相比于确定性deterministic算法来说,随机性stochastic算法得到的梯度在期望上是一致的,但是样本选取的随机性为收敛的上界引入了方差(一般来说我们会假设这个方差上界是固定的)。为了解决引入的方差(固定值),我们通过让学习率/步长\(\eta=\mathcal{O}(1/t)\)以保证收敛。
SVRG的机制在于,在保证期望相同的同时,使得方差不再是一个固定的值,而是随着目标函数值的更新而逐渐下降的。具体而言
\(v_t\)是用来更新/搜索的方向,根据方差的公式\(\text{Var}(x) = \mathbb{E}[x^2] - \mathbb{E}[x]^2\),可以看到方差的第一项是跟损失函数\(P_{t-1}\)相关的,如果损失函数是下降的话,那么对应的方差也是下降的。

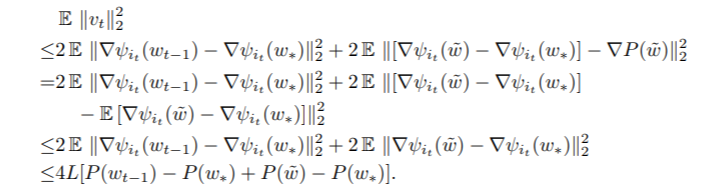

 浙公网安备 33010602011771号
浙公网安备 33010602011771号