Operator与优化

Relation

关系这个词跟映射有点相似，对于一个关系\(R\)，其是\((x, y)\)的一个集合集合。其中\(\text{dom }R=\{x|(x,y)\in R\}\)，\(R(x)=\{y\vert (x,y)\in R\}\)，其零集合是\(\{x| (x,y)\in R, y=0\}\)。

Operations on Relation

• inverse. \(R^{-1}=\{(y, x)\vert (x,y)\in R\}\)
• composition. \(RS=\{(x, y)\vert (x,z)\in R, (z,y)\in S\}\)
• scalar multiplication. \(\alpha R=\{(x, \alpha y)\vert (x,y)\in R\}\)
• addition. \(R+S=\{(x, y+z)\vert (x,y)\in R, (x,z)\in S\}\)
• resolvent operator. \(S=(I+\lambda R)^{-1}\)

通过以上的运算可以看出，relation有点类似于凸函数中epigraph的那种集合定义。

Monotone Operations

对于一个单调的relation \(F\)，其定义为

\[(u-v)^T(x-y)\geq 0 \]

对于任意的\((x, y), (u,v)\in R\). 一个最大单调\(F\)的定义为，没有其他单调relation包含\(F\)。

\(F\)是最大单调当且仅当\(F\)是一个连接的曲线，其斜率不存在负值。

Case: Subgradient \(F=\partial f(x)\)

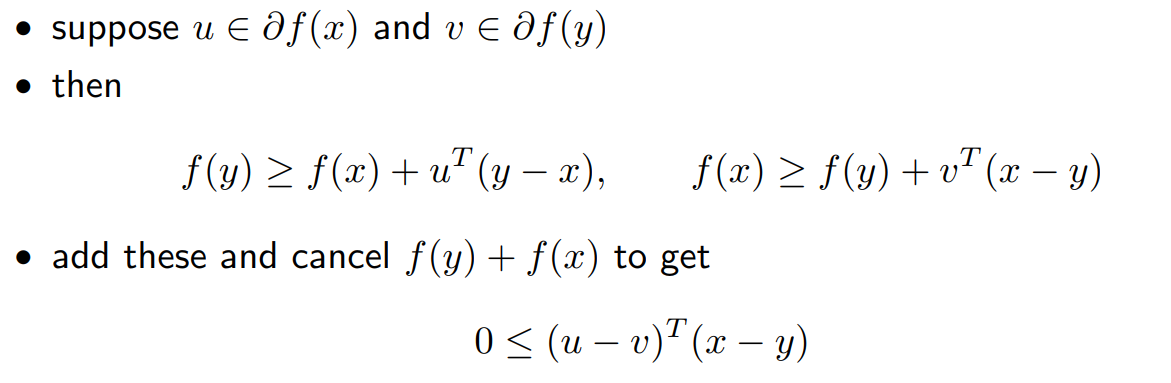
Nonexpansive and contractive operator

对于一个\(L-\)Lipschitz连续的operator \(F\)，其nonexpansive和contraction的定义分别为\(L=1\)和\(L<1\)。

Characters:

Resolvent operation and Cayley operator

对于一个relation \(F\)，当\(F\)是单调且nonexpansive时，\(R\) operator是contractive的。\(F\)的cayley operator定义为

\[C=2R-I=2(I+\lambda F)^{-1}-I \]

同样当F是单调的时候，其cayley operator \(C\)是nonexpansive。

Proof:

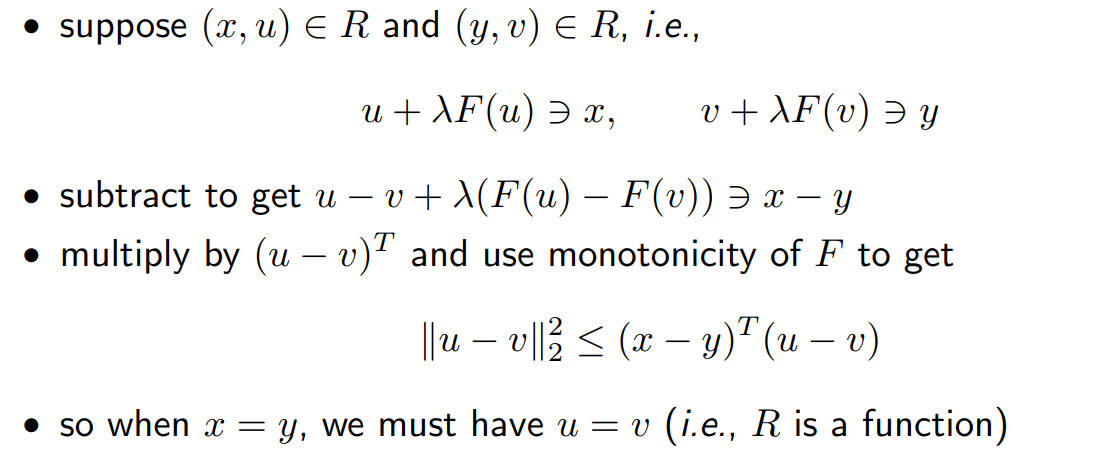
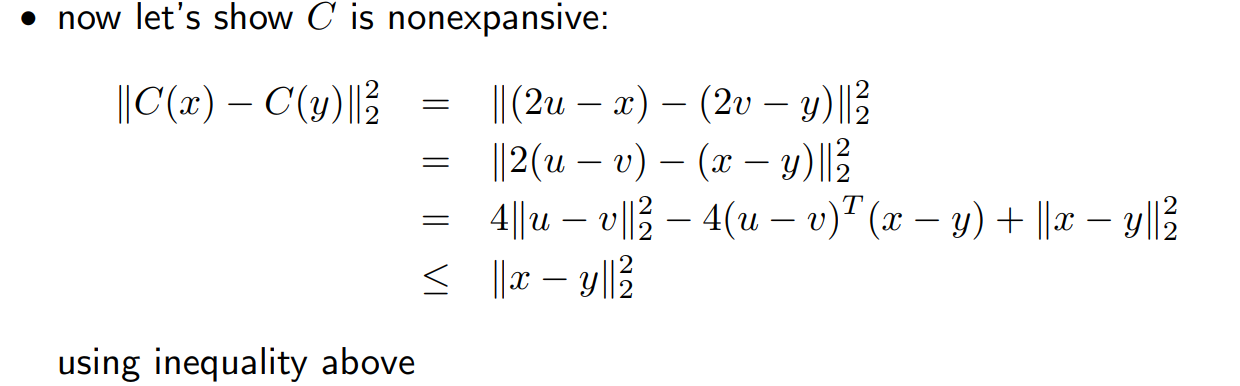
Case:

1. Proximal

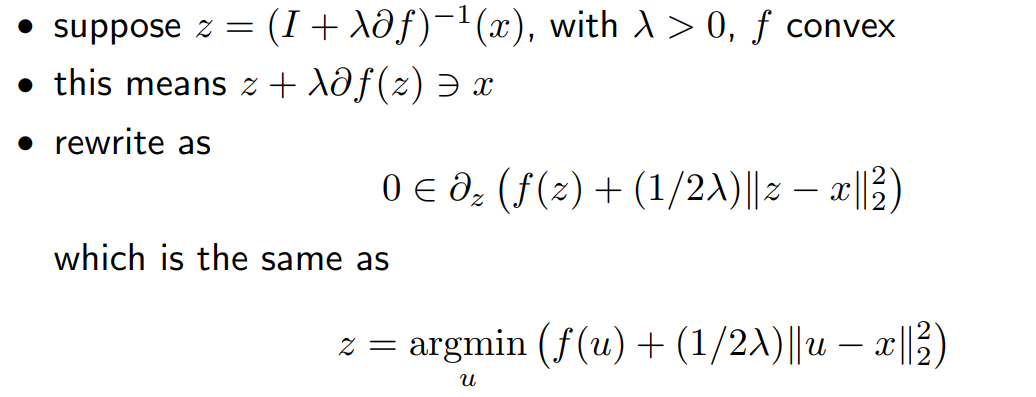
2. Indicator

Fixed point of operators & zero set of \(F\)

这里有个很重要的定理就是Cayley和resolvent的Fixed point等价于\(F\) relation的zero set。也就是

\[F(x)\in 0 \Leftrightarrow C(x)=x \Leftrightarrow R(x)=x \]

Theorem: Banach fixed point theorem

当\(F\)是contraction，dom \(F=R^n\)，那么\(F(x)\)会收敛到一个唯一的fixed point。

Damped iteration of a nonexpansive operator

相对于

\[x^{k+1}=F(x^k) \]

Damped iteration为一个\(x^k\)和\(F(x^k)\)的组合

\[x^{k+1} = \theta^k x^k+(1-\theta^k)F(x^k) \]

Proof:

Case:

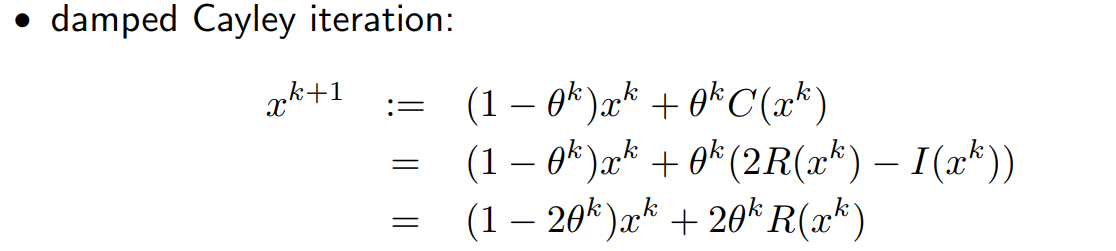
Operator Splitting

这里要解决的问题是一个relation \(F=A+B\)，单独队\(F\)进行求解可能比较麻烦而分开对\(A\)和\(B\)求解更简单。

Theorem: 如果A和B是maximal monotone，那么

\[0\in A(x)+B(x) \Leftrightarrow C_AC_B(z)=z \]

其中\(x=R_B(z)\)

Proof:

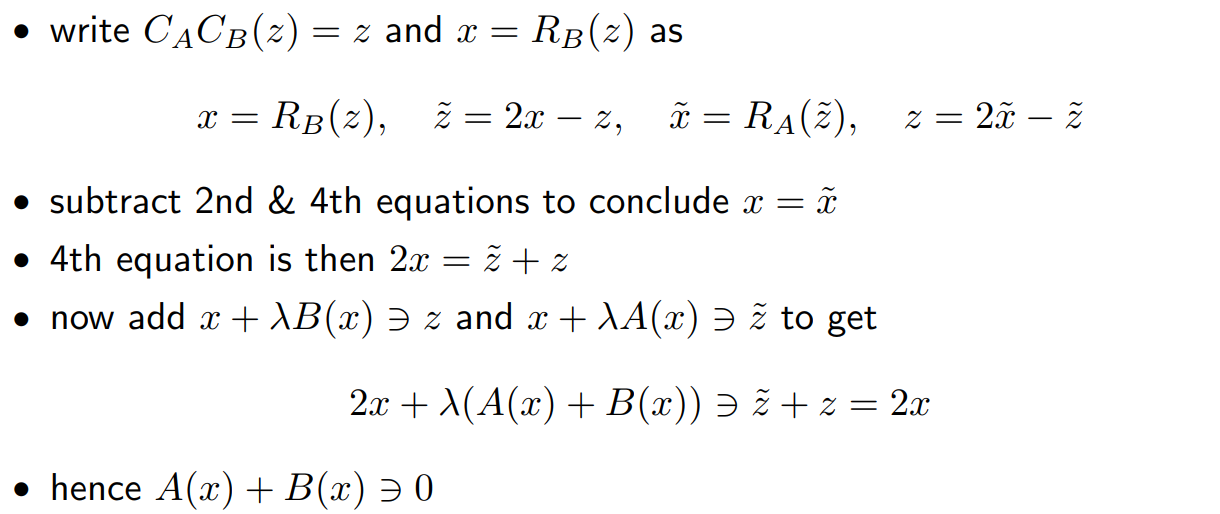
证明也是比较简单，使用定义就可以得到。

Peaceman-Rachford & Douglas-Rachfold Splitting

\[\begin{align} &\text{Peaceman-Rachford}:\qquad z^{k+1}=C_AC_B(z^k)\\ &\text{Douglas-Rachfold}:\qquad z^{k+1}=\frac 1 2(I+C_AC_B)(z^k)\\ \end{align} \]

1. Douglas-Rachfold updating

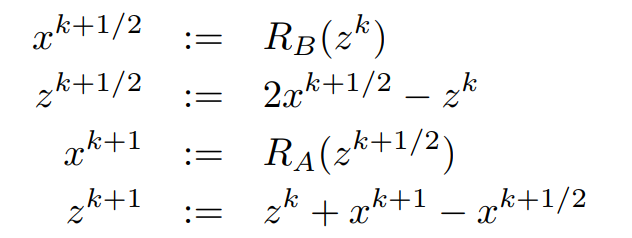
The last equation:

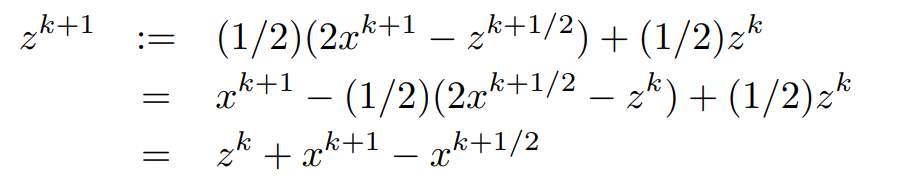
Case: Alternating direction method of multipliers

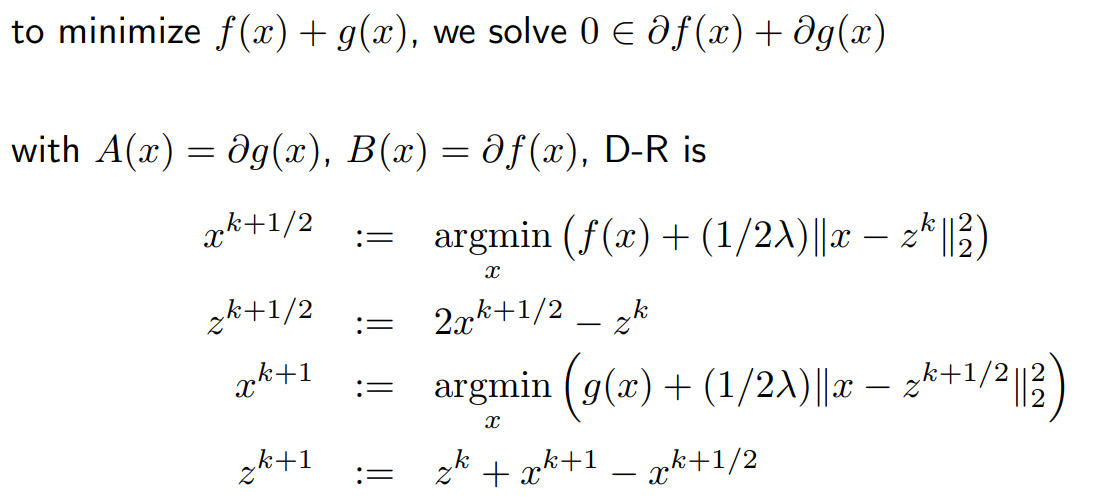
Case: Constrained optimization

2. Peaceman-Rachford updating

\[\begin{align}x^{k+\frac{1}{2}}&=\text{prox}_{\alpha f}(z^k)\\z^{k+\frac{1}{2}}&=2x^{k+\frac{1}{2}}-z^k\\x^{k+1}&=\text{prox}_{\alpha g}(z^{k+\frac{1}{2}})\\z^{k+1}&=2x^{k+1}-z^{k+\frac{1}{2}}\end{align} \]

Case: FedSplit, a consensus problem

对于loss函数\(F\)，以及consensus constrain，利用一阶方法求解最小值等价于

\[0\in \nabla F(x)+\mathcal{N}^{\bot} \]

其中\(\mathcal{N}^{\bot}\)为其consensus的normal corn。

上图为其论文中的算法流程，这里的\(A\) operator为\(\mathcal{N}^{\bot}\)，\(B\) operator为\(\nabla F\)而且由于\(x=\bar{z}\)在最后执行所以整个顺序都提前，并且算法中的第一步(a)直接整合了PR的中间两步。

Consensus Optimization

贴一下Boyd课程的代码吧（注释掉的是我修改的，更新就和公式一样了）

% Solves the QP
%       mininimze   (1/2)||Ax - b||_2^2
%       subject to  Fx <= g
% using D-R consensus. Note that the code has not been optimized for
% runtime and is only presened to give an idea of D-R consensu. For better
% performance, the inner loop should be run in parallel and should use a
% fast QP solver for small problems (e.g., CVXGEN).
%
% EE364b Convex Optimization II, S. Boyd
% Written by Eric Chu, 04/25/11
% 

close all; clear all
randn('state', 0); rand('state', 0);

%%% Generate problem instance
m = 1000;
n = 100;
k = 50;

xtrue = randn(n,1);
A = randn(m,n);
b = A*xtrue + randn(m,1);

F = randn(k,n);
g = F*xtrue;

%%% Use CVX to find solution
cvx_begin
    variable x(n)
    minimize ((1/2)*sum_square(A*x - b))
    subject to
        F*x <= g
cvx_end
xcvx = x;
fstar = cvx_optval; 
  
%%% Douglas-Rachford consensus splitting
N           = 10;      % number of subproblems
MAX_ITERS   = 50;
rho         = 200;

z           = zeros(n,N); 
xbar        = zeros(n,1);

for j = 1:MAX_ITERS,
    
    % x = prox_f(z), could be done in parallel
    for i = 1:N,
        Ai = A(m/N*(i-1) + 1:i*m/N,:);
        bi = b(m/N*(i-1) + 1:i*m/N);
        
        Fi = F(k/N*(i-1) + 1:i*k/N,:);
        gi = g(k/N*(i-1) + 1:i*k/N);
        
        % use CVX to solve prox operator
        zi = z(:,i);
        cvx_solver sdpt3
        cvx_begin quiet
            variable xi(n)
            minimize ( (1/2)*sum_square(Ai*xi - bi) + (rho/2)*sum_square(xi - zi) )
            subject to
                Fi*xi <= gi
        cvx_end
        x(:,i) = xi;
    end
    
    %% standard 
    %z_midterm = 2*x-z;
    %xbar_prev = xbar;
    %xbar = mean(z_midterm,2);
    
    %infeas(j) = sum(pos(F*xbar - g));
    %f(j) = (1/2)*sum_square(A*xbar - b);
    %z = z + (xbar*ones(1,N) - x);
    
    %% Boyd
    
    xbar_prev = xbar;
    xbar = mean(x,2);
    
    % record infeasibilities
    infeas(j) = sum(pos(F*xbar - g));
    
    % record objective value
    f(j) = (1/2)*sum_square(A*xbar - b);
    
    % update
    z = z + (xbar*ones(1,N) - x) + (xbar - xbar_prev)*ones(1,N);
end

%%% Make plots
subplot(2,1,1)
semilogy(1:MAX_ITERS, infeas);
ylabel('infeas'); set(gca, 'FontSize', 18); axis([1 MAX_ITERS 10^-2 10^2])
subplot(2,1,2)
plot(1:MAX_ITERS, f, [1 MAX_ITERS], [fstar fstar], 'k--');
xlabel('k'); ylabel('f'); axis([1 MAX_ITERS 300 2000]); set(gca, 'FontSize', 18);
print -depsc dr_consensus_qp.eps

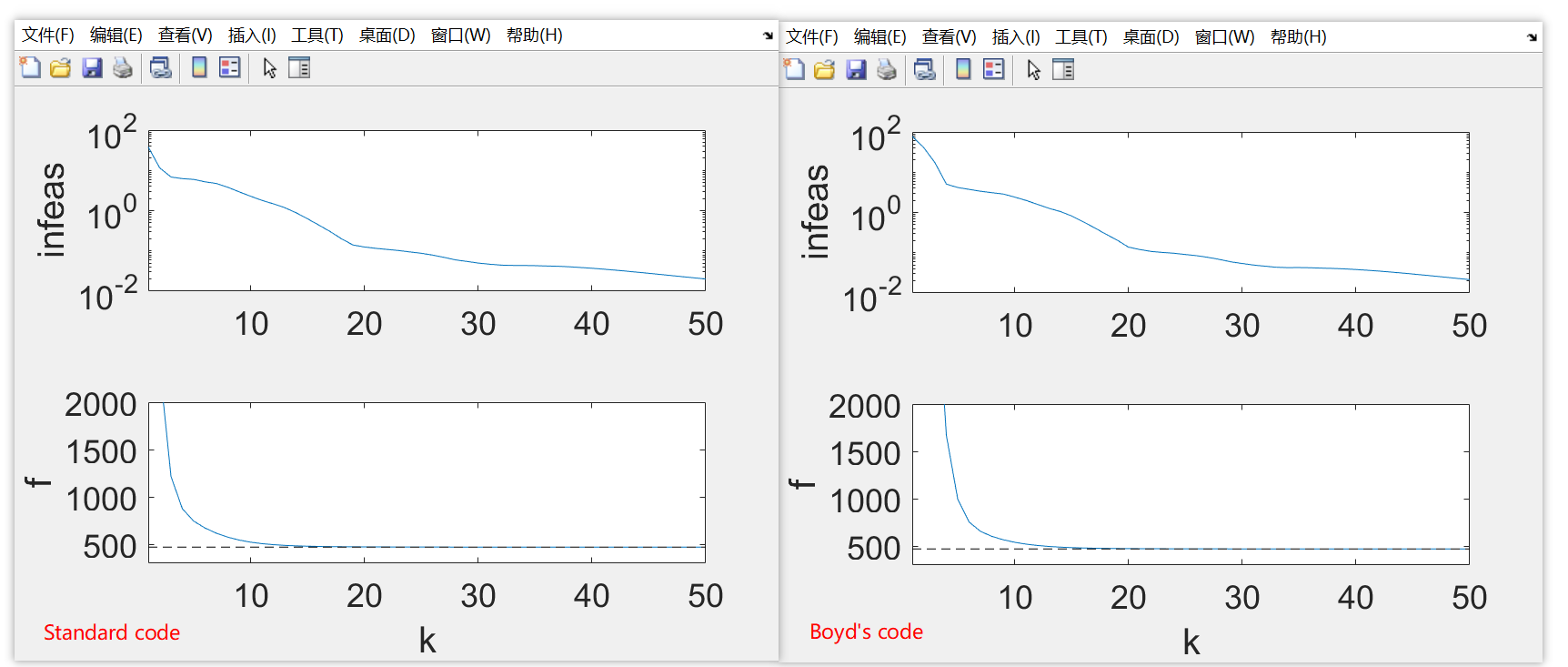
左边是我修改的，右边是Boyd的代码。看下来效果好像差不多，但是我还没搞懂他的代码为啥这样写。

参考资料

• Monotone Operators - Boyd
• Monotone Operator Splitting Methods - Boyd