论文笔记(4)—"Personalized Cross-Silo Federated Learning on Non-IID Data"
Methods
In their dissertation, in order to specialize clients' models, an intermediate result
Concretely, they solve the following problem:
where
Then,
The complete algorithm procedure is following
Note:
is the optimal solution of the above problem in k-th step. In my opinion, it's unlikely to find a closed solution and needs multi-local steps to find . Because authors didn't publish their code, I can't check the optimal condition of .
Convergence
For simplicity, there is only a convergence analysis in convex setting in this blog. Before elaborating the process, let take a look at their assumption:
As discussed in my previous bolg, we should prove
plugging in
we can have
we still should find the relationship between
Summary
- In their work, authors recognized that the similarity measure
- As above said, find
- The message passing mechanism is ambiguous for me

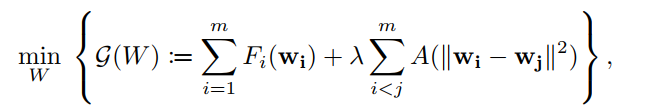
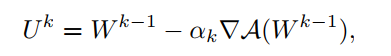
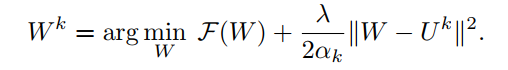

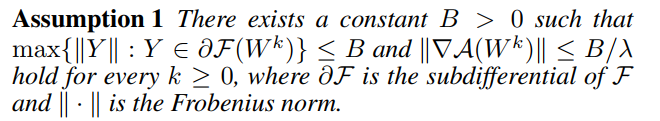
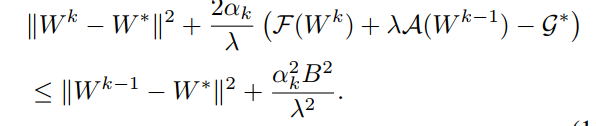


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· Manus的开源复刻OpenManus初探
· AI 智能体引爆开源社区「GitHub 热点速览」
· C#/.NET/.NET Core技术前沿周刊 | 第 29 期(2025年3.1-3.9)
· 从HTTP原因短语缺失研究HTTP/2和HTTP/3的设计差异