论文笔记(2)—"Adaptive Federated Optimization"
Intuition
Authors demonstrated that the gap between centralized and federated performance was caused by two reasons: 1)client drift, 2) a lack of adaptive.
Different from variance reduction methods, they extended federated learning with adaptive methods, like adam.
They rewrote the update rule of FedAvg
Let
The server learning rate
Convergence
Multi steps local update, concretely,
I'll only give my personal analysis of their proof of Theorem 1 and thoughts of Theorem 2 are similar.
Firstly, we should build relationships between
Furthermore, like in Adagrad, we will have
Now, we should bound these two terms
So far, there is no local training involving
To bound
As mentioned above,
Again, note that
In my opinion, how to bound
Honestly, local gradient
The second inequity is very rough and unclear. Known


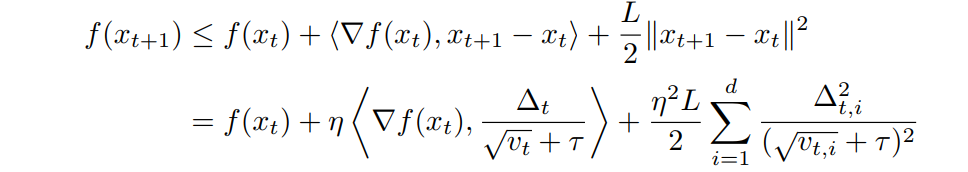
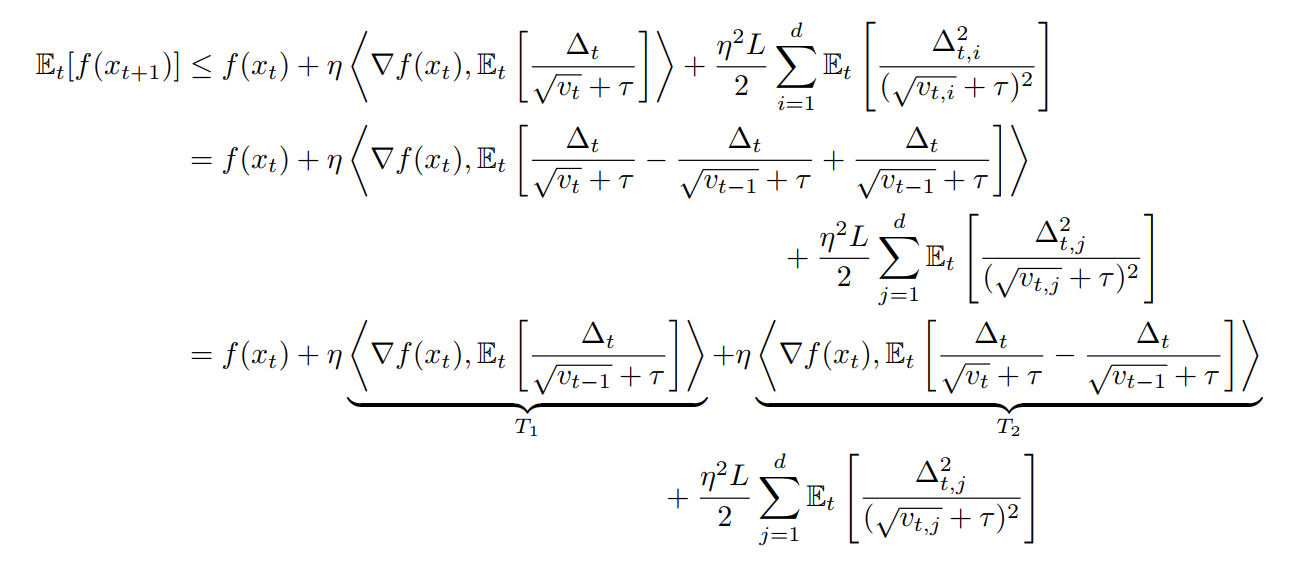
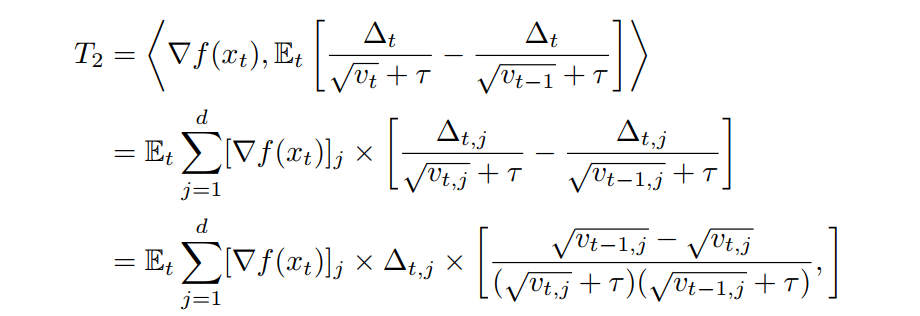
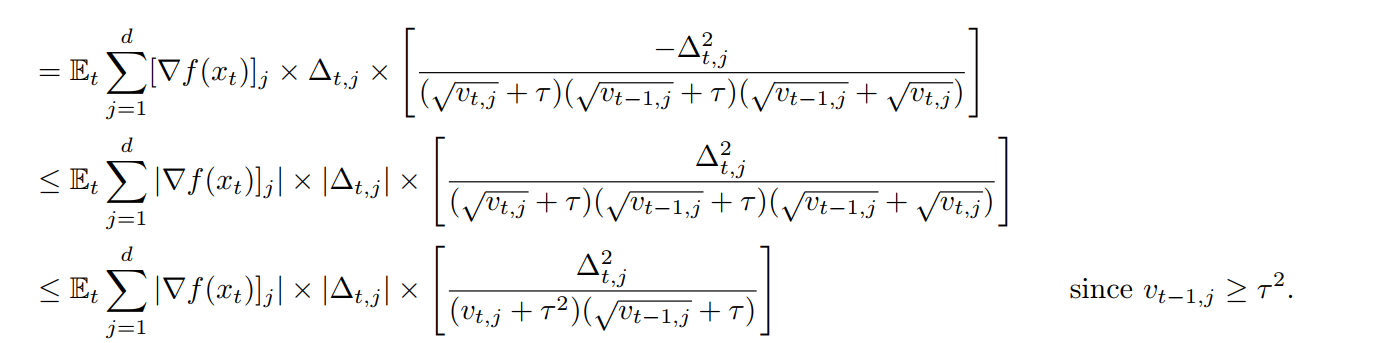
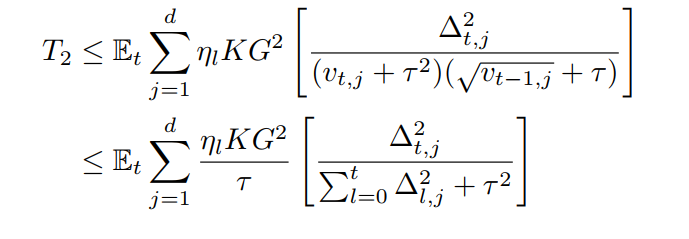
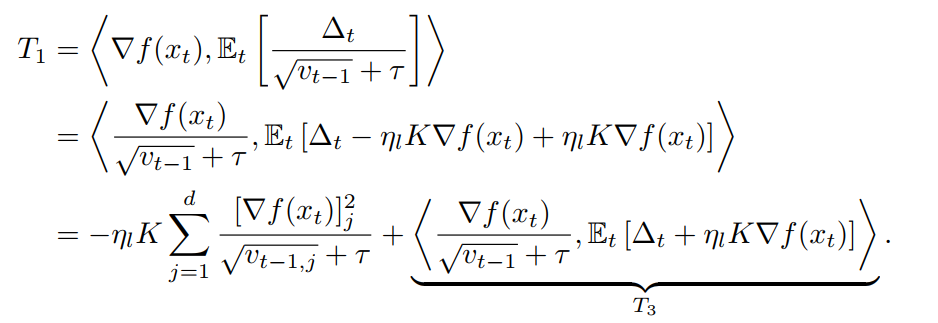
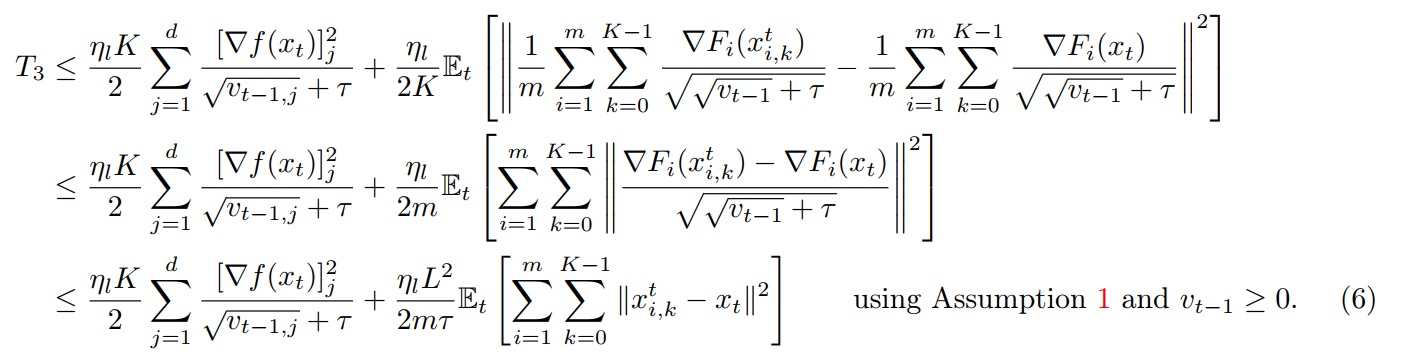
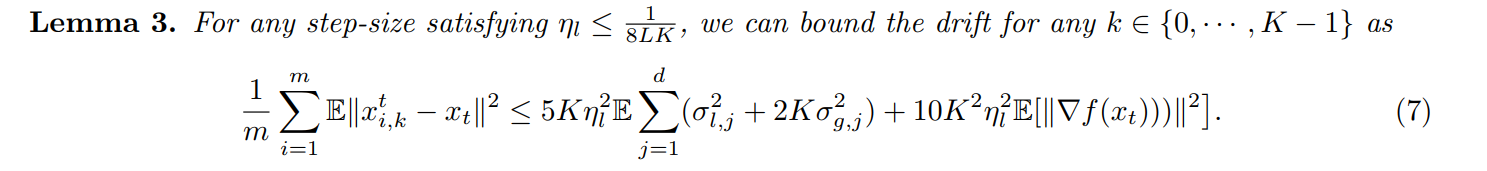
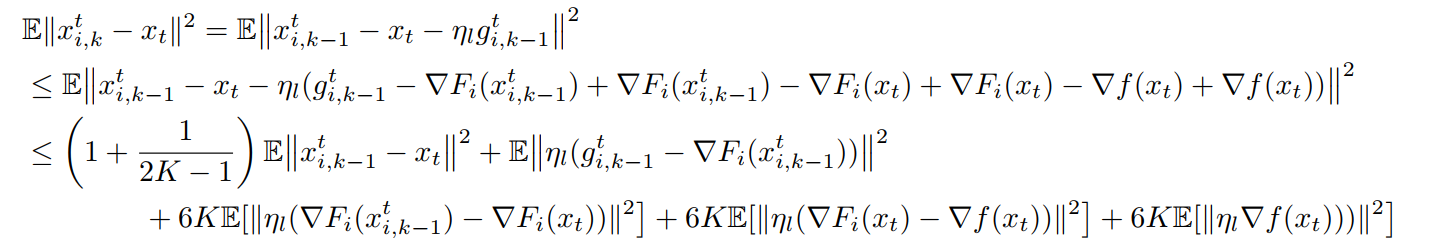


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· Manus的开源复刻OpenManus初探
· AI 智能体引爆开源社区「GitHub 热点速览」
· C#/.NET/.NET Core技术前沿周刊 | 第 29 期(2025年3.1-3.9)
· 从HTTP原因短语缺失研究HTTP/2和HTTP/3的设计差异