论文笔记(1)—"Clustered federated learning: Model-Agnostic distributed multi-Task optimization under privacy constraints"
Motivation
In this paper[1], authors presented a novel group based federated learning to solve incongruent data problem. In traditional FL methods, like FedAvg, assumes all clients' data coming from the same distribution. In fact, this assumption often fails.
Facing with incongruent data, clients won't get their optimal solutions though the system loss has been minimized. Autonomy is the most important characteristic of FL and it means clients will withdrawal from FL system if they haven't profit from it. The objective function seems not friendly for clients.
A simple way is to find solutions in each cluster. But, how segment the population? what is the segmentation criteria and where is the stopping point? Answers of above questions are presented in this paper [1]
Method
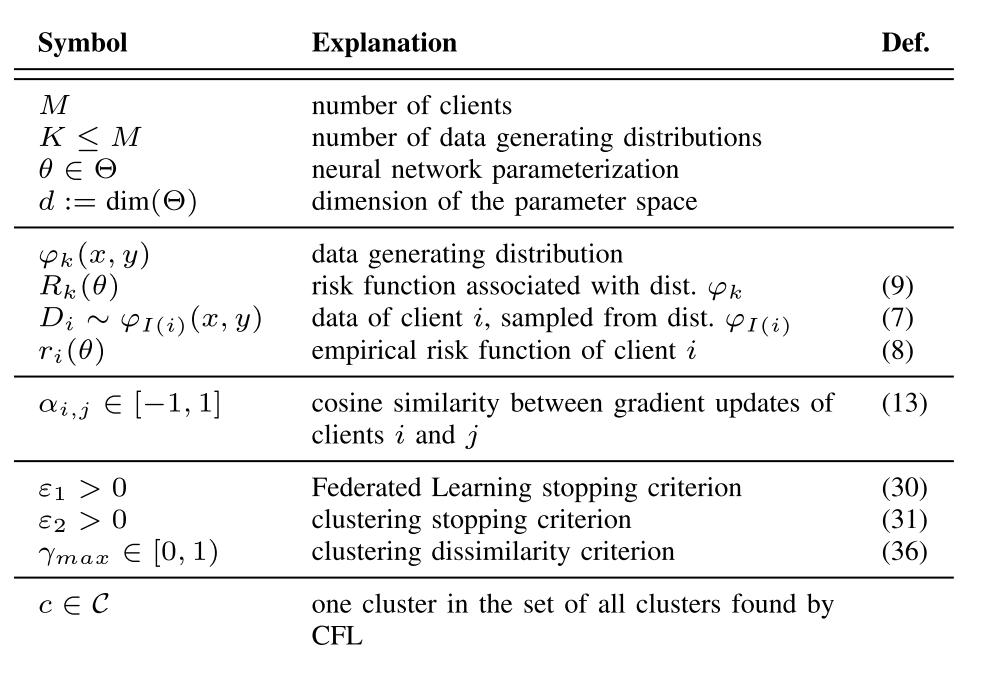
Notations
Key Ideas
similarity measurement
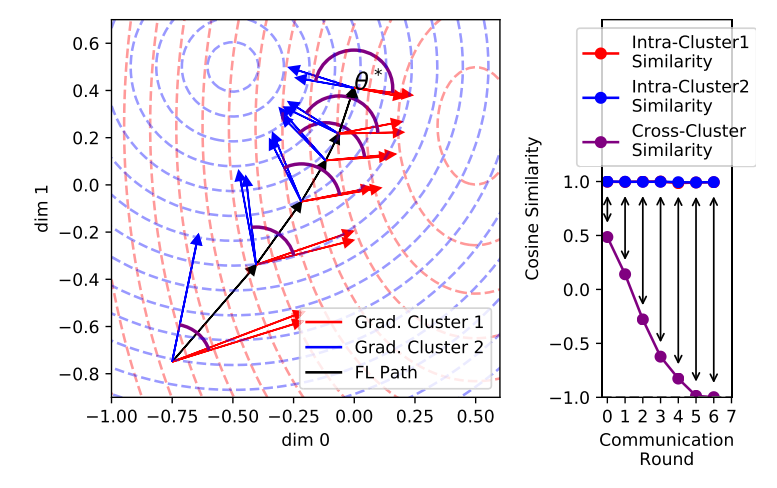
In this paper, authors used gradient consin similarity to segment population. Simply speaking, different clusters' gradient direction should have significant divergences and they used the consin similarity to segment.
Concretely, they used bipartitioning to divide whole clients set into two clusters. Detailed bipartitioning algorithm is following:
Personal Questions
My personal questions of their work are following:
- Despite of their intuition ideas, their basic assumption may fail in some scenarios. If all clusters' distribution have the same mean value and the shape of these distribution is like annulus, the gradient for binary classification problem is \(X^T(\hat{y}-y)\). Taking expectation on X, we have \(\mu(\hat{y}-y)\). If \(\mu\) is mildly lager than \(\hat y -y\), there will be little difference among all clusters. Worse more, if the data size of clients is small, \(\sigma(gradient)\) will be large and it definitely increase the error of segmentation.
- To compute the consin similarity, we should carefully choose which parts of network gradients can measure the similarity of clusters. For a complex network, concatenate all gradients in the network seems inappropriate, as they did in this work.
