Mirror Descent
文章整理了Mirror Descent相关的概念、基本定理,主要参考资料为[1]。
Mirror Descent
Mirror Descent可以看做Proximal的推广,其迭代流程如下
如果
式子中
- 拟合
- 在几何上与约束集合
- Bregman projection操作尽量简单
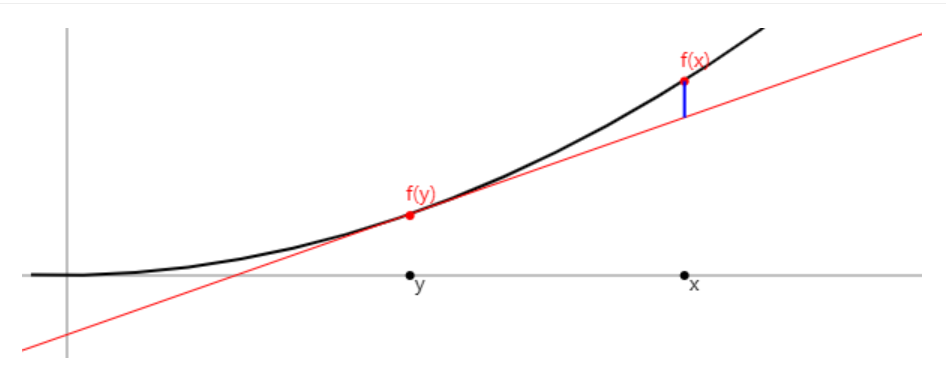
Bregman Divergence
要先说清楚Mirror Descent就先得说清楚bregman divergence,Bregman divergence是一种广义的距离度量,定义如下
对于一个在定义域
上强凸且可微的函数 ,定义Bregman divergence如下
Bregman divergence的详细含义和图示化的理解可以参看[2],简单来说,其表示的是
关于为什么说Bregman divergence是一种广义的度量以及详细的例子,可以参看[5]
Bregman divergence有如下几条简单的性质
- 如果
Three-point lemma
对于
,有下式成立
这个定理证明将Bregman Divergence展开就可以得到,详细过程[1]
Bregman Projection
Bregman Projection的定义如下
给定点
,其在约束集合 上的Bregman projection为
Generalized Pythagorean Theorem
令
,则
上面的定理说的就是在bregman divergence上定义的勾股定理,证明需要用到
再利用凸函数的性质,可以得到
再利用上面的Three-point lemma,即可得到上面的广义勾股定理,详细证明过程可以参看[1]。
Alternative form of Mirror Descent
回到最开始的mirror descent更新公式,
现在我们
因为这是我们没用在约束集
第一个式子可以通过,假设我们没有假设
上述方法求解原始问题的证明如下(
进一步的,如果
即
证明需要一些次梯度的理论,可以参看[3]的前几页内容。
详细证明过程推荐看原资料[1],
Convergence Analysis
凸且连续的问题
对于
如果
在上面的式子中,除去
本身的 和 以外,它的upper bound只跟如何选择 ,即度量 有关。在[1]中,也拿一个distribution的simplex例子对比了bregman divergence作为欧氏距离和KL divergence时收敛上届的差别。 在看收敛速度,虽然这里写的是
但是如果假定 是恒定恒定的话,结果应该是 的收敛速度
要证明上面的收敛性,需要先证明下面式子
现在只需要证明
现在我们有
除了上述的证明外,还可以参考一下[7],在阅读之前请先阅读Fenchel dual内容
这里,将
表示对偶空间的向量,那么
Gradient Descent & Fenchel dual
要讲清楚Gradient Descent和Mirror Descent区别到底在哪里,首先要讲一讲Fenchel dual。
首先
接下来我们讲一讲这个共轭函数的性质
- 当
我们可以看到,


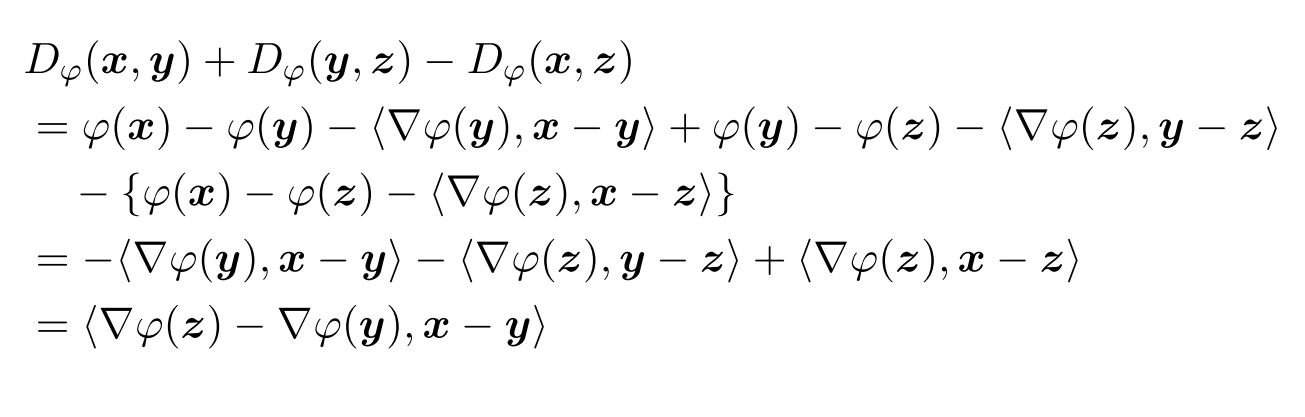



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· Manus的开源复刻OpenManus初探
· AI 智能体引爆开源社区「GitHub 热点速览」
· C#/.NET/.NET Core技术前沿周刊 | 第 29 期(2025年3.1-3.9)
· 从HTTP原因短语缺失研究HTTP/2和HTTP/3的设计差异