对拜占庭攻击鲁棒的异分布数据分布学习的梯度更新方法RSA

主体内容

这篇文章主要是在说，当在distributed leanring存在Byzantine attack，即可以向中央服务器发送任何内容导致最终结果出现bias，以及各个client之间不满足同分布的假设下该如何进行学习。

文章的formula如下：

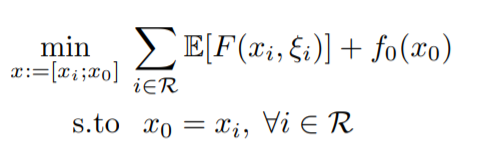
作者把中央服务器的参数和每个客户的参数分隔开，最后通过\(x_0=x_i\)的约束来同一两者。但是上面这个式子是无法优化的，作者近似出下面的式子，

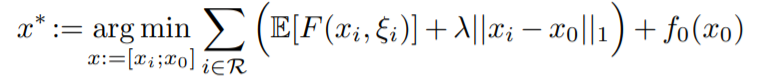
作者证明了当\(\lambda\)足够大的时候，上面两个式子的最优解是一样的。在优化的时候，对\(x_i\)和\(x_0\)分别进行优化，它们各自的更新公式如下：

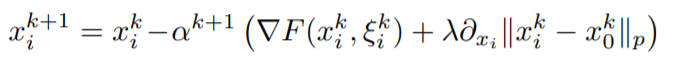
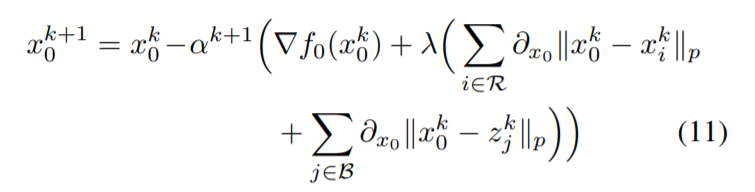
作者这样设计的算法有下面这样的优势：

同样面对Byzantine attack，相比于计算geometric mean之类的aggregation method这样的更新方式更为简便
算法设计时考虑了异分布的情况，更贴合实际
client和server的参数不一定相同，client可以保留personal的参数

定理证明

Proposition 1

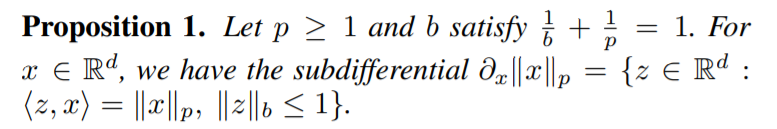
这个命题是在说，一个p-norm的subgradient集合等于另一个集合。

集合相等的证明需要证明两个集合中的元素都相同，或者证明两个集合相互包含。

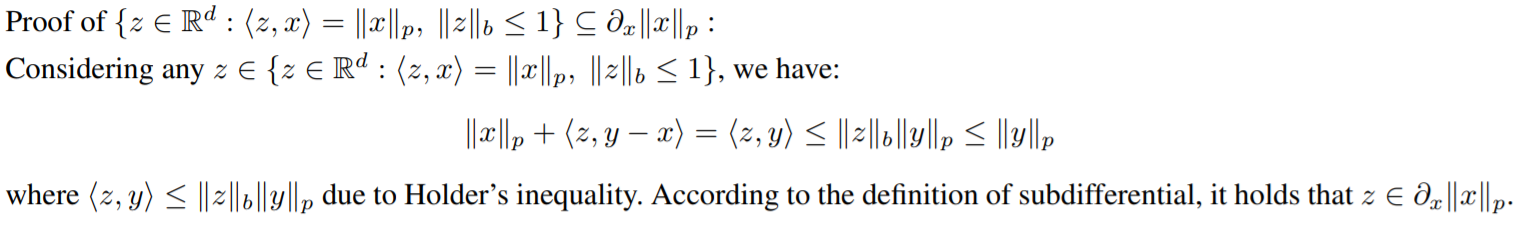
作者首先根据subgradient的定义证明了凡是属于\(\{z\in R^d:<z,x>=\Vert x\Vert_p, \Vert z\Vert_b\leq 1\}\)的元素都属于\(\partial_x\Vert x\Vert_p\)集合。

在证明\(\partial_x\Vert x\Vert_p\)的元素都属于\(\{z\in R^d:<z,x>=\Vert x\Vert_p, \Vert z\Vert_b\leq 1\}\)上，作者首先找到一个特殊的\(y=\Vert x\Vert_p x_z\)来得到\(\Vert x\Vert_p\Vert z\Vert_b=<z,x>\)。再通过对\(y\)进行特殊的赋值来得到\(\Vert z\Vert_b=1\)。需要注意的是p-norm在\(0\)处需要分开讨论。

Theroem 1

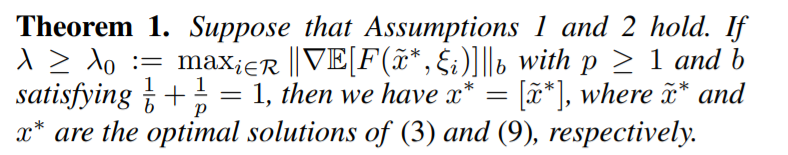
定理一是在说，当\(\lambda\)足够大的时候，两个formula得到的结果是一样的。

自己的想法：客户的目标函数都是convex的，加总得到的中央服务器的目标函数也是convex的，那么一定存在使得中央服务器最优的参数\(w^*\)，然后中央服务器\(w^*\)广播出去，每个client得到\(w^*\)。在我之前的理解下，如果client的数据是异分布的，那么他们有不同的行为习惯，那么应该得到不同的最后参数\(w^*_k\)。例如，一个客户喜欢自行车上班，另一个客户喜欢公交车上班，那么在给两人推荐的路线就应该是不同的。但是按照上面的分析，每个client得到的最终参数是相同的。我在想异分布和个性化到底存在什么联系？

这个证明特别有意思，

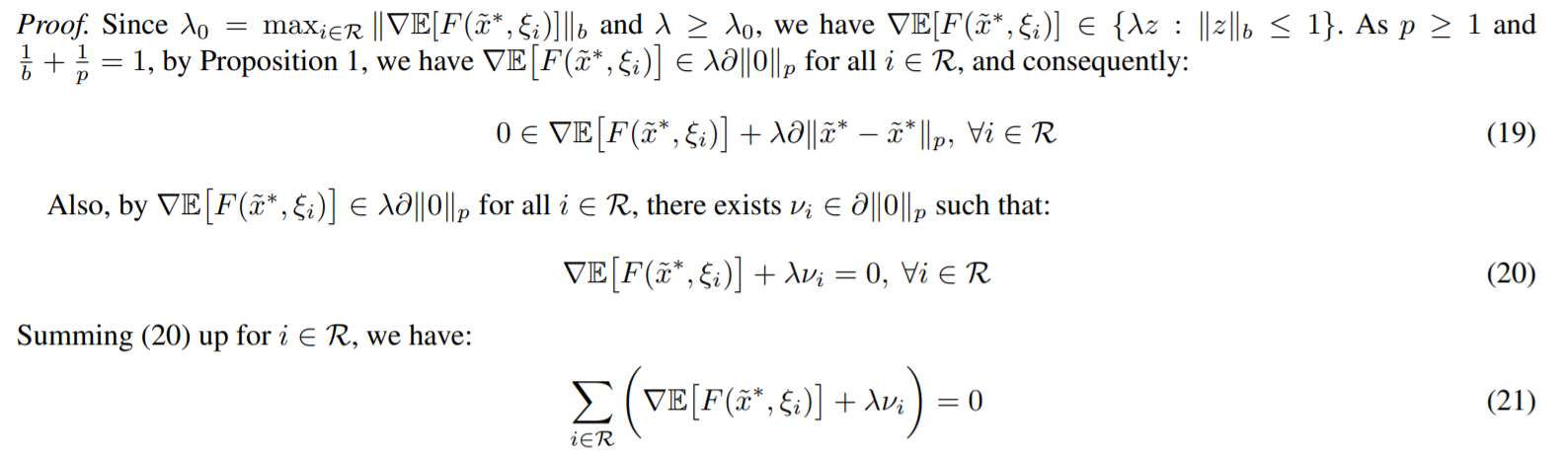
首先作者证明了\(\nabla E\Vert F(\tilde{x}^*, \xi_i) \Vert\in \lambda \Vert 0\Vert_p\)，然后因为\(\lambda \Vert 0\Vert_p\)这个集合是对称的，就得到了(20)，将所有的\(i\)汇总得到(21)。这个(21)的式子会利用第一个formula中的式子进行代换，

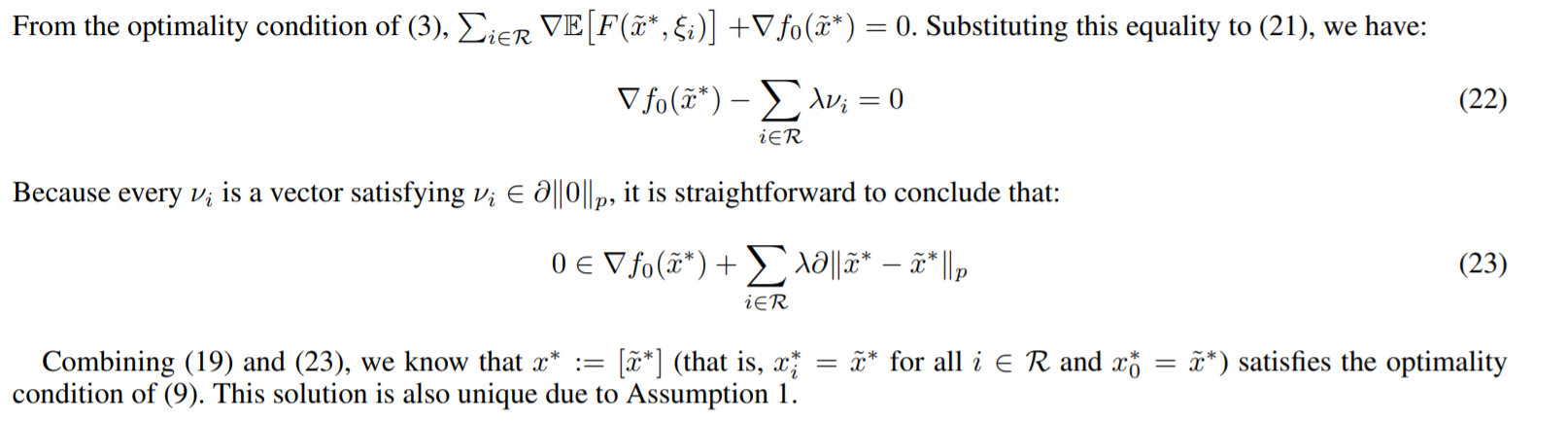
然后就得到了\(0\in \nabla f_0(\tilde{x}^*)+\sum\limits_{i\in\mathcal{R}} \lambda\partial \Vert \tilde{x}^*- \tilde{x}^*\Vert\)集合，那就证明\([\tilde{x}^*]\)是第二个formula的解。

其实这个定理不很直接易得的，第二个formula是第一个formula的slack版本，那么第一个都得到了那么第二个也是最优的。

Theorem 2

定理二涉及的就是最终收敛性的证明。终于到达最后的收敛性证明了，其实收敛性证明也是有规范可循的。

因为作者这里的\(x=[x_i; x_0]\)，所以client和server都需要证明一下啊但是基本上大同小异。

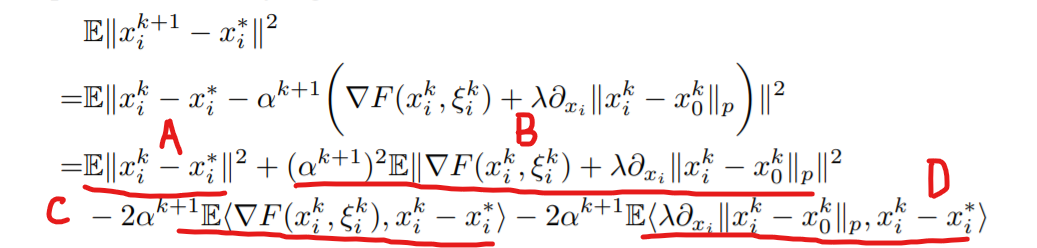
先来看regular work的update rule，其中\(A\)项是我们想要保留的，剩下的\(B\)、\(C\)和\(D\)都要进行放缩，要用到假设的convex，strongly-convex，bounded variance of gradient等假设来进行。

首先来看\(B\)项，因为涉及了\(E\Vert \nabla F(x_i^k, \xi_i^k)\Vert^2\)，首先不希望其中跟样本有关系然后我们假设的Bounded variance可以用到，

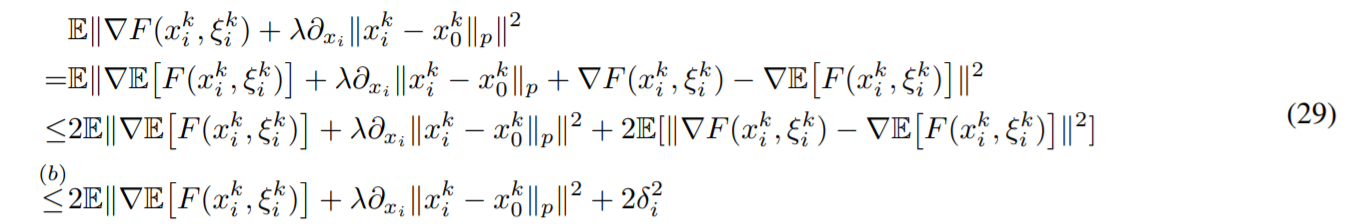
得到这样之后，虽然跟\(\nabla E[F(x_i^k, \xi_i^k)]\)与样本没有关系了但是形式上基本没有改变。仍然要分离\(\nabla E[F(x_i^k, \xi_i^k)]\)和\(\lambda \partial_{x_i} \Vert x_i^k-x_0^k\Vert_p\)，引入\(E[\nabla F(x_i^*, \xi_i^k)]+\lambda \partial_{x_i} \Vert x_i^*-x_0^*\Vert_p=0\)得到

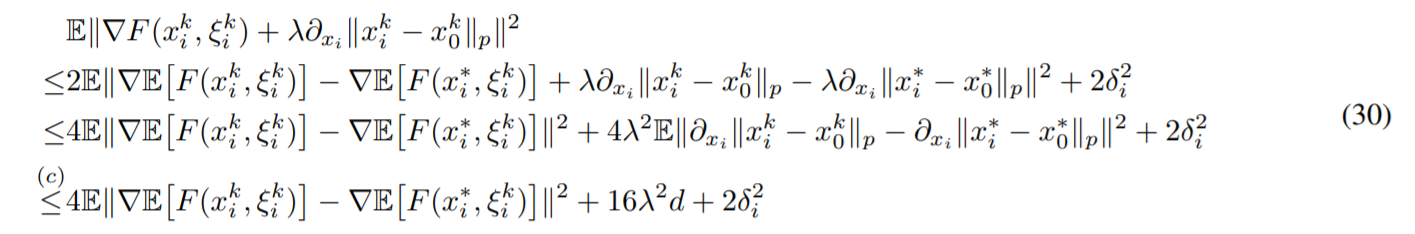
其中最后一个不等式用到了Proposition 1，即次梯度\(z\)满足\(\Vert z \Vert_b\leq 1\)。

再对\(C\)项进行放缩，在对这一项进行放缩时看形势可以用到\(L\) smooth或者\(\mu\) strongly convex的假设，在进行缩放时，先进行拆分，变为

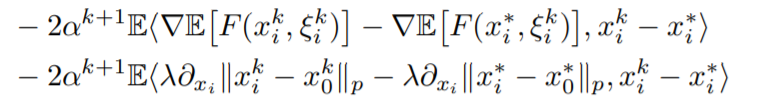
然后可以再利用^[2]中p66中的定理，可以得到

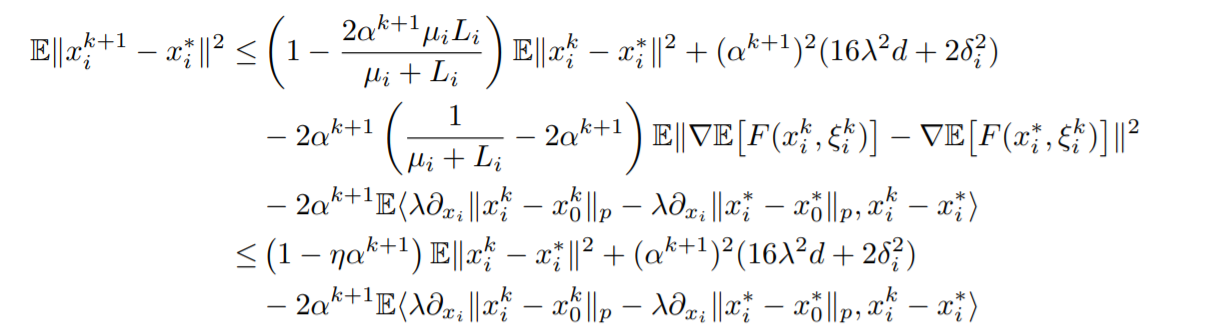
其中第二个不等式通过了对学习率\(\alpha\)的限制得到。化简结果中第一项是我们要保留的，第二项是一个误差，第三项还需要进行再次处理。

现在转向server端的参数更新，证明方式大同小异，

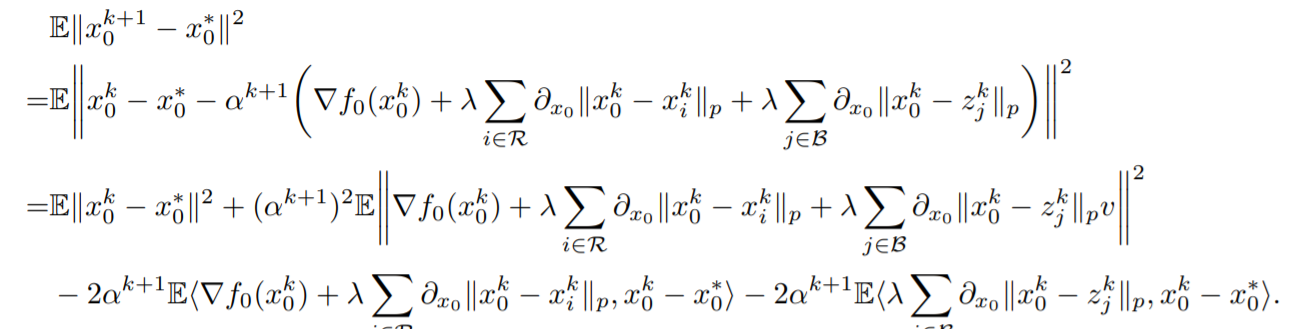
同样将更新规则带入整理得到四项，对于第二项和第三项，与regular worker不同，要将Byzantine的client去除掉，再利用同样的缩放技巧。对于第四项，则直接利用AM-GM inequality可以得到

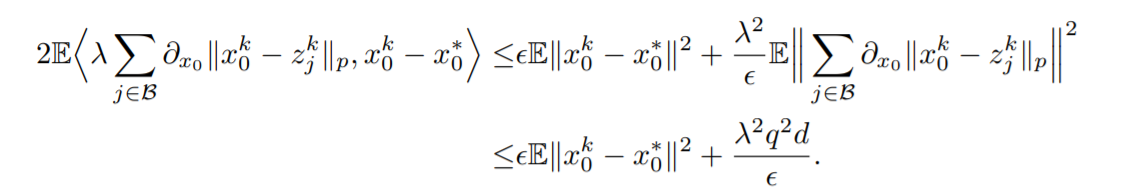
server的式子缩放整理可以得到

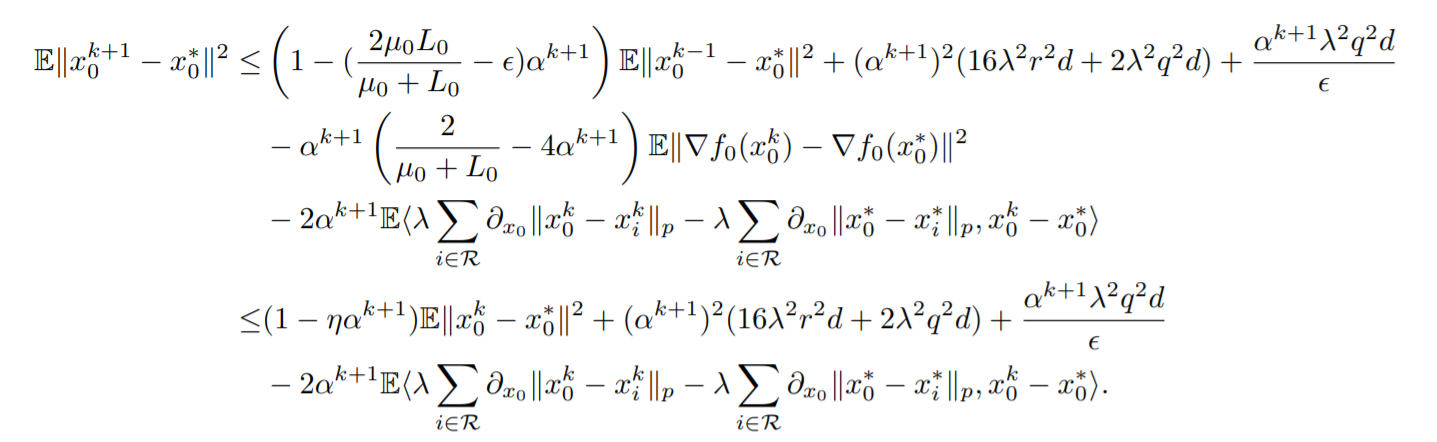
无论是client还是server最后的式子中都有一个\(\E<\lambda\sum\limits_{i\in\mathcal{R}}\partial_{x}\Vert x^k_0 - x^k_i\Vert_p-\lambda\sum\limits_{i\in\mathcal{R}}\partial_x\Vert x_0^*-x_i*\Vert, x^k-x^*>\)的东西，作者证明了这个东西是大于\(0\)的，减去一个大于\(0\)的项直接进行舍弃就放大了。作者设计了如下函数，通过\(g(x)\)是凸函数证明了这件事情

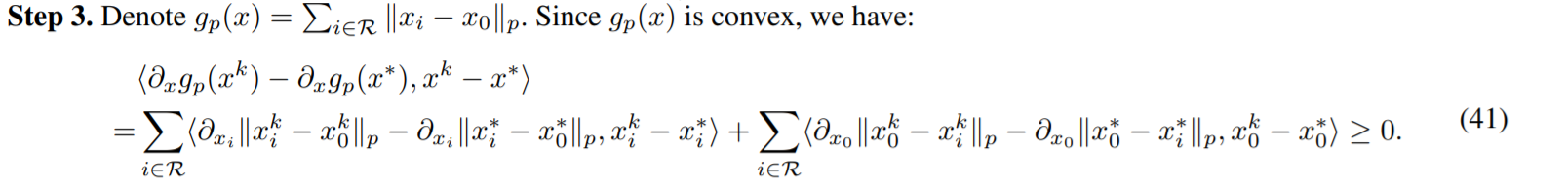
最终得到的结果就是下面这个样子

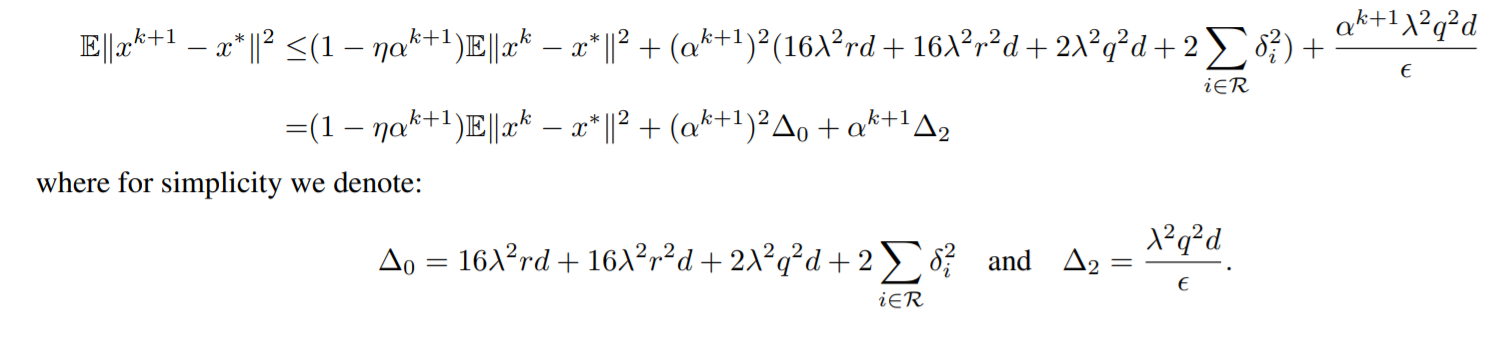
作者在这里讨论了学习率\(\aplha\)是固定值还是跟随步数逐渐缩小的值，至于为什么学习率要减小呢，可以看看SVRG(Stochasitc Variance Reduce Gradient)^[3]。如果是采用固定学习率的话，那么直接可以telescopic cancellation就可以得到，如果是随着步数变化的学习率的话（一般是\(\frac{\alpha}{t+1}\)这种形式），就需要通过数学归纳法来进行了。

文章最后说的\(\frac{1}{\sqrt{k}}\)函数值收敛好吧，根据convex和\(\mu\) strongly convex一转化应该就OK了。

总结和心得

作者这样formula给个性化的参数提供了另一种思路，但是个性化和全局最优的\(w^*\)到底存在什么联系还需要进一步探究。
收敛性证明的格式基本如上所示，常用到AM-GM，holder-inequality，\(\Vert a-b\Vert^2 \leq 2 \Vert a\Vert^2 + 2\Vert b\Vert^2\)，在证明中会用到学习率\(\eta\)的条件来消除某些不好处理的项。如果学习率是变动的那么则要使用归纳法。