HMM
模型结构
隐马尔科夫模型如下图所示,
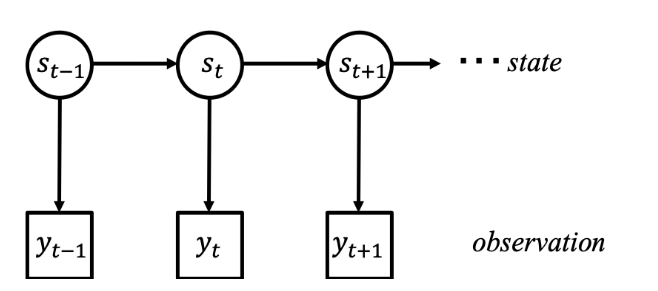
\(s\)我们是无法直接观测到的,我们得到的是对state的一种度量,记为\(y\)。模型涉及两个部分:一个是从\(s_{t-1}\to s_t\)的转移,另一个是\(s_t\to y_t\)由state生成观测变量\(y\)的部分。
HMM主要涉及以下三个问题:
- 在已知\(s_{t-1}\to s_t\)和\(s_{t}\to y_t\)两个分布的情况下计算\(P(X)\),即似然
- 根据得到的观测数据计算\(s_{t-1}\to s_t\)和\(s_{t}\to y_t\)两个分布的模型参数
- 预测,即已知模型分布参数和观测数据情况下,推测对应的state信息
文章基本是参考资料[1]的概括和代码的简化整理。
似然计算
如果直接用\(P(X)=\sum\limits_Z P(X,Z)\)来计算的话,时间复杂度大约是\(O(N^T)\),其中\(X\)表示观测变量,\(Z\)表示隐变量,N表示\(Z\)的可能取值,\(T\)表示时间长度。
一般都会用\(\alpha-\beta\)算法来简化计算,\(\alpha,\beta\)定义如下
\[\begin{align*}
\alpha_t &= P(X_{1:t},Z_t)\\
\beta_t &= P(X_{t+1:N}\vert Z_t)
\end{align*}
\]
可以看到\(\sum\limits_{Z_t=i}\alpha_t\times\beta_t=P(X)\)
\(\alpha_t\)和\(\beta_t\)的递推关系如下
\[\begin{align*}
\alpha_t &= \sum_{z_{t-1}} \alpha_{t-1} P(Z_t\vert Z_{t-1}) P(X_t\vert Z_t)\\
\beta_t & =\sum_{z_{t+1}} \beta_{t+1} P(Z_{t+1}\vert Z_t)P(X_{t+1}\vert Z_{t+1})
\end{align*}
\]
可以看到\(\alpha\)是从前往后,而\(\beta\)是从后往前,这样给定初始值的情况下,就可以计算下去。
\[\begin{align*}
\alpha_0 &= \pi_0 * P(X_0\vert Z_0) \\
\beta_N &= \bold 1
\end{align*}
\]
代码如下:
def evaluate_alpha(self, X):
'''
alpha_t = P(X_{1:t}, s_t)
:param X: observed list
:return: likelihood of X given parameters
'''
alpha = self.pi * self.B[:, X[0]]
for t in range(1, len(X)):
alpha = np.sum(alpha.reshape(-1, 1) * self.A, axis=0) * self.B[:, X[t]]
return alpha.sum()
def evaluate_beta(self, X):
'''
beta_t = P(X_{t+1:N} | s_t)
:param X: observed list
:return: beta_1
'''
beta = np.ones(self.N)
for t in X[:0:-1]:
beta = np.sum(self.A * beta * self.B[:, t], axis=1)
return np.sum(beta * self.pi * self.B[:, X[0]])
参数推断
关于参数推断部分,套用\(EM\)框架,再利用Lagrange即可,详细步骤可以查阅参考资料[1],参数更新公式如下
\[\begin{align*}
\pi_i^{t+1} &= \frac{\alpha_1(i)\beta_1(i)}{P(X\vert)} \\
a_{i,j}&= \frac{\sum_{t=1}^{T-1}a_t(i)\beta_{t+1}(j)a_{i,j}b_j(x_{t+1})}{\sum_{t=1}^{T-1}\alpha_t(i)\beta_t(i)}\\
b_{j,k}&=\frac{\sum_{t=1}^T\alpha_t(j)\beta_t(j)I(x_t=k)}{\sum_{t=1}^T \alpha_t(j)\beta_t(j)}
\end{align*}
\]
文章代码里关于\(\beta\)的更新是element-wise的形式,其实可以写成向量形式的。推断部分的代码如下
def fit(self, X):
'''
learn parameter
:param X: observed list
:return: updated parameter
'''
self.pi = np.random.rand(self.N)
self.pi = self.pi / self.pi.sum()
self.A = np.ones((self.N, self.N)) / self.N
self.B = np.ones((self.N, self.M)) / self.M
T = len(X)
for _ in range(50):
alpha, beta = self.alpha_beta(X)
gamma = alpha * beta
# update A
for i in range(self.N):
for j in range(self.N):
self.A[i, j] = np.sum(alpha[:-1, i] * beta[1:, j] * self.A[i, j] * self.B[j, X[1:]]) / gamma[:-1, i].sum()
# update B
for i in range(self.N):
for j in range(self.M):
self.B[i, j] = np.sum(gamma[:, i] * (X == j)) / gamma[:, i].sum()
self.pi = (alpha[0] * beta[0]) / np.sum(alpha[0] * beta[0])
def alpha_beta(self, X):
T = len(X)
alpha = np.zeros((T, self.N))
beta = np.ones((T, self.N))
alpha[0, :] = self.pi * self.B[:, X[0]]
for t in range(1, T):
alpha[t, :] = np.sum(alpha[t-1, :].reshape(-1, 1) * self.A, axis=0) * self.B[:, X[t]]
for t in range(T-1, 0, -1):
beta[t-1, :] = np.sum(self.A * beta[t, :] * self.B[:, X[t]], axis=1)
return (alpha, beta)
预测
在预测state状态时,要计算全概率\(P(X,Z)\)的概率,代码如下
def decode(self, X):
'''
:param X: observation list
:return: hidden state list
'''
T = len(X)
x = X[0]
delta = self.pi * self.B[:,x]
varphi = np.zeros((T, self.N), dtype=int)
path = [0] * T
for i in range(1, T):
delta = delta.reshape(-1,1) # 转成一列方便广播
tmp = delta * self.A
varphi[i,:] = np.argmax(tmp, axis=0)
delta = np.max(tmp, axis=0) * self.B[:,X[i]]
path[-1] = np.argmax(delta)
# 回溯最优路径
for i in range(T-1,0,-1):
path[i-1] = varphi[i, path[i]]
return path
全部代码如下
import os
import numpy as np
class HMM():
def __init__(self, N, M, pi=None, A=None, B=None):
self.N = N
self.M = M
self.pi = pi
self.A = A
self.B = B
def get_data_with_distribution(self, dist):
'''
:param dist: distribution of data
:return: sample index of the distribution
'''
r = np.random.rand()
assert type(r) is not np.ndarray
for i, p in enumerate(dist):
print(r, p)
if r < p:
return i
else:
r -= p
def generate(self, T:int):
'''
:param T: number of samples
:return: simulated dataset
'''
z = self.get_data_with_distribution(self.pi) # state
x = self.get_data_with_distribution(self.B[z]) # observation
result = [x]
for _ in range(T-1):
z = self.get_data_with_distribution(self.A[z]) # next state
x = self.get_data_with_distribution(self.B[z]) # next observation
result.append(x)
return result
def evaluate_alpha(self, X):
'''
alpha_t = P(X_{1:t}, s_t)
:param X: observed list
:return: likelihood of X given parameters
'''
alpha = self.pi * self.B[:, X[0]]
for t in range(1, len(X)):
alpha = np.sum(alpha.reshape(-1, 1) * self.A, axis=0) * self.B[:, X[t]]
return alpha.sum()
def evaluate_beta(self, X):
'''
beta_t = P(X_{t+1:N} | s_t)
:param X: observed list
:return: beta_1
'''
beta = np.ones(self.N)
for t in X[:0:-1]:
beta = np.sum(self.A * beta * self.B[:, t], axis=1)
return np.sum(beta * self.pi * self.B[:, X[0]])
def fit(self, X):
'''
learn parameter
:param X: observed list
:return: updated parameter
'''
self.pi = np.random.rand(self.N)
self.pi = self.pi / self.pi.sum()
print(self.pi)
self.A = np.ones((self.N, self.N)) / self.N
self.B = np.ones((self.N, self.M)) / self.M
T = len(X)
for _ in range(50):
alpha, beta = self.alpha_beta(X)
gamma = alpha * beta
# update A
for i in range(self.N):
for j in range(self.N):
self.A[i, j] = np.sum(alpha[:-1, i] * beta[1:, j] * self.A[i, j] * self.B[j, X[1:]]) / gamma[:-1, i].sum()
# update B
for i in range(self.N):
for j in range(self.M):
self.B[i, j] = np.sum(gamma[:, i] * (X == j)) / gamma[:, i].sum()
self.pi = (alpha[0] * beta[0]) / np.sum(alpha[0] * beta[0])
def alpha_beta(self, X):
T = len(X)
alpha = np.zeros((T, self.N))
beta = np.ones((T, self.N))
alpha[0, :] = self.pi * self.B[:, X[0]]
for t in range(1, T):
alpha[t, :] = np.sum(alpha[t-1, :].reshape(-1, 1) * self.A, axis=0) * self.B[:, X[t]]
for t in range(T-1, 0, -1):
beta[t-1, :] = np.sum(self.A * beta[t, :] * self.B[:, X[t]], axis=1)
return (alpha, beta)
def decode(self, X):
'''
:param X:
:return:
'''
T = len(X)
x = X[0]
delta = self.pi * self.B[:,x]
varphi = np.zeros((T, self.N), dtype=int)
path = [0] * T
for i in range(1, T):
delta = delta.reshape(-1,1) # 转成一列方便广播
tmp = delta * self.A
varphi[i,:] = np.argmax(tmp, axis=0)
delta = np.max(tmp, axis=0) * self.B[:,X[i]]
path[-1] = np.argmax(delta)
# 回溯最优路径
for i in range(T-1,0,-1):
path[i-1] = varphi[i, path[i]]
return path
if __name__ == "__main__":
import matplotlib.pyplot as plt
def triangle_data(T): # 生成三角波形状的序列
data = []
for x in range(T):
x = x % 6
data.append(x if x <= 3 else 6 - x)
return data
data = np.array(triangle_data(30))
hmm = HMM(10, 4)
hmm.fit(data) # 先根据给定数据反推参数
gen_obs = hmm.generate(30) # 再根据学习的参数生成数据
x = np.arange(30)
plt.scatter(x, gen_obs, marker='*', color='r')
plt.plot(x, data, color='g')
plt.show()


 浙公网安备 33010602011771号
浙公网安备 33010602011771号