含有分类变量（categorical variable）的逻辑回归（logistic regression）中虚拟变量（哑变量，dummy variable）的理解
使用R语言做逻辑回归的时候，当自变量中有分类变量（大于两个）的时候，对于回归模型的结果有一点困惑，搜索相关知识发现不少人也有相同的疑问，通过查阅资料这里给出自己的理解。
首先看一个实例（数据下载自：http://freakonometrics.free.fr/db.txt）
> db <- read.table("db.txt",header=TRUE,sep=";")
> head(db)
Y X1 X2 X3 1 1 3.297569 16.25411 B 2 1 6.418031 18.45130 D 3 1 5.279068 16.61806 B 4 1 5.539834 19.72158 C 5 1 4.123464 18.38634 C 6 1 7.778443 19.58338 C
> summary(db)
Y X1 X2 X3 Min. :0.000 Min. :-1.229 Min. :10.93 A:197 1st Qu.:1.000 1st Qu.: 4.545 1st Qu.:17.98 B:206 Median :1.000 Median : 5.982 Median :20.00 C:196 Mean :0.921 Mean : 5.958 Mean :19.94 D:197 3rd Qu.:1.000 3rd Qu.: 7.358 3rd Qu.:21.89 E:204 Max. :1.000 Max. :11.966 Max. :28.71
> reg <- glm(Y~X1+X2+X3,family=binomial,data=db)
> summary(reg)
Call: glm(formula = Y ~ X1 + X2 + X3, family = binomial, data = db) Deviance Residuals: Min 1Q Median 3Q Max -2.98017 0.09327 0.19106 0.37000 1.50646 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -4.45885 1.04646 -4.261 2.04e-05 *** X1 0.51664 0.11178 4.622 3.80e-06 *** X2 0.21008 0.07247 2.899 0.003745 ** X3B 1.74496 0.49952 3.493 0.000477 *** X3C -0.03470 0.35691 -0.097 0.922543 X3D 0.08004 0.34916 0.229 0.818672 X3E 2.21966 0.56475 3.930 8.48e-05 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 552.64 on 999 degrees of freedom Residual deviance: 397.69 on 993 degrees of freedom AIC: 411.69 Number of Fisher Scoring iterations: 7
该数据集三个自变量中 X1， X2为连续型变量，X3为分类变量（A,B,C,D,E）。 获取逻辑回归结果时发现X3变量的表示形式和X1，X2不一样，并且分别产生了X3B, X3C, X3D, X3E四个新的变量，但是又没有X3A变量。后来查阅相关资料才明白原来逻辑回归中处理分类变量和连续型变量是不一样的。
当分类自变量的类别大于两个的时候，需要建立一组虚拟变量（哑变量）来代表变量的归属性质。一般虚拟变量的数目比分类变量的数目少一个，少掉的那个就作为参照类（reference category）。例如本例中，A就是参照类，X3B, X3C, X3D, X3E就是四个虚拟变量。参照类的选取是随意的，R语言逻辑回归默认将分类变量的第一个factor设置为虚拟变量。此时的回归模型如下：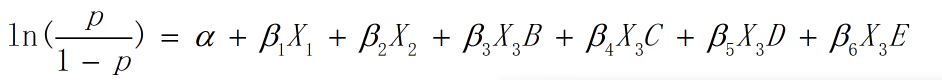
四个虚拟变量的取值为1或0，即当观测值中的分类变量属于某一组时，该组的虚拟变量值为1，剩下的虚拟变量值为0。
例如，当一组观测值（X1，X2，X3，Y）中 X3 的值为B时，虚拟变量X3B = 1， X3C, X3D, X3E 都为0，此时：
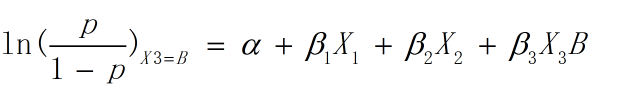
而当一组观测值（X1，X2，X3，Y）中 X3 的值为A时， 因为A为参照类，所以此时X3B, X3C, X3D, X3E都为0，此时：
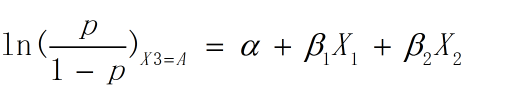
因此在控制变量条件下，即假设两组观测值中，X1， X2相同，而X3分别为A和B， 由上面两式相减可得：
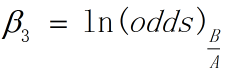
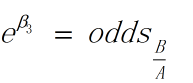
此处odds(B/A)为变量B对变量A的发生比率，即变量B的发生比与变量A的发生比的比值。大于1的发生比率表明事件发生的可能性会提高，或者说自变量对事件发生的概率有正的作用。例如，假如说odds(B/A)的数值大于1，那么说明在X1，X2不变的条件下，X3取值B比X3取值A有更大的概率使Y的值为1。（王济川，郭志刚. Logistic 回归模型 —— 方法与应用[M]. 北京：高等教育出版社）
回到开头的例子，根据结果我们得以得出这样的结论，变量X3取值A,C,D对Y的影响差不多，而变量X3取值B,E会使得Y取值为1的概率比去A,C,D显著增大。简单看一下：
> db_a <- db[db$X3 == "A",] > db_b <- db[db$X3 == "B",] > db_c <- db[db$X3 == "C",] > db_d <- db[db$X3 == "D",] > db_e <- db[db$X3 == "E",] > table(db_a$Y) 0 1 25 172 > table(db_b$Y) 0 1 6 200 > table(db_c$Y) 0 1 21 175 > table(db_d$Y) 0 1 22 175 > table(db_e$Y) 0 1 5 199
大致从结果看出确实变量B,E组的Y值为1的比例要高于A,C,D组。
我们也可以自己定义虚拟变量：
> levels(db$X3) [1] "A" "B" "C" "D" "E" > db$X3 <- relevel(db$X3, "B") > levels(db$X3) [1] "B" "A" "C" "D" "E"
同上面的回归模型：
> reg <- glm(Y~X1+X2+X3,family=binomial,data=db) > summary(reg) Call: glm(formula = Y ~ X1 + X2 + X3, family = binomial, data = db) Deviance Residuals: Min 1Q Median 3Q Max -2.98017 0.09327 0.19106 0.37000 1.50646 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) -2.71389 1.07274 -2.530 0.011410 * X1 0.51664 0.11178 4.622 3.8e-06 *** X2 0.21008 0.07247 2.899 0.003745 ** X3A -1.74496 0.49952 -3.493 0.000477 *** X3C -1.77966 0.51002 -3.489 0.000484 *** X3D -1.66492 0.50365 -3.306 0.000947 *** X3E 0.47470 0.66354 0.715 0.474364 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 (Dispersion parameter for binomial family taken to be 1) Null deviance: 552.64 on 999 degrees of freedom Residual deviance: 397.69 on 993 degrees of freedom AIC: 411.69 Number of Fisher Scoring iterations: 7
主要内容就这么多，如果想要更详细的了解可以参考：王济川，郭志刚. Logistic 回归模型 —— 方法与应用[M]. 北京：高等教育出版社
以及链接：https://www.r-bloggers.com/logistic-regression-and-categorical-covariates/
版权声明：本文为博主原创文章，博客地址：http://www.cnblogs.com/Demo1589/p/8973731.html，转载请注明出处。
