[CF737E] Tanya is 5！

Tanya is 5！

题意

有 \(n\) 个孩子，\(m\) 种机器，\(b\) 块钱。一开始，每种机器只有一个，但每种机器你有且仅有一次机会花 \(p_i\) 块再购买一台。第 \(i\) 个孩子想在第 \(j\) 种机器上工作 \(C_{i,j}\) 时间，工作可以中断，工作时间累加。孩子可以不花费时间中断工作和跑去另一个机器工作。每个时刻一个孩子只能在一台机器上工作，每台机器于同一时刻只能被一个孩子工作。

求完成所有工作的最少时间，并输出工作的方案。注意，你可以任意花费钱，只要在 \(b\) 块以内。

\(n\leq 40,1\leq m\leq 10,0\leq b\leq 10^6,1\leq p_i \leq10^6,0\leq C_{i,j} \leq 2500\)

分析

首先我们考虑没有购买机器的机会我们可以怎么做。

设 \(T_j = \sum_i C_{i,j},S_i = \sum_j = C_{i,j}\)，其中 \(S_i\) 表示第 \(i\) 个孩子希望工作的总时间，\(T_j\) 表示第 \(j\) 台机器需要被工作的总时间。显然，我们答案一个显然的下界为 \(max(max\{ T_j\},max\{ S_i\})\)，设为 \(X\)。

那么我们证明 \(X\) 是可以被取得的。

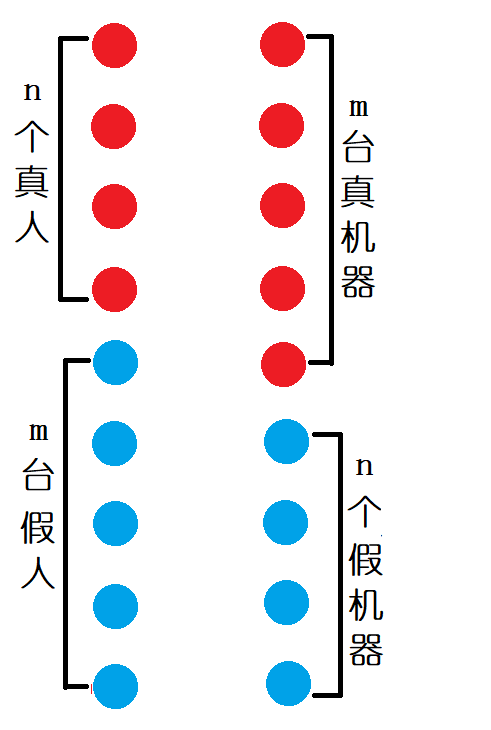
考虑建二分图，人为左部节点，机器为右部节点。

对于每个人，我们建一个对应的假机器，对于每个机器，我们建一个对应的假人。

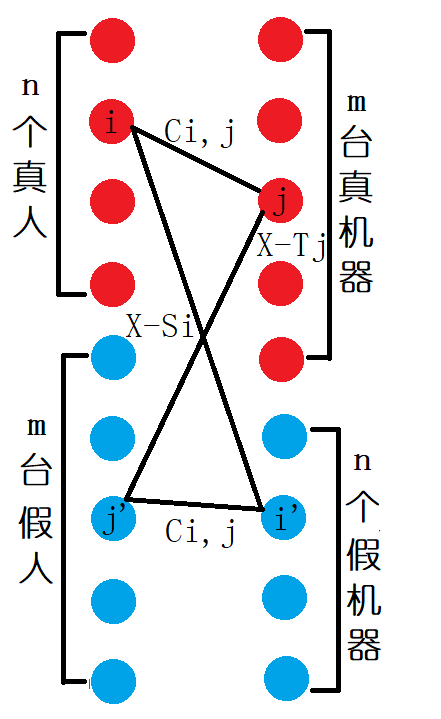
• 对于第 \(i\) 个真人和第 \(j\) 个真机器，连边权值为 \(C_{i,j}\)。

• 对于第 \(i\) 个真人和第 \(j\) 个假机器，连边权值为 \(X - S_i\)。

• 对于第 \(j\) 个假人和第 \(j\) 个真机器，连边权值为 \(X - T_j\)。

• 对于第 \(j\) 个假人和第 \(i\) 个假机器，连边权值为 \(C_{i,j}\)。

这个时候，能够发现二分图两边的节点数量相同，且每个点度数都是 \(X\)。根据 \(Hall\) 定理，显然该图可以分解为 \(X\) 个完美匹配，每一次找出一个匹配，我们就能够取到 \(X\)。

事实上，假人和假机器的作用只在于补充度数，每一次匹配中，如果真人匹配真机器，说明这个时刻该人在这台机器上工作，否则说明人或者机器轮空。

考虑怎么购买机器可以让决策更优。

注意到我们的下界只和 \(S_i\) 和 \(T_j\) 有关，显然，购买机器只能够影响到 \(T_j\)，我们每次复制机器，相当于把某个 \(T_j\) 分成两份 \(\lceil \frac{T_j}{2}\rceil\)，\(\lfloor \frac{T_j}{2}\rfloor\)，那我们只需要尽量把最大的买了即可。

CODE

#include <bits/stdc++.h>
using namespace std;
const int N = 50, M = 1e6 + 10, K = 1e5 + 10;
inline int read()
{
	int s = 0, w = 1;
	char ch = getchar();
	while(ch < '0' || ch > '9') { if(ch == '-') w *= -1; ch = getchar(); }
	while(ch >= '0' && ch <= '9') s = s * 10 + ch - '0', ch = getchar();
	return s * w;
}
struct node{ int p, id; }ch[N];
struct edge{
	int u, v;
}e[M];
int n, m, b, tot, ans, cnt;
int id[2 * N], pos[N], sum[N], col[M];
int R[N], Z[N], c[N][N], match[2 * N][K];
bool buy[N];
set<int> s[2 * N];
inline bool cmp1(node x, node y) { return Z[x.id] > Z[y.id]; }
inline bool cmp2(node x, node y) { return x.id < y.id; }
inline void dfs(int u, int x, int y)
{
	int id = match[u][x], v = (e[id].u == u ? e[id].v : e[id].u);
	match[u][x] = match[v][x] = 0;
	if(match[v][y]) dfs(v, y, x);
	else s[v].insert(x), s[v].erase(y);
	match[v][y] = match[u][y] = id, col[id] = y;
}
int main()
{
	n = read(), m = read(), b = read();
	for(register int i = 1; i <= m; i++) ch[i].p = read(), ch[i].id = i;
	for(register int i = 1; i <= n; i++){
		int x = read();
		for(register int j = 1, y; j <= x; j++) y = read(), c[i][y] = read();
	}
	for(register int i = 1; i <= n; i++)
		for(register int j = 1; j <= m; j++) R[i] += c[i][j], Z[j] += c[i][j];
	for(register int i = 1; i <= n; i++) ans = max(ans, R[i]);
	sort(ch + 1, ch + m + 1, cmp1);
	for(register int i = 1; i <= m; i++)
		if(ch[i].p <= b) b -= ch[i].p, buy[ch[i].id] = true;
	for(register int i = 1; i <= m; i++)
		ans = max(ans, buy[i] ? (Z[i] + 1) / 2 : Z[i]);
	for(register int i = 1; i <= m; i++){
		pos[i] = ++tot, id[tot] = i;
		if(buy[i]) id[++tot] = i;
	}
	sort(ch + 1, ch + m + 1, cmp2);
	for(register int i = 1; i <= n; i++){
		for(register int j = 1; j <= m; j++){
			while(c[i][j]--){
				sum[j]++;
				if(!buy[j]) e[++cnt] = (edge){i, pos[j] + n};
				else if(sum[j] <= Z[j] / 2) e[++cnt] = (edge){i, pos[j] + n};
				else e[++cnt] = (edge){i, pos[j] + 1 + n}; //第二个点连边 
			}
		}
	}
	for(register int i = 1; i <= n + tot; i++)
		for(register int j = 1; j <= ans; j++) s[i].insert(j);
	for(register int i = 1; i <= cnt; i++){
		int u = e[i].u, v = e[i].v, c1 = *s[u].begin(), c2 = *s[v].begin();
		if(match[v][c1]) dfs(v, c1, c2), s[v].erase(c2);
		match[u][c1] = match[v][c1] = i, col[i] = c1;
		s[u].erase(c1), s[v].erase(c1);
	}
	cout << ans << "\n";
	for(register int i = 1; i <= m; i++) printf("%d", buy[i]);
	puts("");
	cout << cnt << "\n";
	for(register int i = 1; i <= cnt; i++) printf("%d %d %d 1\n", e[i].u, id[e[i].v - n], col[i] - 1);
	return 0;
}