浅谈圆方树
浅谈圆方树
点双连通分量
定义
若一个无向图中,去掉任意一个节点都不会改变此图的连通性,即不存在割点,则称作点双连通图。
一个无向图中的每个极大点双连通子图称作此无向图的点双连通分量。
与强连通分量等不同,一个点可能属于多个点双,但是一条边属于恰好一个点双。
所以,我们标记点双连通分量常常是标记边。
在圆方树中的一些变化
-
定义近似:不存在割点的图。
-
不同点:对于一个两个点一条边的子图。按照最开始我们的定义,他不是一个点双,但在这里,我们认为他是一个点双。
-
注意:使用后面的定义仍然有一个点可能属于多个点双,但一条边只属于恰好一个点双的性质。
圆方树
定义
-
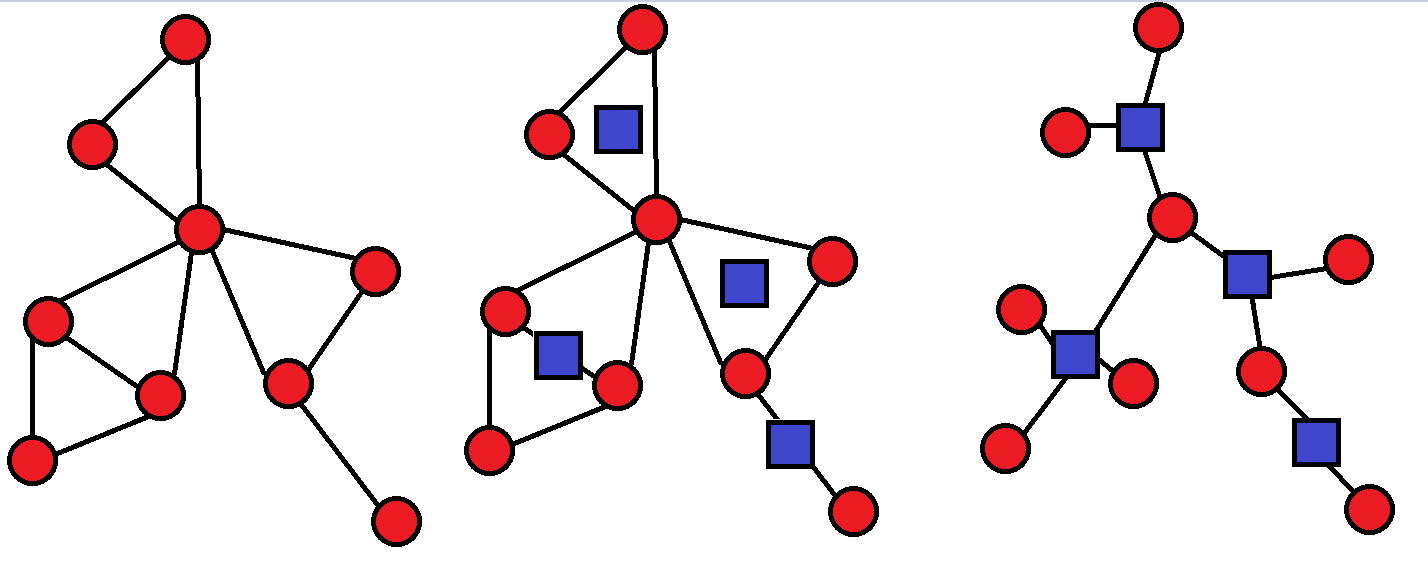
原图中所有的点被称为圆点。
-
对于每个点双连通分量:
- 删去这个点双内部所有边。
- 建立一个新的方点。
- 方点向所有点双中的点连边。
-
所以对于圆方树,一共有 \(n + c\) 个点,其中 \(n\) 是原图点数, \(c\) 是原图点双连通分量的数量。
-
基本性质:圆方树中每条边连接一个圆点和一个方点。
-
具体可参考下图:
-
圆方树的点数小于 \(2n\)。因为割点的数量小于 \(n\) 。
-
注意:如果原图连通,圆方树才是一棵树,否则,他是一个森林。
构建
构建圆方树使用到的算法是 \(tarjan\) 算法,我们用 \(dfn[u]\) 储存节点 \(u\) 的 \(DFS\) 序,即第一次访问到 \(u\) 时它是第几个被访问到的节点。 \(low[u]\) 储存的是节点 \(u\) 的 \(DFS\) 树中的子树中的某个点 \(v\) 通过最多一次返祖边或向父亲的树边能访问到的点的最小 \(DFS\) 序。
容易注意到其与正常 \(tarjan\) 的区别在于是否能够通过树边进行更新。
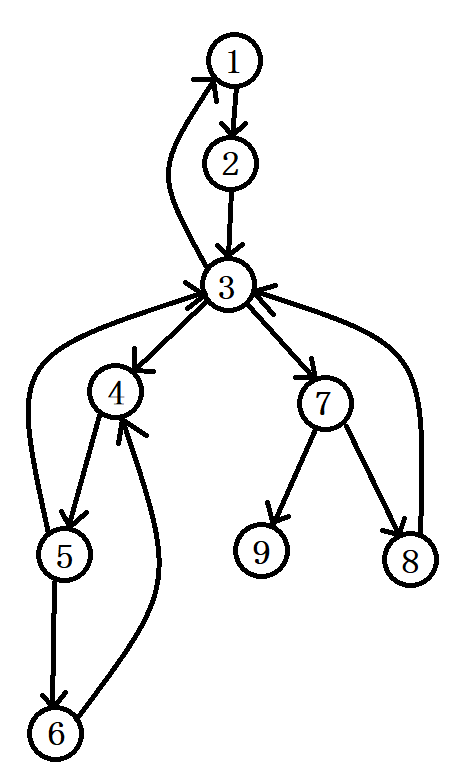
| u | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| low[u] | 1 | 1 | 1 | 3 | 3 | 4 | 3 | 3 | 7 |
容易注意到 \(9\) 所对应的 \(low\) 值即和正常 \(tarjan\) 不同的具体体现。
下为正常 \(tarjan\) 的代码:
inline void Tarjan(int u, int fa)
{
low[u] = dfn[u] = ++t;
//low 初始化为当前节点 dfn
for(register int v : G[u]){
if(!dfn[v]){ //如果没有访问过
Tarjan(v); //递归
low[u] = min(low[u], low[v]);
}
else if(v != fa) low[u] = min(low[u], dfn[v]);
}
}
下为圆方树中 \(tarjan\) 的代码:
inline void Tarjan(int u)
{
low[u] = dfn[u] = ++t;
//low 初始化为当前节点 dfn
for(register int v : G[u]){
if(!dfn[v]){ //如果没有访问过
Tarjan(v); //递归
low[u] = min(low[u], low[v]);
}
else low[u] = min(low[u], dfn[v]);
}
}
到这里,我们学会了如何建立一棵圆方树。
接下来是一些例题。
[APIO2018] 铁人两项
题意
给定一张简单无向图,问有多少对三元组 \(<s,c,f>\) (\(s,c,f\)互不相同),使得存在一条简单路径从 \(s\) 出发,经过 \(c\) 到达 \(f\)。
Sol
-
点双的性质:对于一个点双中的两点,它们之间简单路径的并集恰好完全等于这个点双。即同一个点双中的不同点 \(u,v\) 之间一定存在一条简单路径经过给定的在同一个点双内的另一点 \(w\) 。
-
这个性质告诉我们,考虑两圆点在圆方树上的路径,与路径上经过的方点相邻的圆点的集合,就等于原图中两点简单路径上的点集。
-
这促使我们想到固定 \(s,f\) ,求合法的 \(c\) 的数量,显然有合法 \(c\) 的数量等于 \(s,f\) 之间简单路径并集的点数减去 \(2\)(即去掉 \(s,f\) 本身)。
-
于是我们考虑先构建出原图的圆方树,两点之间 \(c\) 的数量,就和它们在圆方树上经过的方点和圆点有关。我们考虑给方点和圆点赋上特定的值,即每个方点的权值为对应点双的大小,而每个圆点的权值为 \(-1\) 。
-
这样赋值后,两圆点间圆方树上路径权值和,恰好等于原图中简单路径的并集大小减 \(2\) 。这不难理解,途径每个方点统计到相邻圆点的权值,但是中间经过的圆点会被重复计算,减掉的 \(1\) 恰好抵消,而起点和终点不存在这种情况,所以我们多减掉了 \(2\) 。
-
到这里,进行树形 \(dp\) 即可。
-
总结:圆方树中,我们常常可以通过给点赋值来解决一些复杂的问题。
code
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 2e5 + 10;
inline int read()
{
int s = 0, w = 1;
char ch = getchar();
while(ch < '0' || ch > '9') { if(ch == '-') w *= -1; ch = getchar(); }
while(ch >= '0' && ch <= '9') s = s * 10 + ch - '0', ch = getchar();
return s * w;
}
int n, m, t, rec, cnt, top, ans;
int sck[N], dfn[N], low[N], siz[N], sum[N];
vector<int> G[N], T[N];
inline void Sol(int pos, int fa)
{
siz[pos] = pos <= rec;
for(register int v : T[pos])
if(v != fa) Sol(v, pos), siz[pos] += siz[v];
if(pos <= rec){
ans += (cnt - 1) * (cnt - 1);
for(register int v : T[pos])
if(v != fa) ans -= sum[v];
}
else{
for(register int v : T[pos])
if(v != fa) sum[pos] += siz[v] * siz[v];
int tem = (cnt - siz[pos]) * (cnt - siz[pos]);
for(register int v : T[pos])
if(v != fa) ans -= sum[pos] - siz[v] * siz[v] + tem;
}
}
inline void Tarjan(int pos)
{
sck[++top] = pos, cnt++;
dfn[pos] = low[pos] = ++t;
for(register int v : G[pos]){
if(!dfn[v]){
Tarjan(v), low[pos] = min(low[pos], low[v]);
if(low[v] == dfn[pos]){
int tem = 0; n++;
while(tem != v){
tem = sck[top--];
T[n].push_back(tem), T[tem].push_back(n);
}
T[n].push_back(pos), T[pos].push_back(n);
}
}
else low[pos] =min(low[pos], dfn[v]);
}
}
signed main()
{
n = read(), m = read(), rec = n;
for(register int i = 1; i <= m; i++){
int x = read(), y = read();
G[x].push_back(y), G[y].push_back(x);
}
for(register int i = 1; i <= rec; i++){
if(dfn[i]) continue;
cnt = 0, Tarjan(i), Sol(i, 0);
}
printf("%lld\n", ans);
return 0;
}
[CodeFoces 487E] Tourists
题意
给定一张简单无向连通图,要求支持两种操作:
-
修改一个点的点权。
-
询问两点之间所有简单路径上点权的最小值。
Sol
-
在学习完圆方树且看过上题之后,再来看这道题,很自然地,我们将有这样一个想法:对原图建出圆方树,给方点赋值赋上与它相连的所有圆点值中的最小值,之后在树链剖分加线段树套一套,这道题好像就做完了。
-
的确,如果没有操作 \(1\) 的话,我们确实可以简单地完成这道题目。但操作 \(1\) 的确是存在的,考虑这样一种极端情况,如果我每次修改一个圆点,我都会影响到与它相邻的所有方点,如果与它相邻的方点足够多,显然这样的复杂度我们是不能够接受的。
-
但很快我们又可以想到,既然与它相邻的方点太多,我们可以限制一下这个数量,即限制我们维护的信息。事实上,我们可以让每个圆点的值仅仅影响它的父亲,当然,根据圆方树的定义,它的父亲一定是个方点,发现这样做基本上不会影响到我们上述的过程,但是有效地解决了时间复杂度的问题,只需要注意在询问的时候,如果我们的 \(LCA\) 是方点,再将该方点的父亲圆点与我们的答案取 \(min\) 即可。
code
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 4e5 + 10, INF = 1e18;
inline int read()
{
int s = 0, w = 1;
char ch = getchar();
while(ch < '0' || ch > '9') { if(ch == '-') w *= -1; ch = getchar(); }
while(ch >= '0' && ch <= '9') s = s * 10 + ch - '0', ch = getchar();
return s * w;
}
int n, m, t, q, rec, cnt, tot;
int tr[4 * N];
int id[N], fa[N], dep[N], siz[N], top[N], son[N];
int arr[N], sck[N], dfn[N], low[N];
vector<int> G[N], T[N];
multiset<int> s[N];
//建立圆方树
inline void Tarjan(int pos)
{
sck[++tot] = pos, dfn[pos] = low[pos] = ++t;
for(register int v : G[pos]){
if(!dfn[v]){
Tarjan(v), low[pos] = min(low[pos], low[v]);
if(low[v] == dfn[pos]){
int tem = 0; n++;
while(tem != v){
tem = sck[tot--];
T[n].push_back(tem), T[tem].push_back(n);
}
T[n].push_back(pos), T[pos].push_back(n);
}
}
else low[pos] = min(low[pos], dfn[v]);
}
}
inline void dfs1(int u, int father)
{
fa[u] = father, dep[u] = dep[father] + 1, siz[u] = 1;
if(u <= rec && father) s[father].insert(arr[u]); //是圆点,只记录到父亲
for(register int v : T[u]){
if(v == father) continue;
dfs1(v, u);
siz[u] += siz[v];
if(siz[v] > siz[son[u]]) son[u] = v;
}
if(u > rec) arr[u] = *s[u].begin();
}
inline void dfs2(int u, int st)
{
top[u] = st, dfn[u] = ++cnt, id[cnt] = u;
if(son[u]) dfs2(son[u], st);
else return;
for(register int v : T[u])
if(v != fa[u] && v != son[u]) dfs2(v, v);
}
inline void update(int k) { tr[k] = min(tr[k << 1], tr[k << 1 | 1]); }
inline void build(int k, int l, int r)
{
if(l == r) { tr[k] = arr[id[l]]; return; }
int mid = (l + r) >> 1;
build(k << 1, l, mid), build(k << 1 | 1, mid + 1, r);
update(k);
}
inline void change(int k, int l, int r, int x, int v)
{
if(r < x || l > x) return;
if(l == r && l == x) { tr[k] = v; return; }
int mid = (l + r) >> 1;
change(k << 1, l, mid, x, v), change(k << 1 | 1, mid + 1, r, x, v);
update(k);
}
inline int ask(int k, int l, int r, int x, int y)
{
if(r < x || l > y) return INF;
if(l >= x && r <= y) return tr[k];
int mid = (l + r) >> 1;
return min(ask(k << 1, l, mid, x, y), ask(k << 1 | 1, mid + 1, r, x, y));
}
inline int query(int x, int y)
{
int res = INF;
while(top[x] != top[y]){
if(dep[top[x]] < dep[top[y]]) swap(x, y);
res = min(res, ask(1, 1, n, dfn[top[x]], dfn[x]));
x = fa[top[x]];
}
if(dep[x] < dep[y]) swap(x, y);
res = min(res, ask(1, 1, n, dfn[y], dfn[x]));
if(y > rec) res = min(res, arr[fa[y]]);
return res;
}
signed main()
{
n = read(), m = read(), q = read(), rec = n, arr[0] = INF;
for(register int i = 1; i <= n; i++) arr[i] = read();
for(register int i = 1; i <= m; i++){
int x = read(), y = read();
G[x].push_back(y), G[y].push_back(x);
}
Tarjan(1), dfs1(1, 0), dfs2(1, 1), build(1, 1, n);
while(q--){
char opt[10]; cin >> opt;
int a = read(), b = read();
if(opt[0] == 'C'){
if(fa[a]){
auto it = s[fa[a]].find(arr[a]); s[fa[a]].erase(it), s[fa[a]].insert(b);
arr[fa[a]] = *s[fa[a]].begin(), change(1, 1, n, dfn[fa[a]], arr[fa[a]]);
}
arr[a] = b, change(1, 1, n, dfn[a], b);
}
else printf("%lld\n", query(a, b));
}
return 0;
}



