[BZOJ4289] Tax [题解]

Tax

题面

给定一个 \(n\) 个点 \(m\) 条边的无向图，经过一个点的代价是进入和离开这个点的两条边的两条边的边权较大值，求从起点 \(1\) 到点 \(n\) 的最小代价。

起点的代价是离开起点的边的边权，终点的代价是进入终点的边的边权。

\(n\leq 1e5,m\leq 2e5\)

分析

最先想到的实际上是暴力，在 \(DJ\) 的状态上进一步记录了转移到当前状态的边权，从而进一步转移。

但很快我们会发现这不对，我们的边权具有后效性，不满足 \(DJ\) 从当前最小值转移必将得到下一个最小值的性质。

一时间好像没有了其它思路。

重新回到代价的定义，一个点的代价和路径上经过它的两条边有关，即与它相邻的一些边有关。

考虑把边转化成点。

一条无向边实际上对应的是两条有向边，也即对应两个点，在这两个点之间建立一条长度为边原长的边。

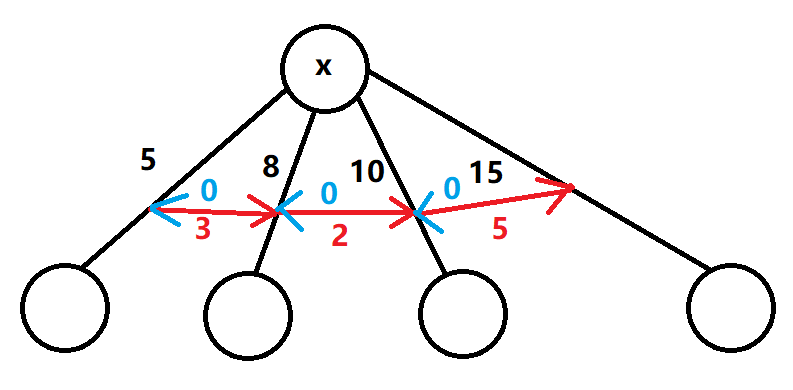
观察这幅图，对于每一个点 \(x\) ，我们将与它相连的边按照边权大小排序，边权小的边向第一个边权比它大的边连一条边权为它们权值差的有向边，再连接一条边权为 \(0\) 的反相边。

之后我们建立一个新的起始点 \(s\) ，一个新的终点 \(t\) ，\(s\) 与所有与 \(1\) 相连的边建立一条长度为此边原长的有向边，所有与 \(n\) 相连的边与 \(t\) 建立一条长度为 \(0\) 的有向边。

考虑这样建图为什么是对的，首先对于起点，我们前往任意一条边都将会花费一个初始代价，与题意相符，而我们的边在进入下一条边时，由于我们的代价是差值，对于小的边前往大的边，代价会很自然的变成较大值，而大的边前往小的边，代价为 \(0\) ，仍然为我们的大边。

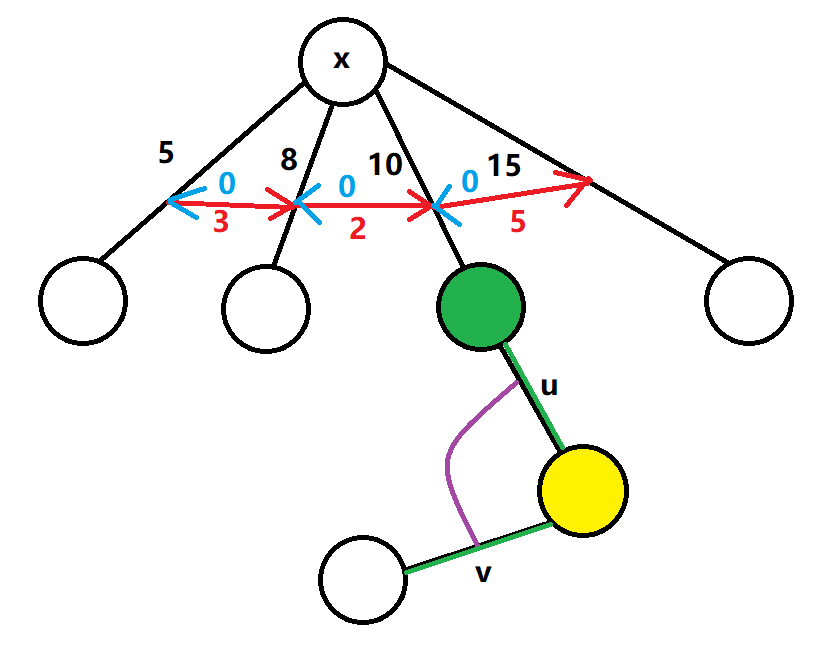
通过这样的连边，我们能够表示出每个点的代价，事实上，由于我们把初始的一条边拆成了两个点，当我们在进行如上图中 \(u\) 到 \(v\) 这类的转移时，相当于我们有一次切换，从由绿点散发出去的边转化成了从黄点散发出去的边，贡献的初始值还是我们的 \(u\) 。即等价于我们已经算出了绿点的代价，接下来我们正在计算的是通过黄点的代价。

这样，我们就巧妙的通过不停的这样转化，表示出了题目中的代价，跑一遍最短路即可。

CODE

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+10,M=2e5+10,P=2e6+10;
inline int read()
{
	int s=0,w=1;
	char ch=getchar();
	while(ch<'0'||ch>'9') { if(ch=='-') w*=-1; ch=getchar(); }
	while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
	return s*w;
}
struct Edge{ int v,w; };
struct BIT{ int id1,id2,val; }arr[M];
struct node{
	int p,val;
	bool operator <(const node &x)const{
		return val>x.val;
	}
};
int n,m,cnt,s,t;
int tot=-1,v[2*M],w[2*M],nex[2*M],first[N];
vector<Edge> vec[P];
inline void Add(int x,int y,int z)
{
	nex[++tot]=first[x];
	first[x]=tot;
	v[tot]=y,w[tot]=z;
}
inline bool cmp(BIT x,BIT y) { return x.val<y.val; }
int dis[P];
bool vis[P];
priority_queue<node> q;
inline void DJ()
{
	memset(dis,0x3f,sizeof(dis));
	dis[s]=0;
	q.push((node){s,0});
	while(!q.empty()){
		node now=q.top(); q.pop();
		if(vis[now.p]) continue;
		vis[now.p]=true;
		for(register int i=0;i<vec[now.p].size();i++){
			int to=vec[now.p][i].v,d=vec[now.p][i].w;
			//cout<<to<<endl; 
			if(dis[to]>dis[now.p]+d){
				dis[to]=dis[now.p]+d;
				q.push((node){to,dis[to]});
			}
		}
	}
}
signed main()
{
	memset(first,-1,sizeof(first));
	n=read(),m=read();
	for(register int i=1;i<=m;i++){
		int x=read(),y=read(),z=read();
		Add(x,y,z),Add(y,x,z); 
	}
	for(register int i=1;i<=n;i++){ //枚举起点 
		cnt=0;
		for(register int j=first[i];j!=-1;j=nex[j]){
			arr[++cnt].id1=j^1,arr[cnt].id2=j;
			arr[cnt].val=w[j];
		}
		sort(arr+1,arr+cnt+1,cmp);
		for(register int j=1;j<=cnt;j++){
			//cout<<
			vec[arr[j].id1].push_back((Edge){arr[j].id2,arr[j].val});
			if(j!=1) vec[arr[j].id2].push_back((Edge){arr[j-1].id2,0});
			if(j!=cnt) vec[arr[j].id2].push_back((Edge){arr[j+1].id2,arr[j+1].val-arr[j].val});
		}
	}
	s=tot+1,t=tot+2;
	for(register int i=first[1];i!=-1;i=nex[i]) vec[s].push_back((Edge){i,w[i]});
	for(register int i=first[n];i!=-1;i=nex[i]) vec[i].push_back((Edge){t,0});
	DJ();
	printf("%lld\n",dis[t]);
	return 0;
}