参天大树[题解]

参天大树

题目大意

给出一个 $n$ 层的满二叉树，其根节点编号为 $1$ ，对于每一个 $x(x \ge 1)$ ，编号为 $x$ 的节点有编号为 $2x$ 与编号为 $2x+1$ 的子节点。

需要从该二叉树的节点中选出一些节点(可以相同)，求出所有情况中他们 $LCA$ 的和。

则我们需要求出下面这个式子的值：

$$\sum_{i=1}^{i<=n}\sum_{j=1}^{j<=n} LCA(i,j)$$

最终答案对 $998244343$ 取模。

分析

拿到这个题，我们可以换一个角度来思考，不妨想一想如果我们想要选出节点的 $LCA$ 为 $i$ 节点，有多少种不同的情况。

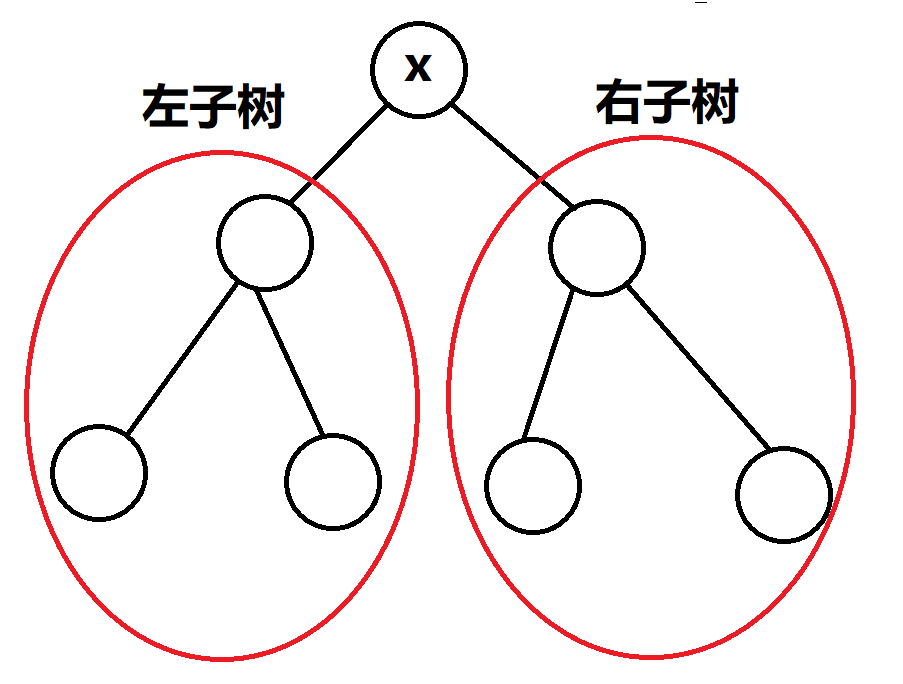
其实我们可以分为以下三种情况：

• 这两个点就是 $x$ 与 $x$ ，这样就能保证有 $x$ 的贡献，很显然该情况只会出现一次。

• 这两个点分别在 $x$ 的左子树与右子树，如上图，这样也能保证他们的 $LCA$ 恰为 $x$ ，则这种情况的总数肯定就是左子树的大小乘右子树的大小还要乘 $2$ ，注意这里的乘 $2$ 是因为除了选择同一个点的情况其余情况都可以反转。

• 固定其中一个点为 $x$ ，剩余的点在 $x$ 的子树中选取，则很显然情况数位 $2$ 乘 $x$ 所有后代的数量。

那么，我们就能处理出 $x$ 为 $LCA$ 时的所有贡献了。

设 $sum_{sun}$ 为 $x$ 一个子树的大小，设根节点的层数为 $1$ ， $x$ 的层数为 $i$ ，则易有 $sum_{sun}=2^{n-i}-1$ 。

则当前的可知道 $LCA$ 为 $x$ 的贡献为:

$$sum_x=x\times [1+2\times (2^{n-1}-1) \times (2^{n-1}-1)+2\times2\times (2^{n-1}-1)]$$

进行化简即为

$$sum_x=x\times[1+2\times (2^{n-1}-1)\times (2^{n-1}+1)]=x\times [1+2\times(2^{2(n-i)}-1)]$$

接下来考虑如何将其转化到层上去，我们发现，其实每层的节点他们的子树都是一模一样的，所不同的只是系数，我们设 $sum_i$ 表示第 $i$ 层所有节点编号值的和，则有：

$$ans=\sum_{i=1}^{i<=n}sum_i\times [1+2\times(2^{2(n-i)}-1)]$$

设 $numl_i$ 表示第 $i$ 层最左边节点的编号， $numr_i$ 表示第 $i$ 层最右边节点的编号，则有：

$$numl_i=2^{i-1} , numr_i=numl_i+2^{i-1}-1$$

$$sum_i=\frac {(numl_i+numr_i)\times 2^{i-1}}{2}=\frac{3\times 2^{2(i-1)}-2^{i-1}}{2}$$

则

$$ans=\sum_{i=1}^{i<=n} \frac{3\times 2^{2(i-1)}-2^{i-1}}{2}+(3\times 2^{2(i-1)}-2^{i-1})(2^{2(n-1)}-1)=\sum_{i=1}^{i<=n}(3\times 2^{2(i-1)}-2^{i-1})(2^{2(n-1)}-\frac{1}{2})$$

展开即为

$$ans=\sum_{i=1}^{i<=n}3\times2^{2(n-1)}-2^{2n-i-1}+\frac{1}{2}\times 2^{i-1}-\frac{3}{2}\times 2^{2(i-1)}$$

然后再展开

$$ans=3n\times2^{2(n-1)}+\frac{1}{2}\times \sum_{i=1}^{i<=n}2^{i-1}-\frac{3}{2}\times \sum_{i=1}^{i<=n}2^{2(i-1)}-2^{2n}\sum_{i=1}^{i<=n}\frac{1}{2^{i+1}}$$

然后，又有

$$\sum_{i=1}^{i<=n}2^{i-1}=2^n-1$$

后面的两个求和式用到等比数列求和的知识，即

$$\sum_{i=1}^{i<=n}2^{2(i-1)}=\frac{1-2^{2n}}{1-2^2}=\frac{2^{2n}-1}{3}$$

$$\sum_{i=1}^{i<=n}\frac{1}{2^{i+1}}=\frac{\frac{1}{4}\times(1-(\frac{1}{2})^n)}{1-\frac{1}{2}}$$

最后得到的答案为：

$$ans=3n\times 2^{2n-2}+2^n-2^{2n}$$

然后就做完了。

更新：此题根本不用快速幂，可以通过直接 $O(n)$ 的预处理避免超时，下面是最新代码。

CODE

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e6+10,MOD=998244353;
inline ll read()
{
    ll s=0,w=1;
    char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-') w=-1;ch=getchar();}
    while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
    return s*w;
}
ll dis[N];
int main()
{
	ll t=read();
	dis[0]=1;
	for(register int i=1;i<=1e6;i++) dis[i]=dis[i-1]*2%MOD;
	while(t--){
		ll n=read(),temp=dis[n-1];
		ll ans=((3*n%MOD-4+MOD)%MOD*temp%MOD*temp%MOD+temp*2%MOD+MOD)%MOD;
		printf("%lld\n",ans);
	}
	return 0;
}