JZOJ6680. 【2020.06.02省选模拟】路

Description

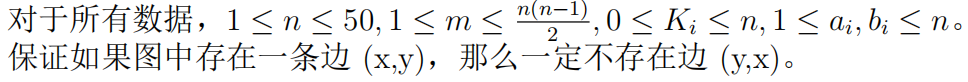
source:CF331E1,E2

Solution

• 比赛的时候想到了正解主要的部分，但是由于一些性质没有想清楚，所以导致没有打出来。
• 首先手玩一下可以发现任意一个合法的路径一定存在某一条边(x,y)上的序列有相邻的x,y，由于有多对x,y，我一开始的做法就是枚举从哪一对x,y向两边拓展，不难发现拓展是线性的，只需要到2*n（注意点数是 2 *n+1）就好。
• 只需要上面的方法就可以获得40%。
• 上面的路径一定是极短的。有了上面的思路就不难想到找出所有极短的路径，把它们拼在一起。要么边的序列包括所有端点（称开头和结尾为端点），要么不包括一个端点，要么不包括两个端点，但是后面两种情况用上面的东西去拓展显然存在拓展不出来的情况。至此我考场上就卡住了QAQ。
• 通过之后的思考我得出了以下的性质：
  1.如果边的序列不包括起点，那么起点后第一条边(st,x)的序列第一个一定是x。否则这条边就没有必要存在。（不包括终点同理）
  2.边的数量大于1，并且序列不包括两个端点，这样的路径不存在。否则中间一定可以断开。
• 那么对于不包括一个的就从一端往另一端扩展即可。
• 再加上空的边即可DP。
• 预处理：$O(n^3)$。DP：$O(n^4)$

#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#define maxn 105
#define ll long long 
#define mo 1000000007
using namespace std;


int n,m,i,j,k,x,y,tp;
int a[maxn][maxn][maxn],b[maxn][maxn],tk[maxn][maxn];
int A[maxn],B[maxn],C[maxn];
ll f[maxn][maxn][maxn][4],g[maxn][maxn][2],ans[maxn];

void Find(int X,int Y){
	int i,j,k=0;
	for(int t=1;t<tk[X][Y];t++) if (a[X][Y][t]==X&&a[X][Y][t+1]==Y) k++;
	if (k==1) for(int t=1;t<tk[X][Y];t++) if (a[X][Y][t]==X&&a[X][Y][t+1]==Y){
		A[0]=0; for(i=t;i>=1;i--) A[++A[0]]=a[X][Y][i];
		int bz=1;
		for(i=1;i<A[0];i++){
			x=A[i+1],y=A[i]; if (!b[x][y]) {bz=0;break;}
			for(j=tk[x][y];j>=1;j--){
				A[++A[0]]=a[x][y][j];
				if (A[0]>2*n+1) {bz=0;break;}
			} if (!bz) break;
		}
		if (!bz) continue;
		B[0]=0; for(i=t+1;i<=tk[X][Y];i++) B[++B[0]]=a[X][Y][i];
		for(i=1;i<B[0];i++){
			x=B[i],y=B[i+1]; if (!b[x][y]) {bz=0;break;}
			for(j=1;j<=tk[x][y];j++) {
				B[++B[0]]=a[x][y][j];
				if (B[0]>2*n+1) {bz=0;break;}
			} if (!bz) break;
		}
		if (!bz||A[0]+B[0]>2*n+1) continue;
		if (!tp) {
			tp=1,printf("%d\n",A[0]+B[0]);
			for(i=A[0];i>=1;i--) printf("%d ",A[i]);
			for(i=1;i<=B[0];i++) printf("%d ",B[i]);
			printf("\n");
		}
		f[A[A[0]]][B[B[0]]][A[0]+B[0]-1][0]++;
		g[A[0]+B[0]-1][B[B[0]]][1]++;
	}
	if (!tk[X][Y]) f[X][Y][1][3]++; else {
		if (a[X][Y][tk[X][Y]]==X){
			A[0]=0; for(i=tk[X][Y];i>=1;i--) A[++A[0]]=a[X][Y][i];
			int bz=1;
			for(i=1;i<A[0];i++){
				x=A[i+1],y=A[i]; if (!b[x][y]) {bz=0;break;}
				for(j=tk[x][y];j>=1;j--){
					A[++A[0]]=a[x][y][j];
					if (A[0]>2*n) {bz=0;break;}
				} if (!bz) break;
			}
			if (bz) 
				f[A[A[0]]][Y][A[0]][1]++,g[A[0]][Y][0]++;
		}
		if (a[X][Y][1]==Y){
			A[0]=0; for(i=1;i<=tk[X][Y];i++) A[++A[0]]=a[X][Y][i];
			int bz=1;
			for(i=1;i<A[0];i++){
				x=A[i],y=A[i+1]; if (!b[x][y]) {bz=0;break;}
				for(j=1;j<=tk[x][y];j++){
					A[++A[0]]=a[x][y][j];
					if (A[0]>2*n){bz=0;break;}
				} if (!bz) break;
			}
			if (bz) f[X][A[A[0]]][A[0]][2]++;
		}
	}
}

int main(){
//	freopen("path.in","r",stdin);
//	freopen("path.out","w",stdout);
	scanf("%d%d",&n,&m);
	for(i=1;i<=m;i++){
		scanf("%d%d",&x,&y),b[x][y]=1;
		scanf("%d",&tk[x][y]);
		for(j=1;j<=tk[x][y];j++) scanf("%d",&a[x][y][j]);
	}
	for(i=1;i<=n;i++) for(j=1;j<=n;j++) if (b[i][j]) 
		Find(i,j);
	if (!tp) printf("0\n\n");
	for(i=1;i<=2*n;i++) for(x=1;x<=n;x++) for(j=0;j<2;j++) if (g[i][x][j]){
		for(k=1;i+k<=2*n;k++) for(y=1;y<=n;y++){
			if (!j&&f[x][y][k][0]) 
				(g[i+k][y][1]+=g[i][x][j]*f[x][y][k][0])%=mo;
			if (!j&&f[x][y][k][1]) 
				(g[i+k][y][0]+=g[i][x][j]*f[x][y][k][1])%=mo;
			if (j&&f[x][y][k][2])  
				(g[i+k][y][1]+=g[i][x][j]*f[x][y][k][2])%=mo;
			if (j&&f[x][y][k][3])  
				(g[i+k][y][0]+=g[i][x][j]*f[x][y][k][3])%=mo;
		}
		if (j) ans[i]+=g[i][x][j];
	}
	for(i=1;i<=2*n;i++) printf("%lld\n",ans[i]%mo);
}