JZOJ6693. 【2020.06.05省选模拟】紫色彼岸樱推迟绽放
Description
幽幽子饿了,妖梦需要给幽幽子准备食物。
有 T 天,每天幽幽子划分成了 k 个时段,妖梦需要安排每一天的日程。
第 i 天妖梦准备了 D+i-1 道菜,每道菜有无数个。第 1 个时段是早餐,幽幽子会选择 L 道不同的菜吃。
接下来 k-1 个时段,每个时段可以选择 D+i-1 道菜中的一道吃或者选择 A 个活动中的一个参加,但是出于健康考虑,幽幽子不能连续两个时段同时吃菜。
k 和 A 是幽幽子事先决定好的,她给出了 Q 个询问,每次询问给出 L,D,T,问这 T 天每一天的安排的方案数之和。
由于答案可能很大,输出答案对 998244353 取模之后的结果。
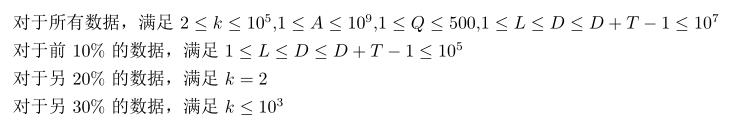
Solution
- 因为太菜了以及懒得打公式就直接从题解上搬了,这种神奇的推式子姿势和套路我是第一次见,生成函数以及奇怪的式子我还是做的少了。
![在这里插入图片描述]()
- 然后就有很骚的一步,用上升幂尝试去把阶乘消掉
![在这里插入图片描述]()
- 原式的阶乘拆开,将它代回去就可以消.
![在这里插入图片描述]()
- 然后“套路”地化简,将后面配一个阶乘
![在这里插入图片描述]()
- 后面是一列组合数的和。
- 现在考虑求,与读入的东西无关,只要能求出来就能完成一次询问。
- 然后又是一个很骚的套路,将的点值代进去,解出
- 把写成组合数,然后再配一个负数组合数上去:
![在这里插入图片描述]()
- 二项式反演就可以得到了,直接卷积
![在这里插入图片描述]()
- 最后再用组合意义矩阵乘法DP求出的-1…-k点值就好了。
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#define maxm 10100005
#define maxn 500005
#define ll long long
#define mo 998244353
using namespace std;
int n,A,Q,i,j,k,bt[maxn],lim;
ll fct[maxm],invf[maxm],a[maxn],b[maxn],c[maxn];
ll C(int n,int m){
if (n<m) return 0;
return fct[n]*invf[m]%mo*invf[n-m]%mo;
}
ll ksm(ll x,ll y){
ll s=1;
for(;y;y/=2,x=x*x%mo) if (y&1)
s=s*x%mo;
return s;
}
ll G[2],H[2][2],g[2],h[2][2];
ll F(ll x){
G[0]=1,G[1]=A;
H[0][0]=0,H[0][1]=x*A%mo;
H[1][0]=1,H[1][1]=A;
for(int t=n-2;t;t/=2){
if (t&1){
memset(g,0,sizeof(g));
for(int i=0;i<2;i++) for(int j=0;j<2;j++)
(g[j]+=G[i]*H[i][j])%=mo;
memcpy(G,g,sizeof(G));
}
memset(h,0,sizeof(h));
for(int i=0;i<2;i++) for(int j=0;j<2;j++) for(int k=0;k<2;k++)
(h[i][k]+=H[i][j]*H[j][k])%=mo;
memcpy(H,h,sizeof(H));
}
return G[1];
}
void dft(ll *a,int sig){
for(int i=0;i<lim;i++) if (i<bt[i]) swap(a[i],a[bt[i]]);
for(int mid=1;mid<lim;mid<<=1){
ll gn=ksm(3,(mo-1)/(mid<<1));
if (sig<0) gn=ksm(gn,mo-2);
for(int j=0;j<lim;j+=(mid<<1)%mo){
ll g=1;
for(int k=0;k<mid;k++,g=g*gn%mo){
ll x=a[j+k],y=a[j+k+mid]*g;
a[j+k]=(x+y)%mo,a[j+k+mid]=(x-y)%mo;
}
}
}
}
int main(){
// freopen("bloom.in","r",stdin);
// freopen("bloom.out","w",stdout);
scanf("%d%d%d",&n,&A,&Q);
fct[0]=1;for(i=1;i<maxm;i++) fct[i]=fct[i-1]*i%mo;
invf[maxm-1]=ksm(fct[maxm-1],mo-2);
for(i=maxm-2;i>=0;i--) invf[i]=invf[i+1]*(i+1)%mo;
for(i=0;i<n;i++) a[i]=F(-i-1)*invf[i]%mo*((i&1)?-1:1);
for(i=0;i<n;i++) b[i]=invf[i];
for(lim=1;lim<=2*n;lim<<=1);
for(i=1;i<lim;i++) bt[i]=(bt[i>>1]>>1)|((i&1)?lim>>1:0);
dft(a,1),dft(b,1);
for(i=0;i<lim;i++) c[i]=a[i]*b[i]%mo;
dft(c,-1);
ll inv=ksm(lim,mo-2);
for(i=0;i<lim;i++) c[i]=c[i]*inv%mo;
while (Q--){
ll L,D,T,ans=0;
scanf("%lld%lld%lld",&L,&D,&T),D--;
for(i=0;i<n;i++)
ans+=fct[i+L]*c[i]%mo*(C(i+D+T+1,i+L+1)-C(i+D+1,i+L+1))%mo;
ans=(ans%mo*invf[L]%mo+mo)%mo;
printf("%lld\n",ans);
}
}



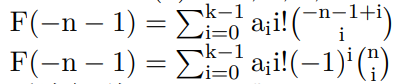

 浙公网安备 33010602011771号
浙公网安备 33010602011771号