二水中分白鹭洲
二水中分白鹭洲
题目大意
假设水中 \(n\) 条体积相等的鱼将按顺序依次排列，准备进行战斗。初始时，每条鱼可以选择向左游或向右游；但是鱼儿不太聪明，它们只会随机选择初始方向。
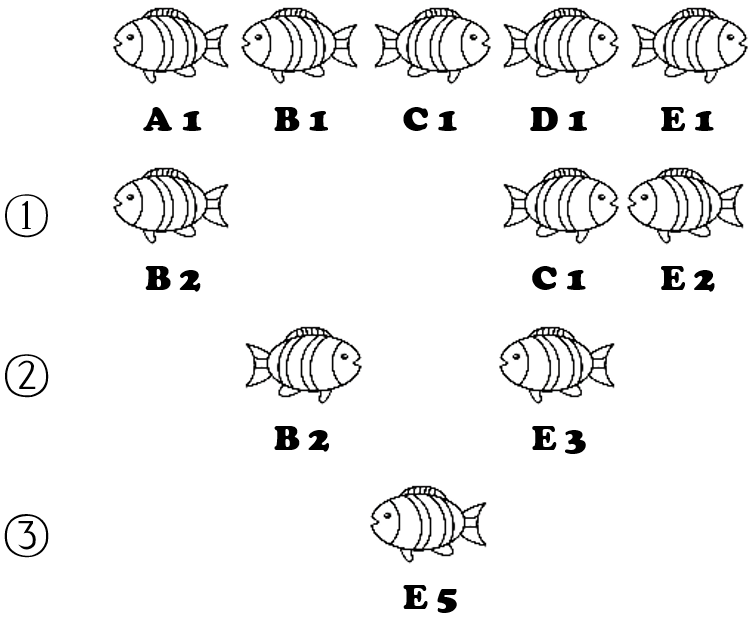
战斗时，若两条不同方向的鱼相遇，则体积大的鱼会吃掉体积小的鱼；如果两条鱼的体积相同，则向左游的鱼会吃掉向右游的鱼。吃完后，剩下的那条鱼按照自己原本的方向继续前行，同时体积变为原两鱼体积之和。可以认为吃鱼的过程在瞬间完成。
无论体积的大小，鱼儿们的速度始终保持一致。这样战斗可能永远不会结束，因此李白又划定了战斗的边界：如果鱼儿到达边界，则它必须立刻掉头。当然，掉头的过程也在瞬间完成。这样直到只剩一条鱼时，战斗结束。
解题思路
很有意思的一道题目。
性质
首先我们要发现一个性质。由于题目只说了顺次排列，并不是等距排列，所以尽管鱼以相同的速度移动，但时间发生的先后顺序可能有所不同。
同样的，这启发我们，无论按照何种操作顺序，最后的赢家总是相同的。
更严谨的，我们可以做以下思考。
鱼相对位置的改变必然伴随着吃与被吃事件的发生，故鱼永远是顺序的。
由于鱼的速度相同，所以相同方向的鱼不可以互相吃，换而言之，只有相邻且方向相反的鱼才能发生吃与被吃的事件。
不存在因为操作顺序不同而导致一条鱼吃大了再把另一条没吃够的鱼吃掉的情况。因为鱼永远是顺序的，而一条鱼只能吃掉同方向的鱼，所以在另一条鱼没吃够之前，两条鱼是不互相接触的。
暴力
答案求 \(2^n * \sum i * p_i\)。
由于总共只有 \(2^n\) 中情况，记 \(i\) 赢的次数为 \(c_i\)。
答案即求 \(\sum i * c_i\)。
我们先考虑暴力，枚举每一条鱼游的方向，关键在于如何求出最后剩下哪一条鱼。
上文论述了操作顺序是无序的，我们梳理一下，一共有三种操作。
- 最左边的调头
- 最右边的调头
- 吃与被吃事件
我们先让左右两边的调头，显然的是，接下来的方向序列中必有两条鱼相邻且反向。
故我们可以找到第一条向左游的鱼。接着它会把它左边的鱼全部吃掉，然后调头向右。
接着我们又可以找到第一条向左的鱼（否则，由于最后一条必定向左，所以如果没有向左的鱼了，那么最后也只剩一条鱼了）。
它会将从第二条开始的鱼全部吃掉。如果上一条鱼的坐标为 \(i\)，这一条鱼的坐标为 \(j\)，那么这一条鱼体积为 \(j-i\)。又上一条鱼的体积为 \(i\)。
- 如果 \(j-i \geq i\) 即 \(j \geq 2*i\) 那么这一条鱼把上一条鱼吃掉。
- 否则，上一条鱼把这一条鱼吃掉。
最后的体积都为 \(j\)。
一直重复上述过程，得到最后赢家即为：
最后一条 向左游并满足 \(j \geq 2*i\) 的鱼。
\(i,j\) 定义同上，其中 最后一条 的要求是为了保证它不被后面的鱼吃掉。
核心代码：
int lst=0,ans=0;
p[1]=1,p[n]=0;
for(int i=1;i<=n;i++){
if(p[i]==0){
if(i-lst>=lst) ans=i;
lst=i;
}
}
优化
考虑动态规划，设 \(f(i)\) 表示满足 \(i \geq 2*j\) 即 \(j \leq \lfloor \frac{i}{2} \rfloor\)（其中 \(j\) 为上一条向左游的鱼）的方案数。
容易得到转移方程：
其中：
- \((j,i)\) 中全部向右，\([1,j)\) 随意，所以权值 \(2^{j-1}\)。
- 第一条不可能向左，所以从 \(2\) 开始
- 加二是因为 \(i\) 可以作为第一条向左的鱼，并且第一条初始时可以向左或向右，因为会先调头向右，再开始操作。
推导一下，把外面的一提进去，运用等比数列求和公式：
注意到这里求出的 \(f(i)\) 只满足了一个条件，另一个条件 最后一条 并没有被满足。
故设 \(g(i)\) 表示只有 \(i\) 条鱼时的答案。
其中若要从 \(g(j)\) 转移过来（中间全部向右），需要保证 \(2*j > i\) 即 \(j > \lfloor \frac{i}{2} \rfloor\)，使得 \(i\) 不满足第一个条件，否则前面的答案就失效了（因为 \(i\) 一定满足第二个条件）。
此时 \(i\) 必定满足条件二，所以，记得加上自己的贡献。
故有状态转移方程：
可以使用前缀优化做到 \(O(n)\)，二的幂可以直接递推处理。
代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int maxn=1e7;
int n,mod;
int f[maxn+5],g[maxn+5];
int sm[maxn+5],pw[maxn+5];
int ans;
signed main(){
scanf("%lld%lld",&n,&mod);
pw[0]=1,pw[1]=2;
for(int i=1;i<=n;i++){
pw[i]=pw[i-1]*2%mod;
f[i]=pw[i/2];
g[i]=(sm[i-1]-sm[i/2]+f[i]*i)%mod;
sm[i]=(sm[i-1]+g[i])%mod;
}
ans=2*g[n]%mod;
printf("%lld",(ans+mod)%mod);
return 0;
}
