虚树

虚树

简介

虚树一般用于 树形DP 中，可以有效减少冗余的计算量。

其原理是将对 DP 无影响，或者在影响可快速运算范围内的点缩在一起，从而使得整棵树大小极大的减小。

因此，可以使用虚树的题目一般有 特殊点 之类的设定，多测并限定 特殊点 的总量。

P2495 [SDOI2011] 消耗战

一道经典的虚树题。

如果要考虑虚树，我们需要先考虑原树上是如何 DP 的。

DP

设 \(f(u)\) 表示切断 \(u\) 子树中所有能源所需要的代价。

记 \(v\) 表示 \(u\) 的儿子，\(w\) 为 \(u\) 到其父亲的边权。

若 \(u\) 有能源：

\[f(u) = w \]

直接切断 \(u\) 到父亲的桥梁。

若 \(u\) 无能源：

\[f(u) = \min\{w,\sum f(v)\} \]

虚树

点

接下来考虑有哪些点可以省去。

观察状态转移方程，能源点肯定需要保留，能源点两两之间的 LCA 也需要保留。

当然，作为 DP 的起点，根节点也需要被保留。

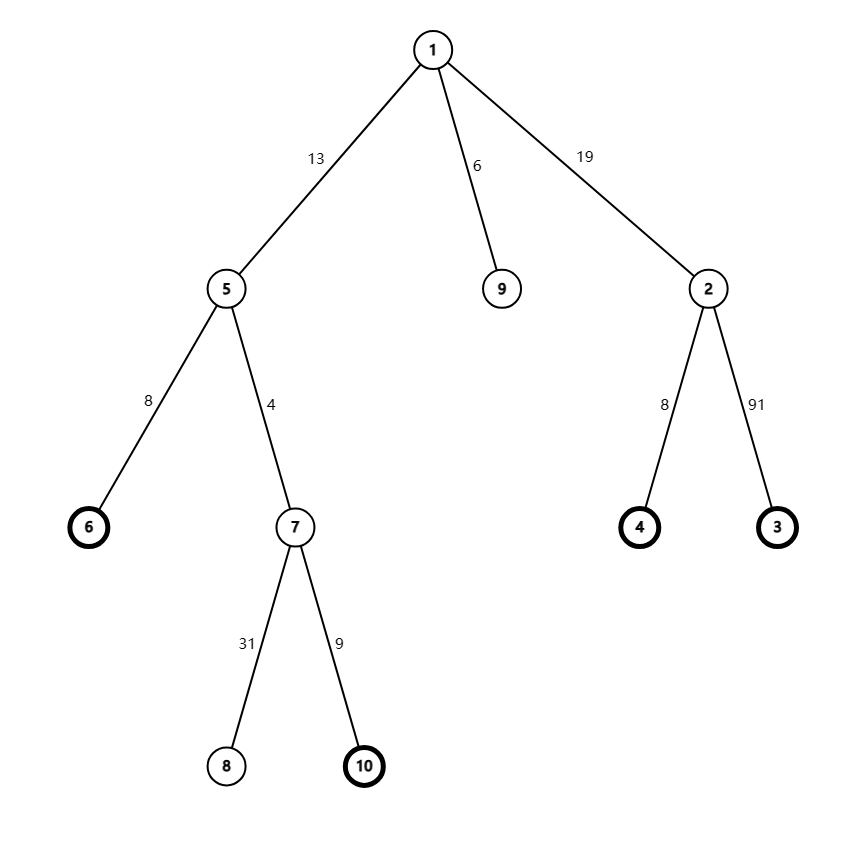
即如图若加粗的点为能源点，则 5，2，1，都需要保留。

边

接着考虑边，根据此题状态转移方程，虚树上的边权应该为连接的两点原树上之间的最小边权。

建树

关键在于如何高效的建树，即确定需要保留的点之间的父子关系。

一种方法是将关键点按照 DFS序 排序，将相邻的关键点的 LCA 求出。

再将关键点的 LCA 与 关键点按照 DFS序 排序与去重。

证明：

由于按照 DFS序 排序，一个显然的性质是两个点的 LCA 比他们中间任意两个点的 LCA 都不靠后。并且对于不相邻的两个点，他们的 LCA 一定是上述 LCA 中的一个，因为总存在一个点其到 \(u\) 或 \(v\) 的 LCA 为 \(lca(u,v)\)，这是容易用反证法的到的。

将相邻关键点的 LCA 向这两个关键点中 DFS序 较大的连边。

证明：

如果 \(u\) 是 \(v\) 的祖先，\(u\) 到 \(v\) 路径上没有关键点，成立

否则，可以证明 \(lca(u,v)\) 到 \(v\) 也没有关键点，成立。

代码链接

总结

时间复杂度 \(O(n \log n)\)。

此建树方法常数较大。