最大全1子矩阵的两种解法（例题：City Game HDU - 1505）
以前牛客多校遇到过两道，都没做出来，这次来系统性的补习一下。
例题：City Game HDU - 1505
题意：给你一个矩阵，求最大全1子矩阵，最后结果乘以3。。。
全1矩阵可以参考下图
这个框就代表一个全1矩阵，且图中所示是一个极大全1矩阵（四条边都有0）
当然他也是一个最大全1矩阵。
做法一：单调栈+预处理
我们先把 01矩阵预处理，对于第 j 列，从第一行从头开始扫描至最后一行，得到第一个 “1” 向下的最大拓展长度（遇到“0”）；
如果把上图预处理，就能得到：
0 1 1 0 1 1 1
0 2 2 1 2 2 0
1 3 3 2 3 3 0
2 4 4 0 0 4 1
当前点是1，上面的点权值>0 ，那么长度拓展；如果遇到0，不再拓展，直到遇到新的1，便又开始拓展。
这是扫描所有的列的结果，当然，也可以扫描行。
然后就用单调栈求解每一行更新最大值，相当于在每一行建立一个笛卡尔树（笛卡尔树其实也是基于单调栈建立的）。
例如第4行，
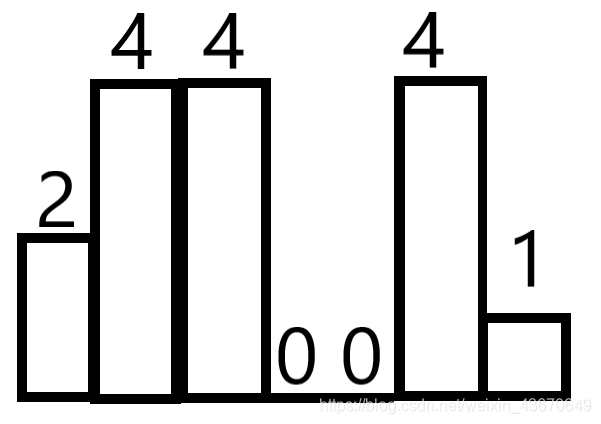
维护一个单调不下降的栈，大于等于栈顶入栈，并且储存位置（在哪一列），小于则出栈，通过之前储存的序列位置 pos、和所能影响的最左位置 l、和当前出栈的位置，从左向右处理，求得矩形的宽度，高度就是他本身的值 v；上图栈的运行如下：
（入栈前算最左位置 l，就等于栈顶的pos+1；pos 可以通过循环次数看出 , v 就是预处理后的每个点的值； 也可以不算 l , 在元素出栈后直接调用栈顶的pos+1 也行 )
a[1]=2 入栈 ，a[2]=4>=2 入栈，a[3]=4>=4 入栈，a[4]=0 < a[3]出栈 ans=max(ans,（出栈位置-最左位置）*a[3] ) , 0 < a[2]出栈同理……
AC代码
#include<cctype>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<stack>
using namespace std;
typedef long long LL;
const int N=1e3+5;
const int inf=0x3f3f3f3f;
#define fi first
#define se second
int read()
{
int x=0,t=1;
char ch=getchar();
while(!isdigit(ch)){ if(ch=='-')t=-1; ch=getchar(); }
while(isdigit(ch)){ x=10*x+ch-'0'; ch=getchar(); }
return x*t;
}
struct node
{
int l,v,pos;
node(){}
node(int ll,int vv,int pp)
{
l=ll; v=vv; pos=pp;
}
};
int a[N][N];
char s[2];
stack<node> sta;
int main()
{
int T=read();
while(T--)
{
int n=read(),m=read();
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
scanf("%s",s);
if(s[0]=='F') a[i][j]=1;
else a[i][j]=0;
}
}
for(int i=1;i<=m;i++)
{
for(int j=1;j<=n;j++)
{
if(a[j][i]&&a[j-1][i])
a[j][i]+=a[j-1][i];
}
}
int ans=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
while(!sta.empty()&&sta.top().v>a[i][j])
{
ans=max(ans,sta.top().v*(j-sta.top().l) );
sta.pop();
}
sta.push(node(sta.empty()?1:sta.top().pos+1,a[i][j],j) );
}
while(!sta.empty() )
{
ans=max(ans,sta.top().v*(m+1-sta.top().l) );
sta.pop();
}
}
printf("%d\n",ans*3);
}
}
滚动数组 做法模板：
#include<bits/stdc++.h>
using namespace std;
const int N = 1e3+5;
int a[N][N];
int h[N],l[N],r[N];
int n,ans;
void init()
{
ans=0;
memset(l,0,sizeof(l) );
memset(r,0,sizeof(r) );
memset(h,0,sizeof(h) );
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
init();
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
char s[2];
scanf("%s",s);
if(s[0]=='F') a[i][j]=1;
else a[i][j]=0;
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
if(!a[i][j]) h[j]=0;
else h[j]++;
for(int j=1;j<=m;j++)
{
l[j]=j;
while(l[j]>1&&h[j]<=h[l[j]-1]) l[j]=l[l[j]-1];
}
for(int j=m;j>=1;j--)
{
r[j]=j;
while(r[j]<n&&h[j]<=h[r[j]+1]) r[j]=r[r[j]+1];
}
for(int j=1;j<=m;j++)
ans=max(h[j]*(r[j]-l[j]+1),ans);
}
printf("%d\n",ans*3);
}
return 0;
}
做法二：悬线法(待更新)
。。。
#include<bits/stdc++.h>
using namespace std;
const int N = 1e3+5;
int a[N][N],h[N],l[N],r[N];
void init(int m)
{
memset(h,0,sizeof(h));
for(int i=1;i<=m;i++) l[i]=1,r[i]=m;
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
int n,m,ans=0;
scanf("%d%d",&n,&m);
init(m);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
char s[2];
scanf("%s",s);
if(s[0]=='F') a[i][j]=1;
else a[i][j]=0;
}
for(int i=1;i<=n;i++)
{
int ll=1,rr=m;
for(int j=1;j<=m;j++)
{
if(!a[i][j]) ll=j+1,l[j]=1,h[j]=0;
else ++h[j],l[j]=max(ll,l[j]);
}
for(int j=m;j>=1;j--)
{
if(!a[i][j]) rr=j-1,r[j]=m;
else r[j]=min(rr,r[j]);
ans=max(ans,(r[j]-l[j]+1)*h[j]);
}
//for(int j=1;j<=m;j++)printf("%d%c",r[j],j==m?'\n':' ');
}
printf("%d\n",ans*3);
}
return 0;
}
最大全1正方形（待更新）
。。。
