Typora数学公式

LaTeX编辑数学公式基本语法元素

LaTeX中的数学模式有两种形式:

• inline 和 display。

  • 前者是指在正文插入行间数学公式,后者独立排列,可以有或没有编号。

• 行间公式(inline)

  • 用$将公式括起来。

• 块间公式(displayed)

  • 用$$将公式括起来是无编号的形式
  • 还有[.....]的无编号独立公式形式但Markdown好像不支持。
  • 块间元素默认是居中显示的。

各类希腊字母编辑表

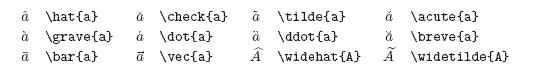
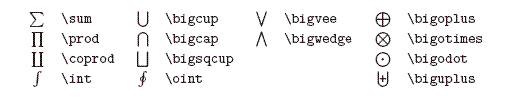
• 上下标、根号、省略号

  • 下标：x_i:\(x_i\)
  • 上标：x^2: \(x^2\)
  • 注意：上下标如果多于一个字母或者符号，需要用一对{}括起来 x_{i1}: \(x_{i1}\) \(x^{at}\)
  • 根号: \sqrt[n]{5}: \(\sqrt[n]{5}\)
  • 省略号：\cdots: \(\cdots\)

• 运算符

  • 基本运算符+ - * ÷

    • 求和:

      • \sum_1^n: \(\sum_1^n\)
      • \sum_{x,y}: \(\sum_{x,y}\)

    • 积分:

      • \int_1^n: \(\int_1^n\)

    • 极限

      • lim_{x \to \infy}: \(lim\_{x \to \infty}\)

    • 行列式

      • $$
        X=\left|
        	\begin{matrix}
        		x_{11} & x_{12} & \cdots & x_{1d}\\
        		x_{21} & x_{22} & \cdots & x_{2d}\\
        		\vdots & \vdots & \ddots & \vdots \\
        		x_{11} & x_{12} & \cdots & x_{1d}\\
        	\end{matrix}
        \right|
        $$
        

        \[X=\left| \begin{matrix} x_{11} & x_{12} & \cdots & x_{1d}\\ x_{21} & x_{22} & \cdots & x_{2d}\\ \vdots & \vdots & \ddots & \vdots \\ x_{11} & x_{12} & \cdots & x_{1d}\\ \end{matrix} \right| \]

    • 矩阵

      • $$
        	\begin{matrix} 
        	1 & x & x^2\\ 
        	1 & y & y^2\\ 
        	1 & z & z^2\\ 
        	\end{matrix}
        $$
        

        \[\begin{matrix} 1 & x & x^2\\ 1 & y & y^2\\ 1 & z & z^2\\ \end{matrix} \]

• 箭头

  • 

• 分段函数

  • $$
    f(n)=
    	\begin{cases}
    		n/2, & \text{if $n$ is even}\\
    		3n+1,& \text{if $n$ is odd}
    	\end{cases}
    $$
    

    \[f(n)= \begin{cases} n/2, & \text{if $n$ is even}\\ 3n+1,& \text{if $n$ is odd} \end{cases} \]

• 方程组

  • $$
    \left\{
    	\begin{array}{c}
    		a_1x+b_1y+c_1z=d_1\\
    		a_2x+b_2y+c_2z=d_2\\
    		a_3x+b_3y+c_3z=d_3
    	\end{array}
    \right.
    $$
    

    \[\left\{ \begin{array}{c} a_1x+b_1y+c_1z=d_1\\ a_2x+b_2y+c_2z=d_2\\ a_3x+b_3y+c_3z=d_3 \end{array} \right. \]

• 常用公式

  • 线性模型

    • $$
      	h(\theta) = \sum_{j=0} ^n \theta_j x_j
      $$
      

      \[h(\theta) = \sum_{j=0} ^n \theta_j x_j \]

  • 均方误差

    • $$
      	J(\theta) = \frac{1}{2m}\sum_{i=0}^m(y^i - h_\theta(x^i))^2
      $$
      

      \[J(\theta) = \frac{1}{2m}\sum_{i=0}^m(y^i - h_\theta(x^i))^2 \]

  • 求积公式

    • \$$
      	H_c=\sum_{l_1+\dots +l_p}\prod^p_{i=1} \binom{n_i}{l_i}
      \$$
      

      $$ H_c=\sum_{l_1+\dots +l_p}\prod^p_{i=1} \binom{n_i}{l_i} $$

  • 批量梯度下降

    • $$
      	\frac{\partial J(\theta)}{\partial\theta_j} = -\frac1m\sum_{i=0}^m(y^i - 	h_\theta(x^i))x^i_j
      $$
      

      \[\frac{\partial J(\theta)}{\partial\theta_j} = -\frac1m\sum_{i=0}^m(y^i - h_\theta(x^i))x^i_j \]

  • 推导过程

    • $$
      \begin{align}
      	\frac{\partial J(\theta)}{\partial\theta_j}
      	& = -\frac1m\sum_{i=0}^m(y^i - h_\theta(x^i)) \frac{\partial}{\partial\theta_j}(y^i-h_\theta(x^i))\\
      	& = -\frac1m\sum_{i=0}^m(y^i-h_\theta(x^i)) \frac{\partial}{\partial\theta_j}(\sum_{j=0}^n\theta_j x^i_j-y^i)\\
      	&=-\frac1m\sum_{i=0}^m(y^i -h_\theta(x^i)) x^i_j
      \end{align}
      $$
      

      \[\begin{align} \frac{\partial J(\theta)}{\partial\theta_j} & = -\frac1m\sum_{i=0}^m(y^i - h_\theta(x^i)) \frac{\partial}{\partial\theta_j}(y^i-h_\theta(x^i))\\ & = -\frac1m\sum_{i=0}^m(y^i-h_\theta(x^i)) \frac{\partial}{\partial\theta_j}(\sum_{j=0}^n\theta_j x^i_j-y^i)\\ &=-\frac1m\sum_{i=0}^m(y^i -h_\theta(x^i)) x^i_j \end{align} \]

• 字符下标

  • $$
    \max \limits_{a<x<b}\{f(x)\}	
    $$
    

    \[\max \limits_{a<x<b}\{f(x)\} \]

• end