2018 CCPC Girl Contest
Time：2018.6.3
Link 中文题面
A
题意
给一个长度为n的序列，有m个询问，每个询问三个数 l，r，d，问a[l] ×a[l+1]×.....×a[r]，是否为d的倍数 （n<=1e5，1<=l<=r<=n，a[i]<=1e5 ，d<=1e5 ）
分析
直接的想法是，对每个数分解质因数，维护一个前缀质因数和，对于每次询问，查询区间[l,r]的质因数是否全部含有d的质因数即可，具体写起来需要先筛出1e5内的素数，然后前缀维护，由于1e5内的素数大概有1000个， T*1e8，时间复杂度和空间复杂度都差一点
那么我们思考如何优化：考虑对每一个a[i]分解质因数的时候，将当前位置放到一个数组里，对每次询问对d的质因数直接二分[l,r]看是否大于d的数量即可
时间复杂度O(T*nlogn)
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn = 1e5+7;
vector<int>G[maxn];
int t,n,q,l,r,d;
int a[maxn];
void init()
{
for(int i=1;i<=100000;i++)
G[i].clear();
}
void oula(int x,int id)
{
for(int i=2;i*i<=x;i++)
{
if(x&&x%i==0)
{
while(x%i==0)
{
x/=i;
G[i].push_back(id);
}
}
}
if(x>1)
G[x].push_back(id);
}
int main()
{
scanf("%d",&t);
while(t--)
{
scanf("%d%d",&n,&q);
init();
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
oula(a[i],i);
}
while(q--)
{
scanf("%d%d%d", &l, &r, &d);
bool flag=true;
for(int i=2;i*i<=d;i++)
{
if(d&&d%i==0)
{
int cnt=0;
while(d%i==0)
{
++cnt;
d/=i;
}
int num=upper_bound(G[i].begin(),G[i].end(),r)-lower_bound(G[i].begin(),G[i].end(),l);
if(cnt>num)
flag=false;
}
}
if(d>1)
{
int num=upper_bound(G[d].begin(),G[d].end(),r)-lower_bound(G[d].begin(),G[d].end(),l);
if(num==0)
flag=false;
}
if(flag)
printf("Yes\n");
else
printf("No\n");
}
}
return 0;
}
B
题意
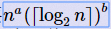<=k，给出a，b，k，问最大的n为多少，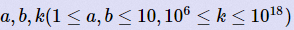
分析
注意到a，b最大只有10，二分n，无脑直接乘的话会爆long long，想起乘法运算，可以先除判断是否可以乘A×B>C的话，可以转化为A>C/B
#include<bits/stdc++.h>
#define ll long long
using namespace std;
long long k;
int a,b;
bool co(long long n)
{
long long g=ceil(log2(n));
long long now=1;
for(int i=1;i<=b;i++)
{
if(k/g<now)return 0;
else now*=g;
}
for(int i=1;i<=a;i++)
{
if(k/n<now)return 0;
else now*=n;
}
return 1;
}
int main()
{
int T;
scanf("%d",&T);
for(int i=1;i<=T;i++)
{
scanf("%d %d %lld",&a,&b,&k);
long long ss=2,tt=1e18+10,mid;
while(ss!=tt)
{
mid=(ss+tt)/2;
if(co(mid+1))
ss=mid+1;
else tt=mid;
}
printf("%lld\n",ss);
}
}
C
分析
贪心会死的很惨，因为假如有一个点很大，其中g>k个点较大，且最大的更优，但走不了这g个点，贪心gg
正解：dp
定义：dp[i][j][x][y]：在点（i，j），考虑了前 i-1行 和 第 i 行前 j 个，有x个经过的没算进去，y个没经过的算进去了 的最大值
转移：右移 ：到点（i，j+1），直接可以由dp[i][j][x][y]的所有状态转移过来
下移 ：到点（i+1，j+1），需要将第 i 行的 j+1 ~ m 和第 i+1 行的 1~j-1 单独取出来考虑
答案：dp[n][m][t][t] (0<=t<=k)
时间复杂度：O(n^2×k^3)trick：转移细节有点难写
#include <cstdio>
#include <cstring>
#include <algorithm>
#include<bits/stdc++.h>
using namespace std;
int Case;
int n,m,k,a[52][52],dp[52][52][22][22];
int s[52];
bool cmp(int x,int y)
{
return x>y;
}
int main()
{
scanf("%d", &Case);
while(Case--)
{
scanf("%d%d%d", &n, &m, &k);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
scanf("%d", &a[i][j]);
}
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
for(int x=0;x<=k;x++)
for(int y=0;y<=k;y++)
dp[i][j][x][y]=-1;
dp[1][1][0][0]=a[1][1];
dp[1][1][0][1]=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
int cnt=1;
for(int p=1;p<=m;p++)
{
if(p==j)
continue;
if(p<j) s[cnt++]=a[i+1][p];
else s[cnt++]=a[i][p];
}
sort(s+1,s+cnt,cmp);
for(int x=2;x<cnt;x++)
s[x]+=s[x-1];
for(int x=0;x<=k;x++)
{
for(int y=0;y<=k;y++)
{
if(~dp[i][j][x][y])
{
if(j<m)
{
dp[i][j+1][x][y]=max(dp[i][j][x][y]+a[i][j+1], dp[i][j+1][x][y]);
dp[i][j+1][x][y]=max(dp[i][j+1][x][y], dp[i][j][x-1][y]);
if(y<k)
dp[i][j+1][x][y+1]=max(dp[i][j+1][x][y+1],dp[i][j][x][y]);
}
if(i<n)
{
for(int g=0;g<=m-1;g++)
{
if(g+x>k)
break;
dp[i+1][j][x+g][y]=max(dp[i+1][j][x+g][y], dp[i][j][x][y]+a[i+1][j]+s[g]);
if(y<k)
dp[i+1][j][x+g][1+y]=max(dp[i+1][j][x+g][y+1],dp[i][j][x][y]+s[g]);
}
}}
}
}
}
}
int ans=0;
for(int i=0;i<=k;i++)
ans=max(ans,dp[n][m][i][i]);
printf("%d\n",ans);
}
return 0;
}
D
分析
注意到，1到n的总cost ， log(1+a[1])/(1) + log(1+a[1]+a[2])/(1+a[1]) + ......+ log(1+.....+a[n])/(1+......a[n-1]) = log(1+sum[n])，直接dijskar的时候加上限制即可
时间复杂度O(mlogn)
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn = 1e5+7;
int head[maxn*2],nxt[maxn*2],to[maxn*2],tot,w[maxn*2],lim[maxn*2];
ll d[maxn];
int t,n,m,u,v,a,b;
bool vis[maxn];
void init()
{
tot=0;
memset(head,0,sizeof(head));
memset(nxt,0,sizeof(nxt));
}
struct node{
int v;
ll w;
friend bool operator < (node a,node b){
return a.w > b.w;
}
};
void addedge(int u,int v,int a,int b)
{
++tot;
w[tot]=a;
lim[tot]=b;
to[tot]=v;
nxt[tot]=head[u];
head[u]=tot;
}
int dij()
{
for(int i=1;i<=n;i++)
d[i]=1e14+5;
memset(vis,false,sizeof(vis));
d[1]=1;
priority_queue<node>q;
q.push({1,1});
while(!q.empty())
{
node k=q.top();
q.pop();
int v=k.v;
ll ww=k.w;
if(vis[v]) continue;
vis[v]=1;
for(int i=head[v];i;i=nxt[i])
{
int t=to[i];
double cost=log2((1.0*(ww+w[i]))/(ww));
if(d[t]>ww+w[i] && cost>=lim[i])
{
d[t]=ww+w[i];
q.push({t,d[t]});
}
}
}
if(d[n]== 1e14+5) return -1;
double ans=log2(d[n]+1LL);
return int(ans);
}
int main()
{
scanf("%d",&t);
while(t--)
{
init();
scanf("%d%d", &n, &m);
for(int i=1;i<=m;i++){
scanf("%d%d%d%d", &u, &v, &a,&b);
addedge(u,v,a,b);
}
int ans=dij();
if(ans!=-1)
printf("%d\n",ans);
else
printf("%d\n",ans);
}
return 0;
}
E
题意
分析
F
分析
经典的树上莫队 / 二分+主席树的问题
重点在于每次询问怎么正确找出符合条件的最小值，考虑将1~2e6分块，每块sqrt(2e6)，在树上操作的时候修改每个点权出现的次数，最后直接check每块出现奇数次的数字是否等于区间长度即可
时间复杂度O( m×sqrt(n) )常数有点大
分块真的优秀啊
undate：1. ym的sb树分块的写法被卡成sb了啊，以后还是用栈写吧！！！
2. ym对分块后的询问sort也一无所知啊，应该拿belong[ L ] (左端点所在的块) 为first key ，dfn[x] (每个点访问的时间戳) 为second key
#include<algorithm>
#include<iostream>
#include<stdio.h>
#include<string.h>
#include<map>
#include<set>
using namespace std;
const int maxn = 200000+7;
int head[maxn],nxt[maxn*2],to[maxn*2],tot;
int t,n,m,u,v,col[maxn];
int fa[maxn][30],d[maxn],dfn[maxn];
int belong[maxn],block,num,cnt,s[maxn],f[maxn],Ans[maxn],ans[maxn],bl[maxn+10000];
bool vis[maxn],vv[maxn];
struct node
{
int l,r,id;
friend bool operator < (node a,node b)
{
if(belong[a.l] != belong[b.l])
return belong[a.l] < belong[b.l];
else
return belong[a.r] < belong[b.r];
}
}q[maxn];
int kk;
void init()
{
cnt=tot=kk=num=0;
memset(Ans,0,sizeof(Ans));
memset(nxt,0,sizeof(nxt));
memset(f,0,sizeof(f));
memset(vis,false,sizeof(vis));
memset(head,0,sizeof(head));
memset(d,0,sizeof(d));
memset(dfn,0,sizeof(dfn));
}
void addedge(int u,int v)
{
to[++tot]=v;
nxt[tot]=head[u];
head[u]=tot;
}
void dfs(int x)
{
vis[x]=1;
dfn[x]=++kk;
int bottom=cnt;
for(int i=head[x];i;i=nxt[i])
{
int v=to[i];
if(!vis[v])
{
d[v]=d[x]+1;
fa[v][0]=x;
dfs(v);
if(cnt - bottom >= block)
{
++num;
while(cnt!=bottom){
belong[s[cnt--]]=num;
}
}
}
}
s[++cnt]=x;
}
void init_rmq()
{
fa[1][0]=1;
for(int j=1;j<=25;j++)
for(int i=1;i<=n;i++)
fa[i][j]=fa[fa[i][j-1]][j-1];
}
int LCA(int u,int v)
{
if(d[u]<d[v])
swap(u,v);
int dc=d[u]-d[v];
for(int i=0;i<25;i++){ //调至同一高度
if((1<<i)&dc)
u=fa[u][i];
}
if(u==v) return u; // 一个点恰好是另一个点的lca
for(int i=24;i>=0;i--){ //找到可以跳的最大的步数，使得(u,v)的lca不同
if(fa[u][i] != fa[v][i])
{
u=fa[u][i];
v=fa[v][i];
}
}
return fa[u][0]; //u，v最后一定在lca的下面
}
void rev(int x)
{
if(!vis[x]){
f[col[x]]++;
if(f[col[x]]%2)
Ans[bl[col[x]]]++;
else
Ans[bl[col[x]]]--;
vis[x]=1;
}
else{
f[col[x]]--;
if(f[col[x]]%2)
Ans[bl[col[x]]]++;
else
Ans[bl[col[x]]]--;
vis[x]=0;
}
//vis[x]^=1;
}
void solve(int uu,int vv)
{
while(uu!=vv)
{
if(d[uu] > d[vv])
swap(uu,vv);
rev(vv);
vv=fa[vv][0];
}
}
int main()
{
int k=(sqrt(205000));
for(int i=1;i<=205000;i++)
bl[i]=(i-1)/k+1;
scanf("%d", &t);
while(t--)
{
scanf("%d%d", &n, &m);
block=sqrt(n);
init();
for(int i=1;i<=n;i++)
scanf("%d", &col[i]);
for(int i=1;i<=n-1;i++)
{
scanf("%d%d", &u, &v);
addedge(u,v);
addedge(v,u);
}
dfs(1);
init_rmq();
++num;
while(cnt)
belong[s[cnt--]]=num;
for(int i=1;i<=m;i++)
{
scanf("%d%d", &u, &v);
if(belong[u] > belong[v])
swap(u,v);
q[i].l=u;
q[i].r=v;
q[i].id=i;
}
sort(q+1,q+m+1);
q[0].l=q[0].r=1;
for(int i=1;i<=m;i++)
{
int lca=LCA(q[i].l,q[i].r);
solve(q[i-1].l, q[i].l);
solve(q[i-1].r, q[i].r);
rev(lca);
int op;
for(int i=1;i<=k+1;i++)
{
if(Ans[i] != k)
{
for(int j=(i-1)*k+1;j<maxn;j++)
{
if(f[j]%2==0)
{
op=j;
break;
}
}
break;
}
}
ans[q[i].id]=op;
rev(lca);
}
for(int i=1;i<=m;i++)
{
printf("%d\n",ans[i]);
}
// init();
}
return 0;
}
G
分析
签到
H
题意
给出长度为n的一个字符串，判断以第一个元素为结尾的字符串与以第二个元素为结尾的字符串大小，第二和第三，到第n-1到n
分析
类似KMP的思想，查询第一个时顺便算出后面的答案
O(N)的复杂度
期间用cin读取1e6的字符串超时了，下次注意用scanf
I
题意
分析
J
题意
分析
K
简单的模拟题，视力好就行
Summary
Ym：电子竞技不需要视力，K题没仔细看题wa了一发，ym A题没想出来有点过分啊，还好czh写出b题
Czh:
dijsktar可以转化，其实不难，可以做，高估了这题
iterator lower_bound( const key_type &key ): 返回一个迭代器，指向键值>= key的第一个元素。
iterator upper_bound( const key_type &key ):返回一个迭代器，指向键值<=key的最后一个元素的后一个元素。
