导数入门
Part1 什么是导数
百度百科释义：导数，也叫导函数值。又名微商，是微积分中的重要基础概念。当函数 \(y=f(x)\) 的自变量 \(x\) 在一点 \(x_0\) 上产生一个增量 \(Δx\) 时，函数输出值的增量 \(Δy\) 与自变量增量 \(Δx\) 的比值在 \(Δx\) 趋于 0 时的极限 \(a\) 如果存在，\(a\) 即为在 \(x0\) 处的导数，记作 \(f'(x)\)。
Part2 导数有什么作用
导数是用来反映函数局部单调性的工具。 一个函数在某一点的导数描述了这个函数在这一点附近的变化率。通俗来讲，导数描述了该函数在这点附近的波动趋势。所以，在高中数学里面我们一般利用导数来进行对函数极值的求解。
Part3 普通函数求导
基本公式是这样的：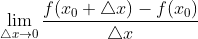
但是我们初中生肯定是不懂的对叭，所以这里有一些导数基本公式：
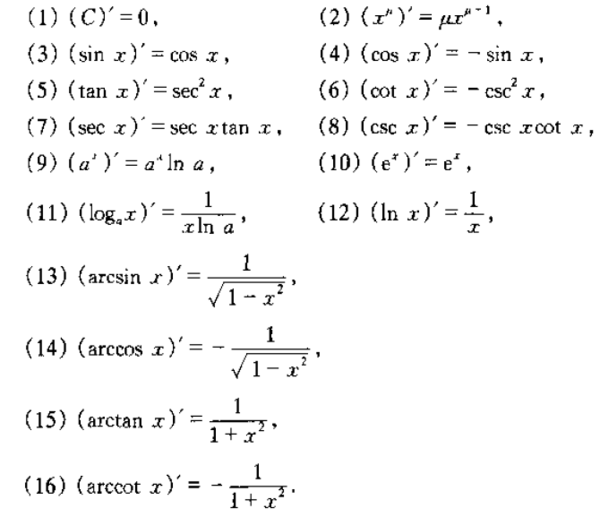
同时有一些运算法则：
（ \(C\) 是常数）
比如我们要求二次函数 \(y=f(x)=ax^2+bx+c\) 的最值，因为这个二次函数图像只有一个波峰/波谷，其最值就是极值。
所以我们根据以上公式对原函数进行求导：
令 \(f_1(x)=ax^2\) , \(f_2(x)=bx\) , \(f_3(x)=c\) ，根据导数的加法法则，有：\(f'(x)=f_1'(x)+f_2'(x)+f_3'(x)\)。
我们分别对三个函数进行求导： \(f_1'(x)=2ax, f_2'(x)=b,f_3'(x)=0\)。
所以:\(f'(x)=2ax+b\)。当导数值等于 0 时，原函数取得极值，所以一个二次函数取得极值就是在 \(x=-\displaystyle{\frac{b}{2a}}\)的位置。
Part4 复合函数求导
对于复合函数 \(y=f(g(x))\) ，若 \(u=g(x)\) ，则 \(y_x'=y_u'\times u_x'\)。
比方说 \(y=\ln \sin x\) ，对它求导，可这么做：
令 \(y=f(u)=\ln u\),\(u=g(x)=\sin x\)，那么 \(y_x'=y_u'\times u_x'=\displaystyle{\frac{1}{u}}\times \cos x=\displaystyle{\frac{\cos x}{\sin x}}=\cot x\)。
Part5 例题
- \(y=x^5+\displaystyle{\frac{1}{x}}\)+114514，求 \(y'\)
- \(y=\log_{a}{x}+e^x\)-54188，求 \(y'\)
- \(y=\log_{a}{\sin {\frac{637}{7x^2}}}\)，求 \(y'\)
