阿氏圆拓展
\(\quad\) 我们知道，阿氏圆在初中数学中是一类常用的求线段和/差极值的模型，它的大致题意如下：
平面上有一个圆 \(O\) , 圆外两点 \(A\) 和 \(B\) ，圆上有一动点 \(P\) 。现在给出一个值 \(k=\frac{r}{OA}\) ，求 \(kPA+PB\) 的最小值与 \(kPA-PB\) 的最大值。
\(\quad\) 但是，你以为我今天要讨论的是这两种人尽皆知的问题吗？既然 \(P\) 是 \(⊙O\) 上的一个动点，那么 \(kPA+PB\) 一定会有最大值， \(kPA-PB\) 也会有最小值。
\(\quad\) 坦白来讲，对于一个初三学生来说，找到这两个 \(P\) 的位置绝非易事，于是我在经历了 4 天的思考后，向 \(\text{TEoS}\) 神仙求助了 \((kPA+PB)_{max}\) 的情况，随后自己整理出了 \((kPA-PB)_{min}\) 的情况。
- \((kPA+PB)_{max}\)
话不多说，先放原图：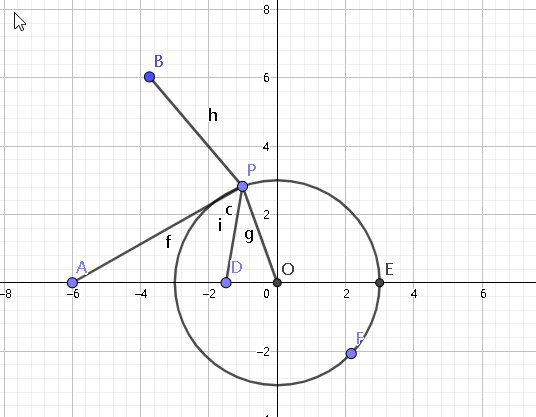
\(D\) 我们构造的点，满足 \(kPA=PD\) 。于是问题转化为求 \((BP+PD)_{max}\) 。
乍一看，这运用初中的知识完全求不出来，但是我们可以稍稍试试转化法：如果能找到满足 \((BP+PD)_{max}\) 时点 \(P_0\) 的轨迹，再与圆 \(O\) 的交点，这不就是最终的 \(P\) 了吗？
随后，我们引入高中的内容：椭圆。椭圆，即平面上到两焦点的距离之和为定值的点的集合，而这个定值就是椭圆的长轴的长度。既然如此，我们就可以以 \(B\) , \(D\) 两点为焦点，构造椭圆，当椭圆与 \(⊙O\) 相切时，\(BP+PD\) 取得 \(max\) 值。
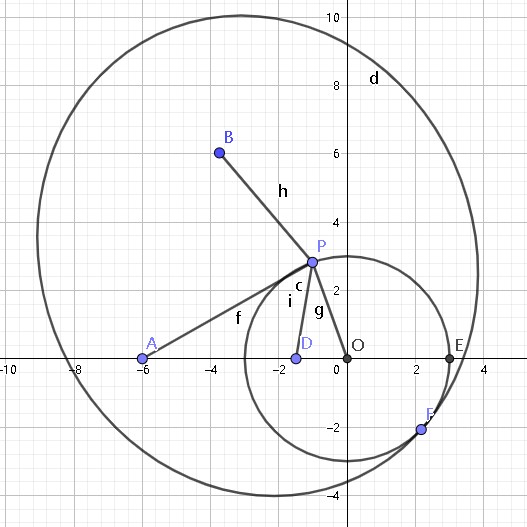
如图可见，点 \(F\) 就是椭圆和 \(⊙O\) 的切点，当 \(P\) 与 \(F\) 重合时，由于“椭圆的长轴最长”，所以此时 \(BP+PD\) 取得 \(max\) 。可是，怎样求具体的值呢？\(\text{TEoS}\) 神仙 给出了一种方案：
也就是说，我们可以求出切线方程，由于 \(P(F)\) 此时是切点，所以椭圆的切线就是圆的切线，随后带入元和数值求解即可。理论上可行，实际应该有点麻烦（因为要对高次方程进行求解）。
- \((kPA-PB)_{min}\)
还是同样的思路，首先构造点 \(D\) ，然后找出 \(PD-PB\) 的轨迹，最后与 \(⊙O\) 的切点即为点 \(P\)。
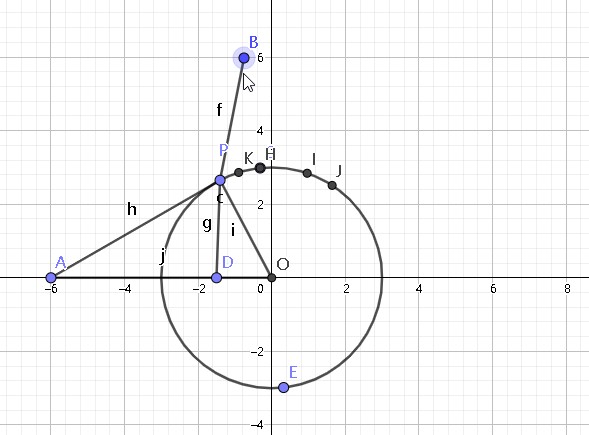
于是我们再次引入高中的内容：双曲线。双曲线就是平面上到两焦点的距离之差相等的点的集合。于是，我们以 \(B,D\) 为焦点，构造双曲线。当双曲线与 \(⊙O\) 相切时，切点即为点 \(P\) 。
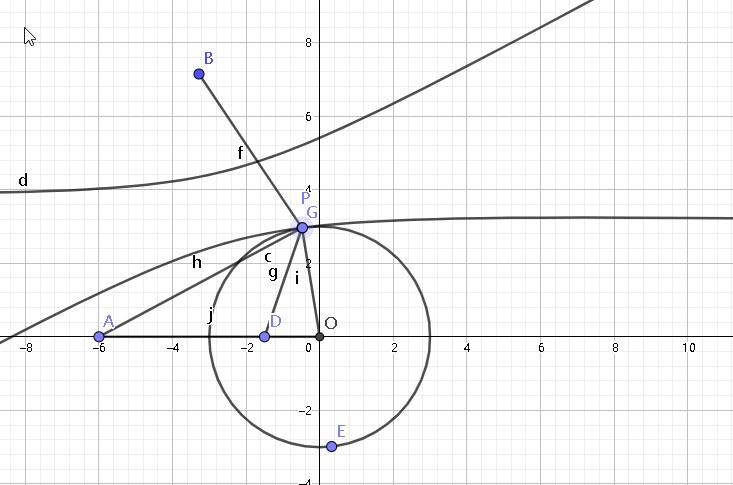
这个是下曲线与 \(⊙O\) 相切的情况，还有一种上曲线和 \(⊙O\) 相切的情况：
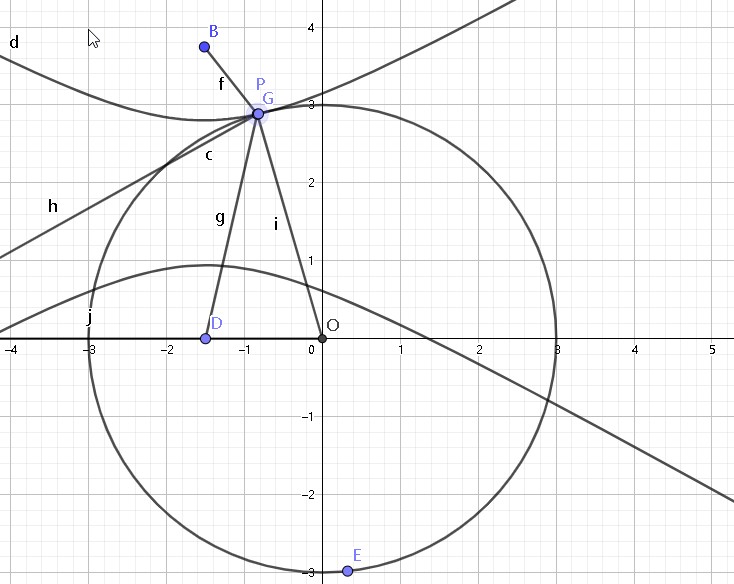
那么计算的话就自行按照双曲线和圆的方程联立，思路还是和上面那种差不多。
