一本通1752题解

题意：

给定一个 $n\times m$ 的矩形，其中矩形左下角坐标为 $(1,1)$ ，右上角坐标为 $(n,m)$ 。现在矩形中有 $p$ 个小矩形，对于每个小矩形，我们用一个四元组 $(x1,y1,x2,y2)$ 描述它，其中 $(x1,y1)$ 是它的左下角坐标，$(x2,y2)$ 是它的右上角坐标。现在请你找到一个最大的，未被小矩形覆盖的正方形，并输出它的边长。

数据范围：

对于30%的数据，p≤1000。
对于70%的数据，p≤30000。
对于100%的数据，p≤4e5，m,n≤1e6。

算法分析：

第一个想法：$O(n^3)$ 暴力 $NB$！

但是 $O(n^3)$ 肯定是过不了这题的。通过数据范围，我们可以知道题目肯定是 $O(nlogn)$ 级别的。我们考虑优化 $O(n^3)$ 的算法使其变成 $O(nlogn)$ 级别。我们必须要从左向右枚举 $i,j$ ，这一维的 $O(n^2)$ 暂时是省不掉的，但是对于从下而上的这一维 $O(n)$ ，我们可以用线段树的扫描线进行维护，时间复杂度可以优化成 $O(logn)$ 级别，至此，我们已经将原算法优化到了 $O(n^2logn)$ (但还是过不了)。

接下来我们考虑继续优化。到这一步看似优无可优，实际玄机暗藏。我们不妨考虑贪心的思路，在 $n$ 这一维度上强制选择区间 $[l,r]$ 进行答案更新，随后对指针 $l$、$r$ 进行移动即可，时间复杂度 $O(nlogn)$（这也被称为双指针法）。

但是怎样具体实现呢？作者在这玄乎其玄的撤了半天，具体的思路一点也没告诉我们。~~不要急，马上来！~~首先看我的图：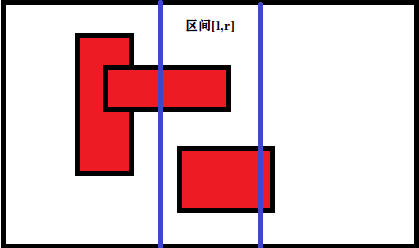

 

当前我们强制选取这两条蓝线之间的区间 $[l,r]$ 更新答案。假设当前我们扫描线扫除的结果为 $t[1].ans$，我们就可以直接用 $min(r-l+1,t[1].ans)$ 更新答案。很明显当前的 $t[1].ans$ 是大于 $r-l+1$ 的，对于这种情况，我们只需要不断右移 $r$ 指针即可。

那么什么时候我们要对 $l$ 指针进行操作呢，还是看图：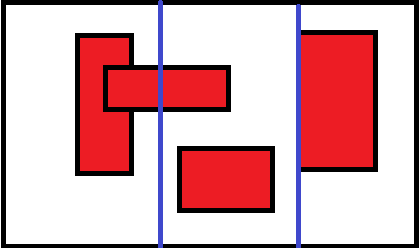

 

此时的 $r$ 指针已经向后移动了，我们的扫描线扫到的 $t[1].ans$ 此时小于 $r-l+1$,再让 $r$ 一直往后移动，我们就会错过很多答案（因为答案是取 $min(t[1].ans,r-l+1)$ )，所以我们此时让 $l$ 指针右移，当 $l$ 指针右移到某个位置时，会扫到矩形出边，以至于答案变得更优。

Code Share

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+100;
int n,m,p,ans=0;
struct Tree{
    int lx,rx,mx;
    int add;
}t[N<<2];
struct node{
    int h1,h2,state;
};
vector<node> pr[N];
inline int maxx(int x,int y){
    return x>y?x:y;
}
inline int mini(int x,int y){
    return x<y?x:y;
}
void build(int p,int l,int r){
    t[p].lx=t[p].rx=t[p].mx=r-l+1;
    t[p].add=0;
    if(l==r)return ;
    int mid=l+r>>1;
    build(p<<1,l,mid);
    build(p<<1|1,mid+1,r);
}
void pushup(int p,int l,int r,int mid){
    if(t[p].add){
        t[p].lx=t[p].rx=t[p].mx=0;
        return ;
    }
    if(l==r){
        t[p].lx=t[p].rx=t[p].mx=1;
        return ;
    }
    if(t[p<<1].mx^(mid-l+1)) //mid-l+1就是左边的长度
        t[p].lx=t[p<<1].lx; //直接用左儿子的左边更新他
    else
        t[p].lx=t[p<<1].mx+t[p<<1|1].lx; //否则是中间长度加右儿子的左边
    if(t[p<<1|1].mx^(r-mid))
        t[p].rx=t[p<<1|1].rx; //直接用右儿子的右边更新 
    else
        t[p].rx=t[p<<1|1].mx+t[p<<1].rx; //否则是中间长度加左儿子的右边
    t[p].mx=max(t[p<<1].rx+t[p<<1|1].lx,max(t[p<<1].mx,t[p<<1|1].mx));
}
void modify(int p,int l,int r,int ll,int rr,int op){
    if(l>=ll && r<=rr){
        t[p].add+=op;
        pushup(p,l,r,l+r>>1);
        return ;
    }int mid=l+r>>1;
    if(ll<=mid)
        modify(p<<1,l,mid,ll,rr,op);
    if(rr>mid)
        modify(p<<1|1,mid+1,r,ll,rr,op);
    pushup(p,l,r,mid);
}
int main(){
    scanf("%d %d %d",&n,&m,&p);
    build(1,1,m);
    for(int i=1;i<=p;i++){
        int a1,b1,a2,b2;
        scanf("%d %d %d %d",&a1,&b1,&a2,&b2);
        node xk,yk;
        xk.h1=b1,xk.h2=b2,xk.state=1;
        yk.h1=b1,yk.h2=b2,yk.state=-1;
        pr[a1].push_back(xk);
        pr[a2].push_back(yk);        
    }
    int l=1,r=1;
    for(;r<=n;++r)
    {
        for(int i=0;i<pr[r].size();i++) //从0到横坐标为r，开始扫一遍
            if(pr[r][i].state==1)  //入边
                modify(1,1,m,pr[r][i].h1,pr[r][i].h2,1);
        ans=maxx(ans,mini(r-l+1,t[1].mx)); //更新答案
        for(;t[1].mx<=r-l+1;++l) //贪心思路，右移指针L
            for(int i=0;i<pr[l].size();++i)
                if(pr[l][i].state==-1) //遇到出边 
                    modify(1,1,m,pr[l][i].h1,pr[l][i].h2,-1); //删除该矩形          
    }
    printf("%d",ans);
    return 0;
}