【模板】KMP

（比赛前最后的挣扎）

KMP是什么

高效的字符串匹配算法。可以用于查找字符串s中是否含有模式串p。

（剩下的简介自行百度）

思路与实现

万物先从暴力开始

怎样用暴力求出s串中是否含有p串？若含有请输出第一次出现的位置。

暴力就好

比对s[i]是否等于p[j]，若等则继续，若不等就让i回到i-j+1位置，j=0继续比对。

这个画个图就很好懂（因为它真的太暴力了）

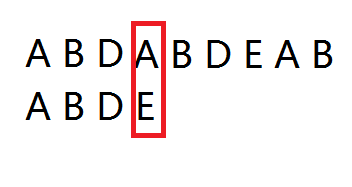
此时i=j=3 s[i]与p[j]不适配

所以i回到i-j+1 j=0

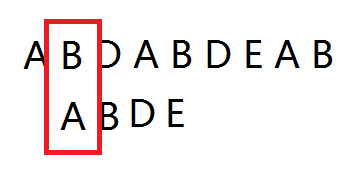
一直循环直至找到或者i=slen

这个过程一看就十分暴力，怎么优化呢？

观察下图：

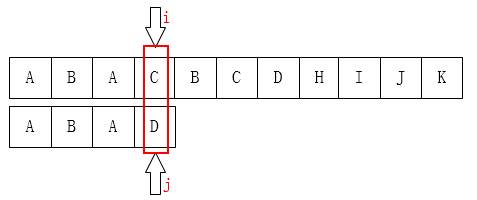
其实可以不用移动i，通过移动j来不断比对。

因为ABA中第0位A与第2位A相等，而此时对于S与P的前三个字符又是完全适配的。

所以可以像下图一样移动：

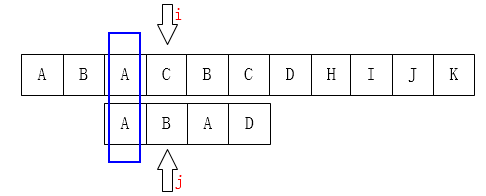
这样就可以节省不少时间。

所以得出大概思路：

先预处理出对于p中任意一个p[i],若不适配，应该向前移动到next[i]的位置，从而实现。

 而对于任意next[j]=k，j表示最大真后缀的结束位置，k表示最大真前缀的结束位置。

举个栗子：

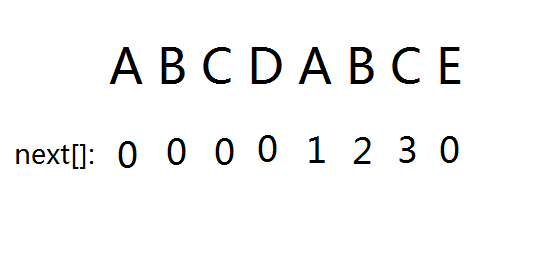
看懂了吗？

不需要知道为什么只需要知道这个东西是啥就行。

为什么一会就知道了hh

好的这究竟是为什么呢？

对于上述模式串：

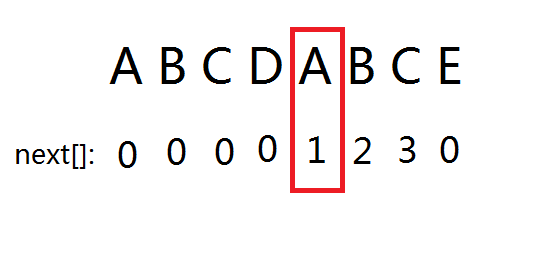
取第二个A分析，对于该模式串的一个子串

A B C D A

含有最长真前缀 A 和最长真后缀 A

所以对于位置 5 （也就是字符A）next[5]=最长真前缀的结束位置=1（也就是第一个字符A的位置）

所以只要处理出next数组，就可以得知当p[i]与s[j]失配时下一个应该i应该跳到什么地方。

这时屏幕前的你就会打出一个大大的问号：

这究竟是为什么？
再拟一组数据：

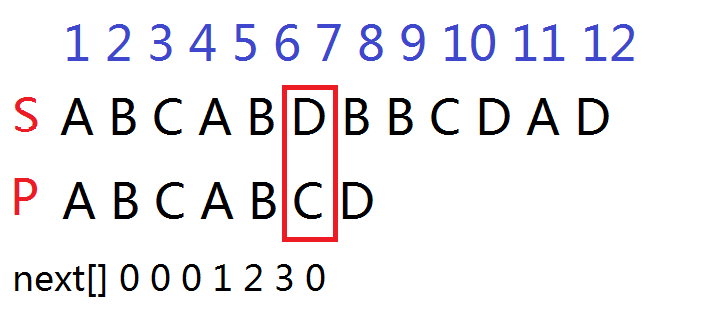
可以轻易看出：当第六位D C 不匹配时，会根据next[6]=3跳回第三位C

这样跳的原理是什么呢？

因为由上文中的暴力可知，若对于像上图这样前面所有的都适配且模式串中还有重复部分的情况，若用暴力会浪费很多时间。

因为已知在p[1]-p[5]完全适配，又因为p[1]-p[2]与p[4]-p[5]重合

所以肉眼可见，当模式串p整体右移一位时，s与p是不会适配的（不会的就自己手移叭）

而如果直接将j跳回第三位（第一个字符C）时，因为

 因为已知在p[1]-p[5]完全适配，又因为p[1]-p[2]与p[4]-p[5]重合

所以（还是看图吧）

 

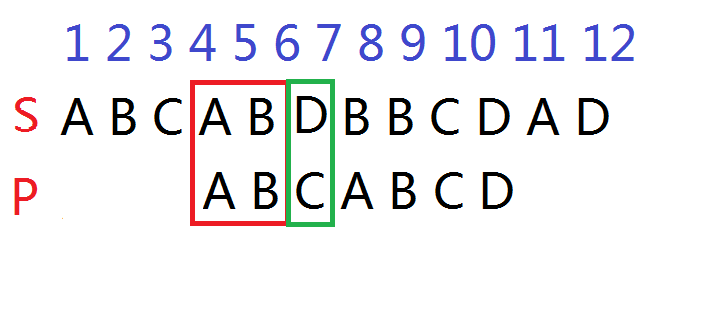
根据上图的next数组，j移到next[j]的位置，因为i不动，所以等价于将模式串p整体向右移，到p[next[j]]与s[i]对齐。

而因为s[1-2]=s[4-5]=p[1-2]=p[4-5]

所以得出p[1-2]与s[4-5]是一定适配的。

所以通过一次操作，将模式串p移动到了最优可能适配的位置。

为什么是最有可能适配呢？

原因看图：

由于暴力，所以当不适配时，i，j的移动等价于下图的移动（原串不变，模式串右移一位）

又因为用红框框出部分已经在前面的比对中知道他们是适配的了，而这里有存在重复的前缀后缀，所以这样移动是不会得到解的。

（看不懂上一行就手推一下叭）

而什么时候暴力会有可能得到解呢？

参考上上图，因为是循环是从前往后的，所以当前并不知道下一个字符是否适配，所以上上图是有可能得到一个解的。

而所以当前并不知道下一个字符是否适配这是为什么呢？

感性地思考下就会得出，因为在第一次比对中，会一直运行到第一个不匹配的位置，所以前面的所有字符都已知了，而对于暴力的每一次移动第一个字符都不会适配，所以会使模式串p不停地右移，直到达到如下效果：

 

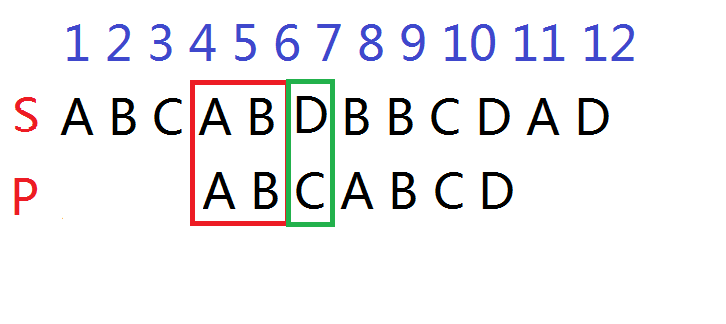
所以解释了为什么要这样移动模式串以及移动的原理。

然后问题就来了，怎样预处理出next数组呢？

（关于这玩意的写法老多了，选了一种最好理解的）

先看代码吧：

for(int i=2;i<=lenb;i++)
       {     
       while(j&&b[i]!=b[j+1])
        j=k[j];    
       if(b[j+1]==b[i])j++;    
        k[i]=j;
       }

首先，第五行的if应该很好懂，以上面的模式串p为例

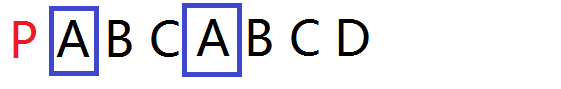
当这样相等时，j与i就同时后移，next[i]=j+1;

 那如果不相等要怎么办呢？

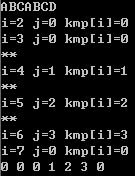
这里是分段输出，可以看出，当i指向模式串的最后一位D时，p[i]!=p[j]（此时j指向3）

这是就不能直接next[i]=j+1了，要去寻找一个更小的前缀，使该前缀的结束位置与当前i指向的字符相等。

再举一个栗子就是这样：

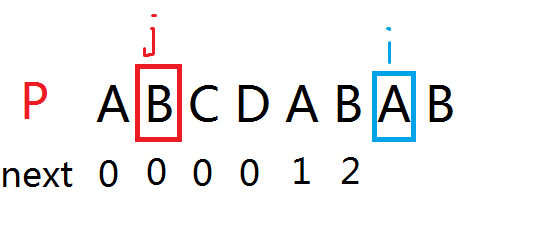
此时，p[j+1]!=p[i]，怎样寻找更小的前缀呢？

方案1：让j一个一个往前移动，直到找到一个字符与当前p[i]相等。

方案2：让j移动到p[next[j]]位置，再次比对，若不等则再次向前。

易得：方案一有一个漏洞。

因为一个一个向前移动，只能保证当前位置与p[i]相等，而无法比较之前位置，无法确定前缀是否完全相等。

那方案二是怎么实现的呢？

因为p[1-2]=p[4-5],所以所有的与p[1-2]相等的前缀一定都与p[4-5]相等，而比较的是当前所在的与p[1-2]相等后缀的后一位，如果相等，则找到了较小的相同前缀后缀

所以 k[i]=j+1

分段输出如下：

问题又来了，为什么要是while循环找较小呢？不可以用一个if替代吗？

万一一次找不到较小的呢？又因为对于next数组的一部分是有继承性的，所以这样就直接（wa）

但是这个代码还存在以下情况：

可以发现，这时的一次移动无效了。

原因是p[j]=p[next[j]]

因为这时已知的p[j]！=s[i],而p[j]=p[next[j]],所以p[next[j]]!=s[i]

所以这次转移是无效的。

怎么避免这样的无效转移呢？

（这里引用另一种写法（比较难理解））

void GetNextval(char* p, int next[])
{
    int pLen = strlen(p);
    next[0] = -1;
    int k = -1;
    int j = 0;
    while (j < pLen - 1)
    {
        //p[k]表示前缀，p[j]表示后缀  
        if (k == -1 || p[j] == p[k])
        {
            ++j;
            ++k;
            //较之前next数组求法，改动在下面4行
            if (p[j] != p[k])
                next[j] = k;   //之前只有这一行
            else
                //因为不能出现p[j] = p[ next[j ]]，所以当出现时需要继续递归，k = next[k] = next[next[k]]
                next[j] = next[k];
        }
        else
        {
            k = next[k];
        }
    }

}

但是这种写法与上一种写法的时间复杂度基本相同，但是这个不好理解，所以略过。

对于next数组的介绍就到这里，而对于next数组的用法已经在上文中有过。

（又到了激动人心的时刻）

代码实现：

#include<iostream>
#include<cstring>
using namespace std;
int nxt[1000001];
char s[1000001],p[1000001];
int main()
{
    cin>>s+1;
    cin>>p+1;
    int plen=strlen(p+1);
    int slen=strlen(s+1);
    int j=0;//模式串指针 
    for(int i=2;i<=plen;i++)
    {
        while(j&&p[i]!=p[j+1])
        j=nxt[j];
        if(p[i]==p[j+1])
        j++;
        nxt[i]=j; 
    }//预处理
    j=0;//不要忘记清零 
    for(int i=1;i<=slen;i++)
    {
        while(j&&s[i]!=p[j+1])
        j=nxt[j];
        if(s[i]==p[j+1])
            j++;
            if(j==plen)
            {
                cout<<i-j+1<<endl;
                j=nxt[j];//再寻找下一个位置 
            }
    } 
    for(int i=1;i<=plen;i++)
    {
        cout<<nxt[i]<<" ";
    }
    return 0;
}

 

模板指路：（CSP-S RP++!）

练习题指路：（power strings）（剪花布条）

再放一下有分段输出的代码

#include<iostream>
#include<cstring>
using namespace std;
int k[1000010];
int lena,lenb,j; 
char a[1000010],b[1000010];
int main()
{
    cin>>a+1;
    cin>>b+1;
    lena=strlen(a+1);
    lenb=strlen(b+1);
    for(int i=2;i<=lenb;i++)
       {     
       while(j&&b[i]!=b[j+1])
        cout<<"由"<<j<<"转移到"<<k[j]<<endl,j=k[j];    
       if(b[j+1]==b[i])cout<<"**"<<endl,j++;    
        k[i]=j;
        cout<<"i="<<i<<" "<<"j="<<j<<" "<<"kmp["<<i<<"]"<<"="<<k[i]<<endl; 
       }
    j=0;
    for(int i=1;i<=lena;i++)
       {
          while(j>0&&b[j+1]!=a[i])
           j=k[j];
          if(b[j+1]==a[i]) 
           j++;
          if(j==lenb) 
          {
                cout<<i-lenb+1<<endl;
                j=k[j];
          }
       }

    for(int i=1;i<=lenb;i++)
    cout<<k[i]<<" ";
    return 0;
}

 

CSP-S RP++!