P3205 [HNOI2010]合唱队
题面:
为了在即将到来的晚会上有更好的演出效果,作为AAA合唱队负责人的小A需要将合唱队的人根据他们的身高排出一个队形。假定合唱队一共N个人,第i个人的身高为Hi米(1000<=Hi<=2000),并已知任何两个人的身高都不同。假定最终排出的队形是A 个人站成一排,为了简化问题,小A想出了如下排队的方式:他让所有的人先按任意顺序站成一个初始队形,然后从左到右按以下原则依次将每个人插入最终棑排出的队形中:
-第一个人直接插入空的当前队形中。
-对从第二个人开始的每个人,如果他比前面那个人高(H较大),那么将他插入当前队形的最右边。如果他比前面那个人矮(H较小),那么将他插入当前队形的最左边。
当N个人全部插入当前队形后便获得最终排出的队形。
例如,有6个人站成一个初始队形,身高依次为1850、1900、1700、1650、1800和1750,
那么小A会按以下步骤获得最终排出的队形:
1850
-
1850 , 1900 因为 1900 > 1850
-
1700, 1850, 1900 因为 1700 < 1900
-
1650 . 1700, 1850, 1900 因为 1650 < 1700
-
1650 , 1700, 1850, 1900, 1800 因为 1800 > 1650
-
1750, 1650, 1700,1850, 1900, 1800 因为 1750 < 1800
因此,最终排出的队形是 1750,1650,1700,1850, 1900,1800
小A心中有一个理想队形,他想知道多少种初始队形可以获得理想的队形
大概思路:从最后的结果来看,队尾或队头一定是最后入队的,所以每次都分离队头和队尾,分别讨论他们的状态求解。(动规)
这个思路有点抽象。。举个例子解释一下 (以输入 1 2 3 5 4 作为例子)
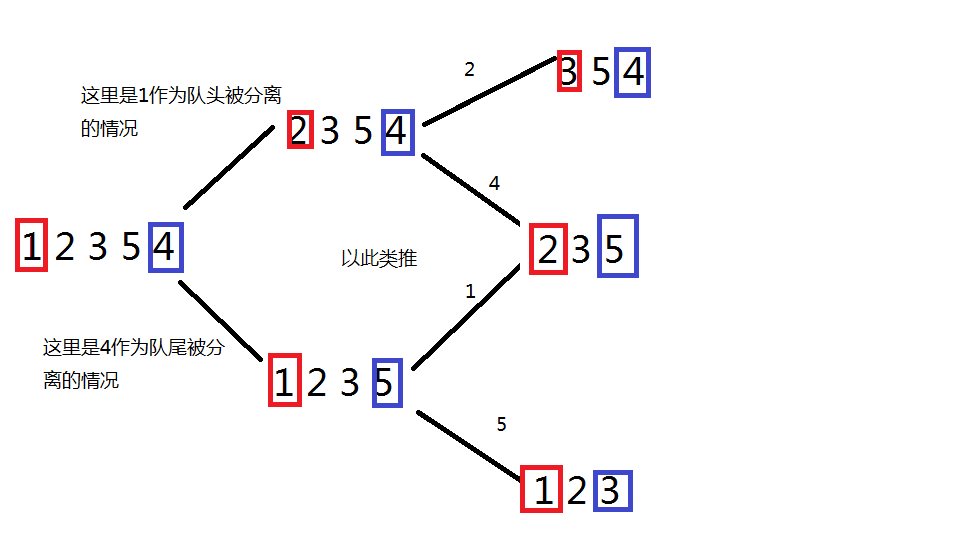
真的就是这么简单的分下去吗?
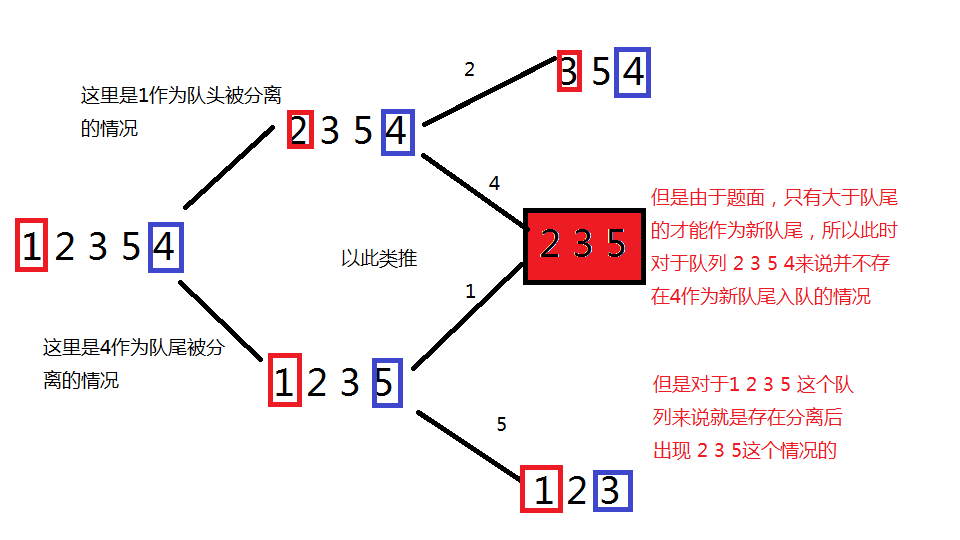
这个问题怎么解决呢?
这时,我们假设当前要讨论的数为x,删去x的队列队头值为L,队尾值为R。就能发现

x作为新队尾时也是同理(这里就不写了)
所以可以根据上图推出动态转移方程式
我们设队列为q[],方案数存储在dp[][][]中。
for(int len=n-1;len>=1;len--) { for(int l=1,r=len;r<=n;l++,r++) { dp[l][r][0]=((q[l]<q[r+1])*dp[l][r+1][1]+(q[l-1]<q[l])*dp[l-1][r][0])%Mod; dp[l][r][1]=((q[r]>q[l-1])*dp[l-1][r][0]+(q[r]<q[r+1])*dp[l][r+1][1])%Mod; } }
这里的0代表作为队头入队,1代表作为队尾入队。
最重要的部分到这里就结束啦!
下面是代码
#include<iostream> #include<cstdio> using namespace std; int dp[1010][1010][2]; int q[1010]; int Mod=19650827; int n; int main() { scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d",&q[i]); } q[0]=Mod; q[n+1]=-Mod; dp[1][n][0]=dp[1][n][1]=1; for(int len=n-1;len>=1;len--) { for(int l=1,r=len;r<=n;l++,r++) { dp[l][r][0]=((q[l]<q[r+1])*dp[l][r+1][1]+(q[l-1]<q[l])*dp[l-1][r][0])%Mod; dp[l][r][1]=((q[r]>q[l-1])*dp[l-1][r][0]+(q[r]<q[r+1])*dp[l][r+1][1])%Mod; } } int ans=0; for(int i=1;i<=n;i++) { ans=(ans+dp[i][i][0])%Mod;//这里直接输出dp[1][n][0]+dp[1][n][1]也行 } printf("%d",ans); return 0; }
蒟蒻的第一篇博客!(放个礼花吧先)


