Python3实现机器学习经典算法(一)KNN
一、KNN概述
K-(最)近邻算法KNN(k-Nearest Neighbor)是数据挖掘分类技术中最简单的方法之一。它具有精度高、对异常值不敏感的优点,适合用来处理离散的数值型数据,但是它具有 非常高的计算复杂度和空间复杂度,需要大量的计算(距离计算)。
它的工作原理是:如果已经给定一个带有标签(分类)的数据集(训练集),对于每一个给定的没有标签(分类)的新向量,通过计算该向量与训练集中的每一个向量的距离, 选择前k个最小的距离,在k个距离中出现次数最多的标签(分类)则是新向量的标签(分类)。
使用KNN算法将某个向量划分到某个分类中的过程如下:
1)计算训练集中的每个向量和当前向量之间的距离;
2)按照距离递增排序;
3)选择与当前向量距离最小的前k个向量;
4)计算前k个向量中每个类别的频率;
5)选择出现频率最高的类别作为新向量的分类。
二、准备数据集
Python3实现机器学习经典算法的数据集都采用了著名的机器学习仓库UCI(http://archive.ics.uci.edu/ml/datasets.html),其中分类系列算法采用的是Adult数据集(http://archive.ics.uci.edu/ml/datasets/Adult),测试数据所在网址:http://archive.ics.uci.edu/ml/machine-learning-databases/adult/adult.data,训练数据所在网址:http://archive.ics.uci.edu/ml/machine-learning-databases/adult/adult.test。
Adult数据集通过收集14个特征来判断一个人的收入是否超过50K,14个特征及其取值分别是:
age: continuous.
workclass: Private, Self-emp-not-inc, Self-emp-inc, Federal-gov, Local-gov, State-gov, Without-pay, Never-worked.
fnlwgt: continuous.
education: Bachelors, Some-college, 11th, HS-grad, Prof-school, Assoc-acdm, Assoc-voc, 9th, 7th-8th, 12th, Masters, 1st-4th, 10th, Doctorate, 5th-6th, Preschool.
education-num: continuous.
marital-status: Married-civ-spouse, Divorced, Never-married, Separated, Widowed, Married-spouse-absent, Married-AF-spouse.
occupation: Tech-support, Craft-repair, Other-service, Sales, Exec-managerial, Prof-specialty, Handlers-cleaners, Machine-op-inspct, Adm-clerical, Farming-fishing, Transport-moving, Priv-house-serv, Protective-serv, Armed-Forces.
relationship: Wife, Own-child, Husband, Not-in-family, Other-relative, Unmarried.
race: White, Asian-Pac-Islander, Amer-Indian-Eskimo, Other, Black.
sex: Female, Male.
capital-gain: continuous.
capital-loss: continuous.
hours-per-week: continuous.
native-country: United-States, Cambodia, England, Puerto-Rico, Canada, Germany, Outlying-US(Guam-USVI-etc), India, Japan, Greece, South, China, Cuba, Iran, Honduras, Philippines, Italy, Poland, Jamaica, Vietnam, Mexico, Portugal, Ireland, France, Dominican-Republic, Laos, Ecuador, Taiwan, Haiti, Columbia, Hungary, Guatemala, Nicaragua, Scotland, Thailand, Yugoslavia, El-Salvador, Trinadad&Tobago, Peru, Hong, Holand-Netherlands.
最终的分类标签有两个:>50K, <=50K.
下一步是分析数据:
1、数据预处理:
由上述的数据集我们得知,Adult数据集的很多个特征值是离散的取值,他们跟连续的取值的特征不同,需要对其取值进行一一映射,让它适应KNN的数值型离散数据的处理条件。为此我们可以构造一个键值对字典,对数据集进行一次扫描来进行替换,使得所有的离散的非数值数据转换为离散数据:
1 def precondition(dataSet): 2 dict={'Private':0,'Self-emp-not-inc':1,'Self-emp-inc':2,'Federal-gov':3, 3 'Local-gov':4,'State-gov':5,'Without-pay':6,'Never-worked':7,
当然这种构造字典的方法是非常愚蠢的,因为我们要写一个非常大的字典,应该考虑下面这种字典构造算法:
1)将每种特征值的离散取值copy到一个文本文件中;
2)读取文本,对于每一种特征,给予一个初始value 0,对于每一种特征的取值,形成一个键值对(key,value)并插入到dict中而后自增value的值
3)将数据集进行替换并将其他的非数值类型转换为数值类型(str→integer)
1 dataSet = [[int(column.strip()) if column.strip().isdigit() else dict[column.strip()] for column in row] for row in dataSet]
2、数据清洗
数据中含有大量的不确定数据,这些数据在数据集中已经被转换为‘?’,但是它仍旧是无法使用的,数据挖掘对于这类数据进行数据清洗的要求规定,如果是可推算数据,应该推算后填入;或者应该通过数据处理填入一个平滑的值,然而这里的数据大部分没有相关性,所以无法推算出一个合理的平滑值;所以所有的‘?’数据都应该被剔除而不应该继续使用。为此我们要用一段代码来进行数据的清洗:
1 def cleanOutData(dataSet):#数据清洗 2 for row in dataSet: 3 for column in row: 4 if column == '?' or column=='': 5 dataSet.remove(row)
这段代码只是示例,它有它不能处理的数据集!比如上述这段代码是无法处理相邻两个向量都存在‘?’的情况的!修改思路有多种,一种是循环上述代码N次直到没有'?'的情况,这种算法简单易实现,只是给上述代码加了一层循环,然而其复杂度为O(N*len(dataset));另外一种实现是每次找到存在'?'的列,回退迭代器一个距离,大致的伪代码为:
1 def cleanOutData(dataSet): 2 for i in range(len(dataSet)): 3 if dataSet[i].contain('?'): 4 dataSet.remove(dataSet[i]) ( dataSet.drop(i) ) 5 i-=1
上述代码的复杂度为O(n)非常快速,但是这种修改迭代器的方式会引起编译器的报错,对于这种报错可以选择修改编译器使其忽略,但是不建议使用这种回退迭代器的写法。
2、数据归一化:
思考这样两组数据:
A(1,2,3)
B(2,3,1000)
现在要计算A和B两组数据的距离:√(1-2)2+(2-3)2+(3-1000)2 这样算是没错的,但是是否会产生这样一个问题:第三个属性对于结果的影响太大了?答案显而易见是肯定的。然而这三个属性之间的相关性应该是0,他们应该是相互独立的,那么这种影响就应该被消除,所以我们还应该增加一个归一化数据的过程:
归一化数据的主要方法有很多种,网上有很多很完善的实现,这里我采用的是Min-Max Normalization,它将任意取值范围的特征值转化为0到1区间内的值:
1 def norm(dataSet):#归一化数据,将所有的数据集中在【0,1】中,保证取值比较大的数据对于距离的影响不会太大 2 minVec = dataSet.min(0) #按行取得每个特征的最小值 3 maxVec = dataSet.max(0) #按行取得每个特征的最大值 4 DValue = maxVec - minVec #取得每种特征的最大最小值之差 5 normData = zeros(shape(dataSet)) #产生一个保存已经标准化的数据的矩阵 6 m = dataSet.shape[0] #取得数据集的行数,即数据的条数 7 normData=(dataSet - tile(minVec,(m,1)))/ tile(DValue,(m,1)) #normData = (unNormData - min) / (max - min)
8 return normData
上述代码比较难以理解的地方在于min/max这两个方法的返回值?其实dataSet的类型不是Python自带的列表类型,而是Numpy模块中的array类型,min(max)函数的返回值是压缩其参数axis的维度取得最小值(最大值)的结果,即axis = 0时,取的是第0维的arr[0][0][0],arr[1][0][0],arr[2][0][0]……arr[n][0][0]中的最小值作为min[0],arr[0][0][1],arr[1][0][1],arr[2][0][1]……arr[n][0][1]中的最小值作为min[1],以此类推来取得dataSet中每一列的最小值(最大值)。
tile函数返回的是参数列表的重复,即tile(Arr,N)返回的是一个一维列表,其组成为Arr矩阵的N次重复,tile(Arr,(m,n))返回的是一个二维列表,其组成为m行向量,每个向量为Arr的n次重复。
3、数据集读入
读入数据集就是上述数据预处理+数据清洗的过程:
1 def createDataSet(filename): 2 with open(filename,'r')as file: 3 dataSet = [line.strip().split(',')for line in file.readlines()] 4 del(dataSet[-1]) 5 cleanOutData(dataSet) #数据清洗 6 dataSet=precondition(dataSet) #数据预处理 7 labels=[each[-1]for each in dataSet] #获取最后一列数据,获得类别标签 8 dataSet=[each[0:-2]for each in dataSet] #去除最后一列数据,获得无分类数据 9 return array(dataSet),labels #重点:返回的是Numpy.array类型
KNN的分类过程并不需要用到每种特征的特征名,如age/fnlwgt等,而决策树(Decision Tree)是需要用其计算信息增益的。类别标签的保存可以为后续使用测试算法来进行测试该算法的正确率的时候使用。
三、训练算法
KNN并没有训练算法的过程。它没有一个独立的分类器,所形成的分类器会对输入的向量进行一次“全扫描”的距离计算,然后得出类别,它不像决策树那样生成一棵独立的树,可以运用到几乎所有特征属性相同的数据集中。所以KNN的训练时间为0,但是其测试时间为N。
四、测试算法
KNN的训练算法几乎是“特异”的,针对一个分类任务我们要构造一个分类器,它很难进行模块化并形成一个接口。但是它的过程几乎是一模一样的,如上所述:
使用KNN算法将某个向量划分到某个分类中的过程如下:
1)计算训练集中的每个向量和当前向量之间的距离;
2)按照距离递增排序;
3)选择与当前向量距离最小的前k个向量;
4)计算前k个向量中每个类别的频率;
5)选择出现频率最高的类别作为新向量的分类。
根据这个过程我们来构造伪代码:
首先我们写针对一个向量的情况的分类算法:
1 def classify(vector,dataSet,testLabels,labels,k): 2 for vec in vector: 3 distance = sqrt(abs(((tile(vec,(dataSet.shape[0],1)) - dataSet) ** 2).sum(axis = 1))); #计算距离 4 sortedDistance = distance.argsort() 5 dict={} 6 for i in range(k): 7 label = labels[sortedDistance[i]] 8 if not label in dict: 9 dict[label] = 1 10 else: 11 dict[label]+=1 12 sortedDict = sorted(dict,key = operator.itemgetter(1),reverse = True) 13 return sortedDict[0][0]
这段代码的难点在于第3行和第12行的代码:下面我们一一来解释:
1)计算距离的式子是被我写长了,其实拆开来写非常好理解:
√(x1-x2)²+(y1-y2)²+(z1-z2)² = √ (v1 - v2) ² 这里的v1和v2是向量而不是值
tile(vec,(dataSet.shape[0],1))构造了一个长度和dataSet相等的矩阵,它每一行(每个向量)都是vector的某一行(在这个程序中就是vector本身),然后将这个矩阵和dataSet相减,得到的就是一个每一行都是测试集与该向量的距离的向量的矩阵,然后就是常规的向量平方求距离,然后求和,然后取开平方的过程。
2)sortedDict = sorted(dict,key = operator.itemgetter(1),reverse = True)
emmm其实在Python3的环境中这条语句是有Error的哈哈,因为dict无法进行排序😄,所以这句代码应该修改为:
1 sortedDict=sorted(dict2list(dict),key=operator.itemgetter(1),reverse=True)
即将dict转换为一个list来进行排序:
1 def dict2list(dic:dict):#将字典转换为list类型 2 keys=dic.keys() 3 values=dic.values() 4 lst=[(key,value)for key,value in zip(keys,values)] 5 return lst
返回一个“推测”出来的标签是没有什么作用的,return sortedDict[0][0]返回的即是vector的推测分类,不妨我们修改return语句为:
return sortedDict[0][0] == testLabels[j] 这里的j是跟随着迭代次数而增加的。
这样我们获取到的是一个Boolean类型的值,它表示当前的向量的“预测分类”和“实际分类”是否相同,那么我们就需要一个函数来迭代这些向量给这个classify函数:
1 def testClassify(testDataSet,dataSet,testLabels,labels,k): 2 j = 0 3 for vec in testDataSet: 4 if classify(vec,dataSet,testLabels,labels,k,j) == True; 5 #预测正确 6 else: 7 #预测错误 8 j += 1
增加这一层函数调用其实多此一举:
1 def classify(testDataSet,vector,testLabels,labels,k): 2 j = 0 3 correct = 0 4 for vec in testDataSet: 5 distance = sqrt(abs(((tile(vec,(vector.shape[0],1))-vector)**2).sum(axis=1))); #计算距离 6 sortedDistance = distance.argsort() 7 dict={} 8 for i in range(k): 9 label = labels[sortedDistance[i]] 10 if not label in dict: 11 dict[label]=1 12 else: 13 dict[label]+=1 14 sortedDict= sorted(dict,key=operator.itemgetter(1),reverse=True) 15 if sortedDict[0][0] == testlabels[j]: 16 #预测正确,正确计算次数+1 17 correct += 1 18 j += 1 19 return correct/len(testDataSet)
到这里我们就能得到一个分类算法的正确率了。运行一遍看看结果:
选择k=1 / 3的情况(因为Adult数据的官方给出的错误率用的就是k =1 / 3的两种情况)
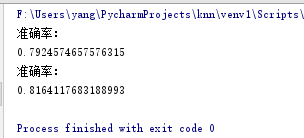
上面一个是k = 1 的情况,下面那个是k = 3的情况,对比官方数据:(官方给的是错误率不是正确率)
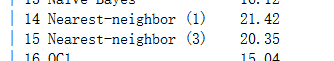
emmm我觉得还行哈哈,最后做一个测试,不做数据归一化的情况:
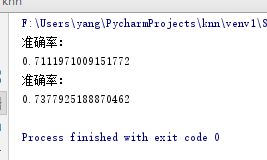
没眼看哈哈
五、完整代码
跟着上面写,给完整代码不存在的,拒绝伸手。
六、算法总结
这一节就先写到这里,下一节是KNN的现实意义和实际运用,作为一个专家系统来说,KNN非常简单便捷,对于脏数据的反应不大、不敏感,但是它的计算的复杂度非常高。在上面的每一段代码都是可以运行的(除了dict无法排序的陷阱哈哈),不过还是没有贴出来完整代码,伸手党太多了哈哈。上面提到的大部分是在学习KNN中遇到的难点,有问题可以跟我讨论哦~原创不易,转载注明出处:https://www.cnblogs.com/DawnSwallow/p/9428132.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号