网络流(dinic算法)

网络最大流（dinic）

模型

在一张图中,给定一个源点s,给定汇点t,点之间有一些水管，每条水管有一个容量，经过此水管的水流最大不超过容量，问最大能有多少水从s流到t（s有无限多的水）。

解法

dinic算法通过不断寻找增广路的方法得到最大流。

增广路：从源点开始通过一些边到达汇点的边集称为一条增广路。

显然，通过一条增广路的水流是有最小限制的，其就等于增广路上水管最小的通过量。

通过寻找一条条增广路，每次找到后经过的边权都减去最大流量，并将答案加上最大流量，就得到了部分解。

但是部分解不一定是最优的，因为程序不存在反悔机会。比如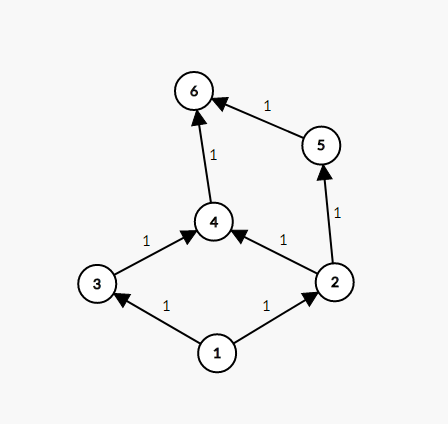

对于此图来说如果先找到的增广路是1->2->4->6,在下一次寻找中,1->3->4然后就会发现无路可走了，得出的答案就是1，实际上如果走1->2->5->6和1->3->4->6答案为2，显然更优。

所以，我们在找到一条增广路后需要将经过的路径反向建边构造反悔的路径如图

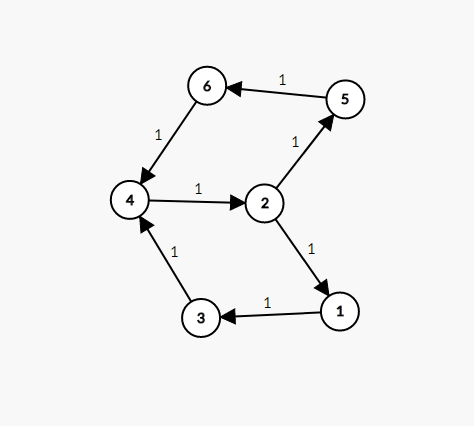
这是第一次增广选择1->2->4->6之后，对于经过的边反向建立反悔边，如果此时继续寻找增广路，就会选择1->3->4->2->5->6。这两条路径相结合，实际上就是走了1->2->5->6和1->3->4->6这两段。所以在寻找完增广路后反向建边，可以使答案不出问题。

但是这样的做法其实是EK算法，它会被某些特殊数据卡住。如图

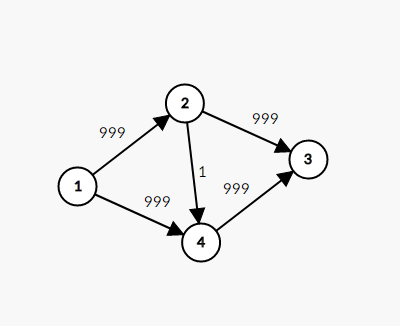
第一条增广路为1->2->4->3,如图（红色为反向边）

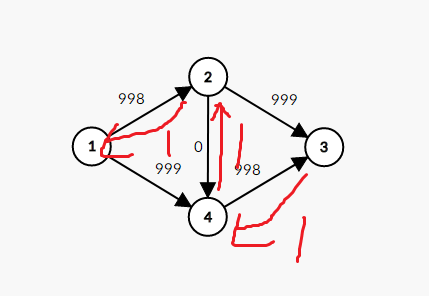
此时的增广路为1->4->2->3，然后就陷入了循环，一共要做999*2次才能做完，效率非常的低。

所以就要一个分层图的方法来解决，也就是Dinic算法。

以源点为初始点，根据边便利全图并且打上层数标记，（能遍历的边流量要>0,以保证能增广到此处），判断此图是否仍有增广路径的依据即为汇点是否被遍历过。然后以此基础重复以上求增广路的算法，每次只能从一层走向下一层的点，这样就有效避免了问题。

举个栗子

就此图来说，1,2,3,4的层数分别为1,2,3,2。所以在求增广路的时候就会直接走1->2->3,而不会重复走了（2不会走向4，因为层数相同）。

然后这就是Dinic算法的大致过程了，还有些优化的算法（如当前弧优化）也可以使用，不过影响不大。

#include<bits/stdc++.h>
#define inf 1e9
using namespace std;
const int maxn=200005;
int n,m,s,t,a,b,c,tot;
int deep[maxn],nex[maxn],las[maxn],lnk[maxn],cost[maxn],q[maxn];
int read()
{
	int ch=0,x=0;while(ch=getchar(),ch<'0'||ch>'9');
	while(x=x*10+ch-48,ch=getchar(),ch>='0'&&ch<='9');
	return x;
}
void add(int x,int y,int z){nex[++tot]=y;las[tot]=lnk[x];lnk[x]=tot;cost[tot]=z;}
int bfs(int s,int t)//求层数 
{
	memset(deep,0,sizeof(deep));
	int head=1,tail=1;q[1]=s;deep[s]=1;
	while(head<=tail)
	{
		int u=q[head];
		for(int k=lnk[u];k!=-1;k=las[k])
		if(!deep[nex[k]]&&cost[k]>0)//必须能有流量才遍历 
		{
			deep[nex[k]]=deep[u]+1;
			q[++tail]=nex[k];
		}
		head++;
	}
	return deep[t];//判断是否能找到增广路 
}
int dfs(int now,int t,int limit)//求解增广路 now表示当前点，t表示汇点,limit表示当前流量 
{
	if(now==t||!limit)return limit;
	int flow=0,f;
	for(int k=lnk[now];k!=-1;k=las[k])
	{
		if(deep[nex[k]]==deep[now]+1&&(f=dfs(nex[k],t,min(limit,cost[k]))))
		{
			limit-=f;
			flow+=f;//flow表示这个点增广的最大流量 
			cost[k]-=f;cost[k^1]+=f;//建反向边 
			if(!limit)break;//若当前流量都可以得到分配，就退出。 
		}
	}
	return flow;
}
int dinic(int s,int t)
{
	int ans=0;
	while(bfs(s,t))ans=ans+dfs(s,t,inf);
	return ans;
}
int main()
{
	n=read();m=read();s=read();t=read();
	memset(lnk,-1,sizeof(lnk));tot=-1;//边从-1开始记，这样保证一条边x的反向边即为x^1，比较好操作 
	for(int i=1;i<=m;i++)a=read(),b=read(),c=read(),add(a,b,c),add(b,a,0);
	printf("%d",dinic(s,t));
	return 0;
}