网课-数据结构学习笔记2

---

---

树状数组

局限性：若区间信息不可减（即无法由两个前缀信息推出），树状数组就显得力不从心了。

• P6225 [eJOI2019] 异或橙子

  Trick：异或具有交换律、结合律，可拆开考虑每个位置的贡献。

• P3372 【模板】线段树 1

  算法：区修区查树状数组

  核心思想是将式子拆开，维护 $\sum c[i]$ 与 $\sum c[i]\ast i$。

  Trick：拆分式子，独立维护项。

• P6619 [省选联考 2020 A/B 卷] 冰火战士

  算法：树上数组上倍增

  Trick：关于值域的问题就考虑维护关于值域的桶。

---

---

线段树

基础

by @ducati:

（这是一个卡空间技巧。）

• P3401 洛谷树

  神奇 $O({\log }^{3}n)$ 题目。

  首先重链剖分。然后拆二进制位分别统计。接着我们需要求出异或和为 1 的区间个数。

  然后就成了“最大子段和”模型：统计区间前缀、区间后缀、区间本身，然后做匹配。

  Trick：异或拆位、“最大子段和”模型。

• P4198 楼房重建

  Trick: Push_up 不一定得是 $O(1)$ 的。

• P7453 [THUSCH2017] 大魔法师

  Trick：矩阵乘法简化懒标记合并

  由于矩阵乘法满足结合律、分配律，我们可以用矩阵懒标记维护区修区查向量区间和。

---

权值线段树

权值线段树与线段树的结构完全相同，基本操作也相同。二者的主要区别在于：前者维护了序列区间信息，后者维护了桶相关信息。

• 线段树二分

• 线段树合并

  1. 判空

  2. 子节点合并

  3. 向下递归

  均摊时间复杂度。

  • 例题：P6773 [NOI2020] 命运

    线段树合并优化树形 DP。（挺不爽的当时讲这个题的人给提示让直接想线段树合并但实际应该提示先想 $O(n^2)$ 做法让我以为这是裸的数据结构题 :(，然后这道思维题我就什么都没有练到。）

    好吧实际你仔细推一下这个树形 DP 部分就也还好。

• 线段树分裂

  将权值线段树 T 分为 ≤ k 的部分 T1 和 > k 的部分 T2。最多建立 $O(\log n)$ 个新节点。

---

可持久化线段树

注意空间时间都带 $\log$。

• P4137 Rmq Problem / mex

  $\text{mex}$ 操作与值域、最值密切相关，考虑在值域线段树上二分。于是发现在每个节点中记录最大的左端点即可。

  Trick：值域线段树记录最近出现下标

• The Classic Problem

  Trick：主席树维护高相似度版本、线段树上哈希 + 二分优化前缀比较。

  做的时候不要脑抽了，实际我们只用将主席树所维护的对象看作一个“元素”，剩下的操作和普通 Dijkstra 是一样的。

• 二维数点

  离线可以用扫描线。

  在线可以用主席树。

  带修则可以使用树套树。

---

线段树优化建图

用于优化将边连向连续编号节点的情况。

• Legacy

  其实说来非常简单。如图，叶子节点为图上节点，如图所建出来的结构即为从 $15$ 到 $[7,13]$ 所有节点建了一条边。

  

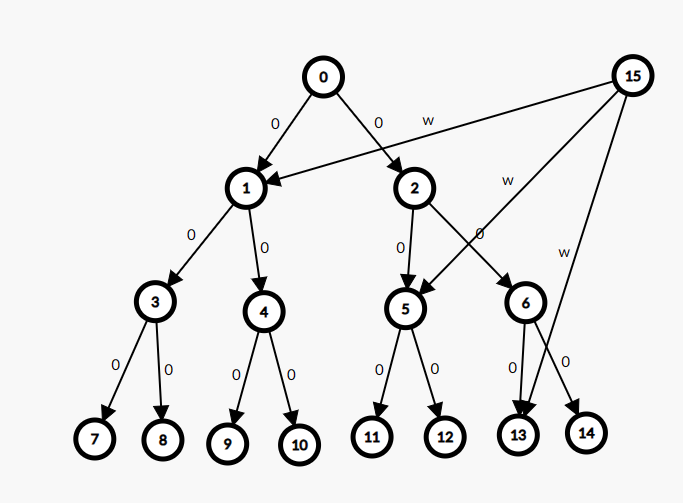
实现上需要注意线段树除最后一层的节点，总数可能达到第一个大于等于 $n$ 的二正整数次幂。

---

线段树分治

核心思想：

1. 将 难以维护的“删除” 操作去除，换为容易维护的“加入”操作的逆操作——“撤销”。同理，如果加入难维护删除易维护，我们也可以考虑线段树分治。

2. 离线，利用线段树对时间段做分治，并引入 标记永久化。

需要注意的是，由于“撤销”的存在，我们不能优化均摊复杂度数据结构。（为什么？& 为什么启发式合并不是均摊复杂度？）

• P5787 二分图 /【模板】线段树分治

  如果只有加边的操作，可以用 扩展域并查集 维护。但并查集是出名的无法删除的数据结构，考虑线段树分治。

  由于线段树分治不能优化均摊复杂度数据结构，我们此处应当使用 启发式合并，而非路径压缩。

• P5227 [AHOI2013] 连通图

  我是傻缺这是很明显的线段树分治啊！

---

树套树

被用于解决动态在线二维数点问题。

主要有：线段树套线段树、树状数组套线段树（主席树）、线段树套平衡树（有时平衡树可以用 map、set 替代）。

---

---

分块

实际想到使用分块有这么一个提示：如果一道题的暴力既可以 $O(n)$ 修 $O(1)$ 查，也可以 $O(1)$ 修 $O(n)$ 查，那么就可以考虑分块。

---

序列分块

其中前两个操作，就是查询、询问中一个做前缀和，一个直接做查询。

第三个操作就是朴素的分块。

第四个操作就是将区间加转化为差分，再转化为前两个操作。

• 例一：

  

  • 朴素思路：每个块维护一个有序序列，每次查询时做二分，时间复杂度 $O(n\sqrt{n}\log n)$。

  • 归并：在修改时，如果对块边角进行操作，不用将其所在块直接全部重排，而是将进行了操作的部分 + 没进行操作的部分进行归并，于是修改时间复杂度消除 $\log n$。

  • 调整块长：设块长为 $T$，修改时间复杂度为 $O(T+\frac{n}{T})$，查询时间复杂度为 $O(T+\frac{n}{T}\log n)$，故 $T=\frac{n}{T}\log n$ 解得 $T=\sqrt{n\log n}$。

• 例二：

  

  Trick：均摊复杂度

  为什么不能直接用颜色段均摊？

• 例三：P4117 [Ynoi2018] 五彩斑斓的世界

---

值域分块

没有例题？

---

操作分块

操作分块主要被用于解决这样的一类问题：

1. 插入/删除新元素需要重构整个数据结构。

2. 插入/删除一个元素的贡献对于某个特定询问可以快速计算。

3. 或者说，询问也需要离线，以便调换顺序计算。

于是其大体的操作步骤如下：

1. 设定阈值 $B$，每 $B$ 个操作为一个块，进行如下步骤：

2. 枚举每一个询问操作。如果询问也需要离线的话，调换枚举顺序。

3. 对于每一个询问操作，枚举时间在其之前的块内修改操作，其贡献加上原数据结构贡献就是答案。

4. 将所有修改操作放入数据结构，重构。

• 例一：

  

  （上面的 $k$ 为一较小常数。）

  这道题属于“一个修改操作的贡献对于某个特定询问可以快速计算”类型。

• 例二：P5443 [APIO2019] 桥梁

  这道题还用到了可对询问离线的性质。

---

树上分块

• May Holidays

  实际基本和前面的“数列分块入门 2”是一样的。然而由于本题的整体加减较为特殊，仅为 $+1/-1$，故我们可以通过“合并相同点权，指针移动找 0 点”的方法做到每次 $O(1)$ 块查询，故有总复杂度 $O(n\sqrt{n})$。

贪心方法：找到当前最深而还未被标记的点，将从它开始向上跳 $\sqrt{n}$ 次跳到的节点记为一个关键点，然后标记关键点 $\sqrt{n}$ 距离以内的所有节点。

这个东西有什么用？我们通过这些关键点建立虚树，每个点内储存从其到其父亲的信息。

---

---

莫队

基础

莫队的关键就在以极短的时间快速转移到相邻状态，一般是 $O(1)$。

【注意：莫队不一定只能解决区间询问！】

例：

（可用递推式展开 $(\genfrac{}{}{0ex}{}{n}{m})=(\genfrac{}{}{0ex}{}{n-1}{m})+(\genfrac{}{}{0ex}{}{n-1}{m-1})$。）

---

树上莫队

---

回滚莫队

• 歴史の研究

• P5906 【模板】回滚莫队&不删除莫队

• P8078 [WC2022] 秃子酋长：用链表，做不插入莫队。

  Trick：链表是不支持插入的数据结构（或许可以出到线段树分治上？），链表的关键词为“相邻”“前驱”“后继”。

---

莫队二次离线

将插入一个点的贡献拆为差分（？），再次离线下来，再用数据结构计算。

---

---

树上问题

树上差分

• 边差分、点差分

• 路径操作转为最后的子树统计

• 例题：P1600 [NOIP2016 提高组] 天天爱跑步

  Trick:

  1. 将路径拆为“向上”“向下”两段。

  2. 拆开式子中的变化项，化为几个不变项之间的关系统计。

  3. 当做信息满足可减性的子树统计时，可以只用一个桶扫然后做差分。

---

DFS 序

可以发现，在一棵子树当中的所有点的 dfs 序都是连续的，且子树的根结点的 dfs 序是最小的。因此容易用一个区间表示出一棵子树的所有 dfs 序。

---

重链剖分

• P4092 [HEOI2016/TJOI2016] 树

  Trick：将链上问题转化为子树问题，以更快更容易地维护。

• P5305 [GXOI/GZOI2019] 旧词

  Trick:

  1. 轻重儿子分类维护。利用重链剖分的结构以及重儿子的唯一性，将轻重儿子的信息分开维护的方式。（实际 DDP 也使用了这个思想。）

  2. 扫描线解决一维限制。（扫描线不一定是扫区间，遇到任意难办的一维限制时都可以尝试扫描线。）

---

长链剖分

• P5903 【模板】树上 K 级祖先

  $O(n\log n)$ 预处理，$O(1)$ 单次查询做法。

  

• Dominant Indices

  Trick：长链剖分优化深度有关统计问题。

  有显然 $O(n^2)$ DP。

  其实这里的思路与 dsu on tree 是很相似的：一条长链共用一个 DP 数组，每次合并将轻儿子贡献合并进数组。由于每条长链至多被合并一次，时间、空间复杂度 $O(n)$。

  本质上这个方法是怎么实现优化的？。。。不知道（为什么一定要保证是长链？）

---

树上启发式合并

处理子树信息。

先递归计算所有轻儿子，并不记录它对当前子树的贡献；递归计算重儿子，继承它对当前子树的贡献。然后暴力遍历除重子树以外子树所有节点，计算贡献。

时间复杂度 $O(n\log n)$。

• 板子：Lomsat gelral

---

点分治、边分治、点分树

这类算法主要被用于解决树上“整体性”比较强的一类问题。

点分治

P3806 【模板】点分治 1

P4178 Tree

处理路径 / 连通块信息。

本质原理：“树上任意一条路径 / 连通块都可以分为‘经过根’、‘不经过根’两种。”

每次递归选取树的重心，然后递归处理去掉重心后的每个连通块。递归层数不超过 $O(\log n)$。

边分治

没看懂他说的用来替代边分治的方法。

点分树（动态点分治）

P6329 【模板】点分树 | 震波

如果每次询问都重新建出一次点分治结构，容易发现是很冗余的。

于是我们在点分治每次选取的重心之间连边，建出一棵新的树结构，称其为“点分树”。它具有如下两条性质：

1. 它的高度与点分治的深度一样，只有 $\log n$ 级别。

2. 对于任意两点 $u,v$，它们在点分树上的 LCA 一定在它们在原树的路径上。

于是每次做询问操作时，考虑枚举每一个 $x$ 的祖先作为 LCA 的情况。

对于每一个点 $x$，维护一棵线段树，每个下标表示子树中 $dis(x,y)$ 的点权和。为了减去重复，我们还需要对每个 $so{n}_x$ 也维护其子树中 $dis(x,y)$ 的点权和。

---

---

离线分治(?)算法

CDQ 分治

• CDQ 分治本质上优化了什么？想起来 lyd 之前在蓝书中所写的：“CDQ 的本质是将一个动态问题转化为了一个静态问题，而这往往会使问题更简单。”

• 什么情况下使用 CDQ？@吾王美如画：“一定要归纳到偏序关系上。”

• P3810 【模板】三维偏序（陌上花开）

  如何写四维偏序？...

• P4169 [Violet] 天使玩偶/SJY摆棋子

  Trick：

  1. 拆绝对值。

  2. 将时间维纳入考虑转化为三维偏序（经典 CDQ 题型）。

• P2487 [SDOI2011] 拦截导弹

  CDQ 优化 1D/1D DP。

  Trick：

  1. “左 - 中 - 右”的递归顺序。DP 问题中需保证一个位置在做贡献之前，其必须已经做完了所有的查询。

  2. 线段树、树状数组都可以直接维护最大值数量。

• P8253 [NOI Online 2022 提高组] 如何正确地排序

  Trick：对于难以直接计算而有很多计算部分重复的式子，我们可以考虑每一个元素对最终答案做了多少“贡献”。

---

整体二分

$k$ 大数查询是经典的应当应用二分的问题。

• P3332 [ZJOI2013] K大数查询

  没太看懂为什么需要线段树？——你是傻缺吗，这里是区间操作，当然要线段树。

• P3242 [HNOI2015] 接水果

  做这道题的时候我在第一步就卡住了。。。

  首先要通过（可能有分类讨论）将它转化为一个二维数点问题。

  然后有两种方法：

  1. 扫描线一维，然后做另一维 + 权值维的树套树。

  2. 整体二分，再扫描线一维，就转化为了上一题的模型。

---

线段树分治

up

---

二进制分组

二进制分组主要被用来将 “动态”问题转化为“静态”问题，即将一个带插入的问题转化到一个不支持插入、不支持删除的数据结构也能做。

主要思想是这样的：假设当前数据规模为 $n$，我们按 $n$ 的二进制表示将其分为多组二的幂次大小的数据。当新增一个数据时，我们从最低位开始，如果当前位为 1，那么就将这一位的数据拿出来，一起向上进位；如果当前位为 0，我们就可以将进位过来的数据在这一位进行重构。（这个过程就好像 2048 的感觉，就是在模拟二进制加法进位。）由于每一个数据最多被放入 $O(\log n)$ 次新的数据组，设构建一个规模为 $n$ 的数据组的复杂度为 $O(f(n))$，则总复杂度为 $O(f(n)\log n)$。

但使用这个方法的条件实则很苛刻。首先信息须满足可加性；其次，因为上面的复杂度实际是均摊的，我们并不能直接维护删除，故如果存在删除操作信息须满足可减性。

譬如 String Set Queries。这道题要求我们做动态 AC 自动机，然而 AC 自动机可视作一个静态的数据结构。

---

---

K-D Tree

在线、小空间解决 矩形加、矩形查询 问题，预处理 $O(n\log n)$，单次操作时间复杂度 $O(\sqrt{n})$。

但对于圆查询、最近点对之类的问题，它的复杂度并没有保证。

• 时间复杂度证明（今天终于听懂了）：

  考虑询问一个矩形时，时间复杂度等于访问到的 K-D Tree 子节点个数，故我们可考虑该矩形与 K-D Tree 中矩形子节点的关系：

  1. 完全无交。我们不可能访问到这一类节点。

  2. 完全被包含在询问矩形内。

  3. 部分相交。

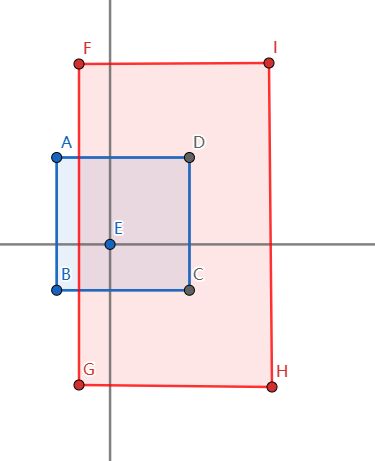
  我们来随意观察一个 3 类矩形（下图蓝）与询问矩形（下图红）。由于蓝矩形的儿子节点不好考虑是竖着分还是横着分，我们直接考虑其孙子。此时可以发现：孙子中最多有两个 2 类矩形两个 3 类矩形。推广结论，则有：

  • 访问到的 2 类矩形的个数最多为 3 类矩形的两倍。因此算出 3 就算出了 2。

  • 访问到的 3 类矩形个数满足递推式：$T(n)=2T(n/4)+1$，使用主定理解得 $T(n)=O(\sqrt{n})$。

  

---

---

总结

• 静态：询问操作必须在修改操作之后。与之相对的概念为“动态”。

• 离线：一般来说我们要修改执行询问的顺序时会离线。与之相对的概念为“在线”。

一些我认为可称为“弱化条件”的算法：

算法	作用	条件
线段树分治	将“删除”操作化为“插入”和“撤销”	可以插入，询问在线（在仅存在插入操作的前提下）
操作分块	线段树分治能做的它都能做；以一个中和的时间复杂度对询问“离线”	可以插入
CDQ 分治	将“动态”化为“静态”；解决偏序问题	修改操作之间相互独立，即贡献得满足可加性
整体二分	实际也是三维偏序，CDQ 分治在值域问题上的特例（以值域为第一维，而非以时间维为第一维的 CDQ 分治）	同上
二进制分组	化静态为动态，化插入为重构	信息须满足可加性；存在删除操作信息须满足可减性
莫队	高维空间点问题	相邻状态之间可以快速转移

可用于求偏序问题的算法/数据结构：CDQ 分治、树套树、扫描线、KD-Tree。