网课-计算几何、线性代数、博弈论学习笔记2

线性代数

高斯消元

（注：上述结论的前提是进行了完全的高斯消元。）

• Vasya and Shifts

  将 $q$ 次高斯消元中的 $b$ 放在一起做即可。（矩阵求逆一题也可以用类似思路解决。）

  Trick：同时进行多个相似矩阵高斯消元。

• P3232 [HNOI2013] 游走

  高斯消元解决随机游走经典题。

• DZY Loves Games

  太好了又可以水一道黑

  1. 先将答案写作矩阵快速幂形式，推出需要解决陷阱房之间概率情况。

  2. 用 CF832E 的 Trick 优化高斯消元。

• Random Walk

  先考虑暴力高斯消元，发现过不去。

  考虑 主元法，以期望次数确定的 $t$ 节点为根，然后求出所有节点关于 $t$ 的一次函数即可。

---

线性基

再补充几个：

5. 求第 $k$ 大的：（？）

6. 对于每个能过够表出的 $x$，有几种表出方案：方案数即为 $2$ 次方的自由元个数。

• P3292 [SCOI2016] 幸运数字

  树上路径建立线性基。需要用到线性基合并...

• P4151 [WC2011] 最大XOR和路径

---

行列式、矩阵树定理

行列式我推荐之前 skc 讲的版本：link

矩阵树定理则是 tzc_wk 的表达比较清晰，到时候用的时候直接背结论：

1. 无向图生成树个数：

   

2. 边带权，求所有生成树权值之积的和：

   

3. 有向图生成树个数（需要指定根）：

   

• P4336 [SHOI2016] 黑暗前的幻想乡

  似乎有一个容斥的外壳。

• P6624 [省选联考 2020 A 卷] 作业题

  看到 $gcd$ 我们应当想到用莫比乌斯反演。

  好像有非常巧妙的将“加法 $\to$ 乘法”的做法——一次函数乘积的一次项。

---

---

博弈论

之前写的：link

OI 中所研究的公平组合游戏一般不会存在平局。这时状态可以看作一个 DAG。

---

阶梯 Nim

理解证明了，因为最后一级为 0，是一个偶数，它不能再下放。

阶梯 Nim 的两种形式：

1. 将后一级的石子放到前一级。

2. 正常从每一级拿除石子，但前一级的石子数不能多于后一级。

前者为后者的差分形式（但数组似乎是反着的？）。

• P5363 [SDOI2019] 移动金币

  看了一下大概是有个博弈论外壳的计数 DP 题。

---

---

计算几何

基本向量操作

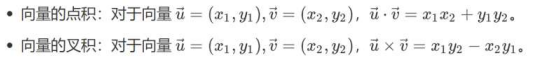
将右手的食指指向 $u$，向 $v$ 的方向转，大拇指向上则 $u\times v$ 为正，反之为负。

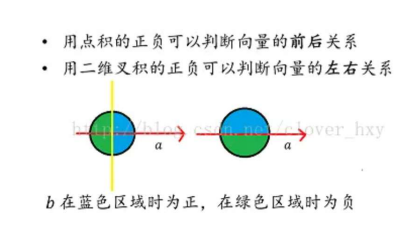
极角从小到大：

---

凸包

• P2742 [USACO5.1] 圈奶牛Fencing the Cows /【模板】二维凸包

  做一遍上凸包，再做一遍下凸包。

闵可夫斯基和

很好的参考资料：@夏天/isummer 的博客

$A,B$ 求和后再求一次凸包，得到 $C$。

从形象的角度理解，可以想象凸包 $A$ 沿着凸包 $B$ 的边向量的方向移动，转了一圈，最终画出的轮廓就是 $C$。见下图，粉色图形即 $C$：

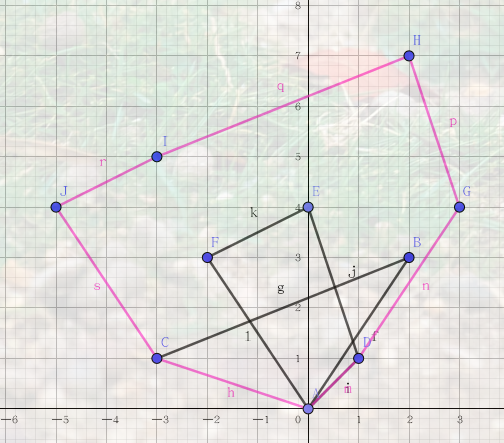
观察到 $C$ 中所有的边不是来自 $A$ 就是来自 $B$，于是我们就可以将 $A,B$ 的所有边向量抽出来进行极角排序得到的结果就是 $C$ 了。

对了，还差一点，这里我们只得到了 $C$ 的轮廓而没有得到其具体坐标。考虑确定其最上端的点，显然 $A$ 的最上端点加上 $B$ 的最上端点就是 $C$ 的最上端点。

这样就做完了！（真的很简洁）

• P8101 [USACO22JAN] Multiple Choice Test P

  这道题涉及到求多个凸包的闵可夫斯基和。而根据我们上面的分析，实际根本不需要两个两个地合并凸包，直接将所有凸包的边抽出来即可。