网课-数论学习笔记2

very good reference

---

---

Miller-Rabin

推荐看我之前写的。

---

---

狄利克雷卷积

• 乘法逆元（求 $f\ast g=ϵ$ 中 $g$ 的前 $n$项）。

  

• $$I=\phi \ast 1$$

  证明：走神没听到。。。

• $$e=\mu \ast 1$$

  证明：发现有平方因子则 $\mu (x)=0$，因此只用考虑每个质因子至多出现一次的情况。那么有 $(\mu \ast 1)(n)=\sum _{i=0}^n(\genfrac{}{}{0ex}{}{n}{i})(-1{)}^i=(1-1{)}^n=[n=0]$。

• $O(n\log \log n)$ 求 $g=f\ast 1$ 和 $g=f\ast \mu$

  有平凡 $O(n\log n)$ 做法。

  先考虑 $g=f\ast 1$。对每一个质数做前缀和，即由 $b\ast p^{k-1}\to b\ast p^k$，等价于做高维前缀和。

  $g=f\ast \mu$ 则可以这么处理：易得有 $f=g\ast 1$，故我们只需要依次 对每个质数做高维差分 即可。

• 积性函数的卷积依旧为积性函数。

  积性函数的逆依旧为积性函数。

  积性函数的复合、点积（$(f\dot{g})(n)=f(n)g(n)$）依旧为积性函数。

---

---

莫比乌斯反演

• 基于约数差分的莫比乌斯反演：

  $$f(n)=\sum _{d|n}g(d)⟺g(n)=\sum _{d|n}\mu \left({\displaystyle \frac{n}{d}}\right)f(d)$$

• 基于倍数差分的莫比乌斯反演：

  $$f(n)=\sum _{n|d}g(d)⟺g(n)=\sum _{d|n}\mu \left({\displaystyle \frac{d}{n}}\right)f(d)$$

如果将每个正整数视为高维点，那么此二者就相当于高维前缀差分以及高维后缀差分。

我们之前一直使用的一种做法本质为：先提出 $gcd$，然后对 $[gcd(i,j)=1]$ 进行反演。但我个人认为这种方法不太能被称为反演，因为它只用了 $e=1\ast \mu$ 这一条性质。

但 nixnehc 提供了一种我认为可称为“正统”的莫比乌斯反演方法。我之所以这么说，是因为它与传统反演的模式很相似：构造一个方便计算答案的 $g$ 函数，一个方便直接计算的 $f$ 函数，然后通过 $g=f\ast \mu$ 来得到 $g$。

---

• $$\sum _{i=1}^n\sum _{j=1}^{n}f(gcd(i,j)),n\le {10}^7$$

  1. $$

     定义 $g$ 满足 $f=g\ast 1$，则：

     $$\sum _{i=1}^n\sum _{j=1}^n\sum _{d|gcd(i,j)}g(d)$$
     $$\sum _{d=1}^{n}g(d)\sum _{d|i}^n\sum _{d|j}^n$$
     $$\sum _{d=1}^{n}g(d){\lfloor {\displaystyle \frac{n}{d}}\rfloor }^2$$

     由于 $g=f\ast \mu$，将 $g(d)$ 展开写的话：

     $$\sum _{d=1}^n{\lfloor {\displaystyle \frac{n}{d}}\rfloor }^2\sum _{t|d}\mu (t)f\left({\displaystyle \frac{d}{t}}\right)$$

     我们可以对 $g(d)$ 做 $O(n\log \log n)$ 的预处理，如果 $f$ 为积性函数也可以线性筛。

  2. $$

     $$\sum _{i=1}^n\sum _{j=1}^n\sum _{d|gcd(i,j)}f(d)[gcd({\displaystyle \frac{i}{d}},{\displaystyle \frac{j}{d}})=1]$$
     $$\sum _{d=1}^{n}f(d)\sum _{i=1}^{\lfloor \frac{n}{d}\rfloor }\sum _{j=1}^{\lfloor \frac{n}{d}\rfloor }[gcd(i,j)=1]$$
     $$\sum _{d=1}^{n}f(d)\sum _{i=1}^{\lfloor \frac{n}{d}\rfloor }\sum _{j=1}^{\lfloor \frac{n}{d}\rfloor }\sum _{t|gcd(i,j)}\mu (t)$$
     $$\sum _{d=1}^{n}f(d)\sum _{t=1}^{\lfloor \frac{n}{d}\rfloor }\mu (t){\lfloor {\displaystyle \frac{n}{dt}}\rfloor }^2$$

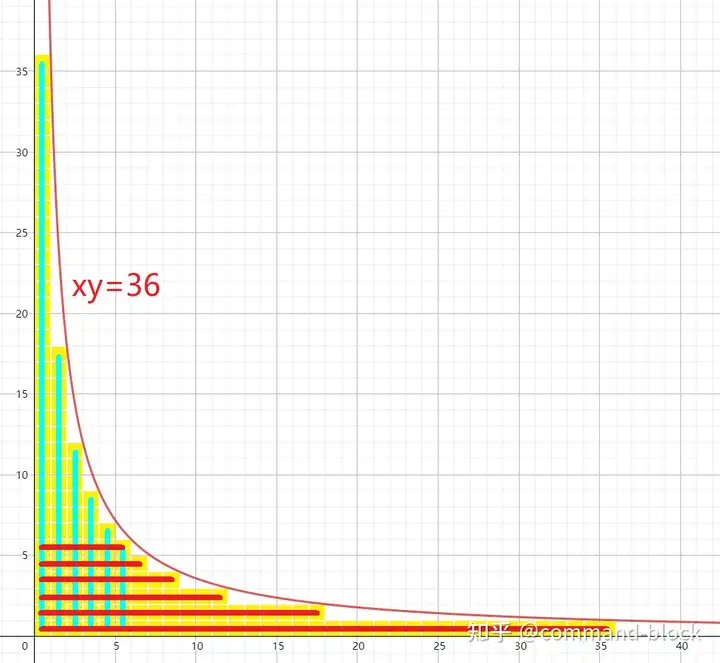
     此时二次数论分块已可解，用普通线性筛预处理 $\mu$ 前缀和之后，能够做到 $O(n)$；然而，可以发现杜教筛会顺带求出所有 基本和组 （见下文）的前缀和，故实际可以做到 $O(n^{\frac{3}{4}})$。（？）

     若再令 $T=dt$，则有：

     $$\sum _{T=1}^n{\lfloor {\displaystyle \frac{n}{T}}\rfloor }^2\sum _{t|T}\mu (t)f\left({\displaystyle \frac{T}{t}}\right)$$

     虽然最后和 1. 是一样的，但 1. 的过程在这道题上显然更加简洁。

---

• $$\sum _{i=1}^n\sum _{j=1}^n\text{lcm}(i,j),n\le {10}^7$$

  转化一下：

  $$\sum _{i=1}^n\sum _{j=1}^n{\displaystyle \frac{ij}{gcd(i,j)}}$$

  1. $$

     令 $f(n)=\frac{1}{n}$，定义 $g$ 满足 $f=g\ast 1$，则：

     $$\sum _{i=1}^n\sum _{j=1}^{n}ij\sum _{d|gcd(i,j)}g(d)$$
     $$\sum _{d=1}^{n}g(d)d^2\sum _{i=1}^{\lfloor \frac{n}{d}\rfloor }\sum _{j=1}^{\lfloor \frac{n}{d}\rfloor }ij$$

     （这一步要注意提出消失的 $d^2$）

     令 $C(n)=\frac{1}{2}n(n+1)$，则：

     $$\sum _{d=1}^{n}g(d)d^{2}C{\left(\lfloor {\displaystyle \frac{n}{d}}\rfloor \right)}^2$$

     再来研究 $g(n)$ 的求法：

     $$g(n)=\sum _{d|n}{\displaystyle \frac{d}{n}}\mu (d)$$
     $$g(n)={\displaystyle \frac{1}{n}}\sum _{d|n}d\mu (d)$$

     后面 $\sum$ 那一块可以用线性筛预处理，总复杂度 $O(n)$。

  2. $$

     $$\sum _{d=1}^{n}d\sum _{i=1}^{\lfloor \frac{n}{d}\rfloor }\sum _{j=1}^{\lfloor \frac{n}{d}\rfloor }[gcd(i,j)=1]ij$$
     $$\sum _{d=1}^{n}d\sum _{i=1}^{\lfloor \frac{n}{d}\rfloor }\sum _{j=1}^{\lfloor \frac{n}{d}\rfloor }\sum _{t|gcd(i,j)}\mu (t)ij$$
     $$\sum _{d=1}^{n}d\sum _{t=1}^{\lfloor \frac{n}{d}\rfloor }\mu (t)\sum _{i=1}^{\lfloor \frac{n}{dt}\rfloor }\sum _{j=1}^{\lfloor \frac{n}{dt}\rfloor }ij$$
     $$\sum _{d=1}^{n}d\sum _{t=1}^{\lfloor \frac{n}{d}\rfloor }\mu (t)t^{2}C{\left(\lfloor {\displaystyle \frac{n}{dt}}\rfloor \right)}^2$$

     二次数论分块可解（剩下同上一题）。令 $T=dt$，则也可以化为 1. 中的式子。

---

• [AGC038C] LCMs

  将最终答案乘以二再加上 $\sum a_i$，则是下面的式子：

  $$\sum _{i=1}^n\sum _{j=1}^n\text{lcm}(a_i,a_j)$$

  为了更方便地处理，我们令 $b(i)$ 表示数字 $i$ 在 $a$ 中出现的次数，则有：

  $$\sum _{i=1}^m\sum _{j=1}^m\text{lcm}(i,j)b(i)b(j)$$
  $$\sum _{i=1}^m\sum _{j=1}^m{\displaystyle \frac{ij}{gcd(i,j)}}b(i)b(j)$$

  就不写 1. 的做法了，反正其实大同小异。

  2. $$

     经过与上一题类似的推理过程，我们能够得到：

     $$\sum _{d=1}^{m}d\sum _{t=1}^{\lfloor \frac{m}{d}\rfloor }\mu (t){(\sum _{i=1}^{\lfloor \frac{m}{dt}\rfloor }b(idt)i)}^2$$

     令 $T=dt$，则有：

     $$\sum _{T=1}^m{(\sum _{i=1}^{\lfloor \frac{m}{T}\rfloor }b(iT)i)}^2(\sum _{d|T}{\displaystyle \frac{T}{d}}\mu (d))$$

     两个括号都可以以调和级数复杂度处理，总复杂度 $O(n\ln n)$。

接下来是几道非套路的莫比乌斯反演题：

---

• $$\sum _{i=1}^{n}gcd(\lfloor \sqrt[3]{i}\rfloor ,i),n\le {10}^{21}$$

  第一步先枚举 $\lfloor \sqrt[3]{i}\rfloor$，因为这个东西的范围 $\le {10}^7$。于是有：

  $$\sum _{i=1}^{\lfloor \sqrt[3]{n}\rfloor }\sum _{j=i^3}^{(i+1{)}^3-1}gcd(i,j)$$

  $gcd$ 有一侧范围太大怎么办？考虑用 辗转相除法 优化啊！于是：

  $$\sum _{i=1}^{\lfloor \sqrt[3]{n}\rfloor }\sum _{j=i^3}^{i^3+3i^2+i}gcd(i,jmodi)$$

  （注：以下部分没有考虑 $(i+1{)}^3-1>n$ 的情况。）

  $$\sum _{i=1}^{\lfloor \sqrt[3]{n}\rfloor }i+(3i+1)\sum _{j=1}^{i}gcd(i,j)$$

  如果你眼力足够好，就已经能看出来这是欧拉反演的一个经典模型了——$gcd$ 求和。我们不妨再推一下：

  1. $$

     设 $f(n)=n$，定义 $g$ 满足 $f=g\ast 1$，根据结论易发现有 $g=\phi$。则有：

     $$\sum _{i=1}^{\lfloor \sqrt[3]{n}\rfloor }i+\sum _{d=1}^{\lfloor \sqrt[3]{n}\rfloor }\phi (d)\sum _{i=1}^{\lfloor \sqrt[3]{n}/d\rfloor }\sum _{j=1}^{\lfloor \sqrt[3]{n}/d\rfloor }(3i+1)$$

     那两个 $\sum$ 显然可以化为等差数列求和公式，然后再随便做一下整除分块即可。（整除分块复杂度为 $\sqrt{n}$，可以做多次询问，或者再加强一下这个问题。）

  2. $$

     懒得推了，到最后你会发现我们可以用 $\mu$ 表示出 $\phi$ 来。

---

• 定义 $F(n)=\sum _{i=1}^n\sum _{j=1}^n[gcd(i,j)+\text{lcm}(i,j)\ge n]$，请对于每一个整数 $i\in [1,n]$ 求出 $ans(i)=\sum _{i=1}^{n}F(i)$。$n\le {10}^6$。

  $\ge$ 不好处理，考虑通过做差分将其化为 $=$。 令 $f(n)=F(n)-F(n+1)$，则有：

  $$f(n)=\sum _{i=1}^n\sum _{j=1}^n[gcd(i,j)+\text{lcm}(i,j)=n]$$

  （明显，如果 $i$ 或 $j$ 满足 $\ge n$，则 $gcd(i,j)+\text{lcm}(i,j)\ge n$。故上式不用考虑 $n+1$。）

  此题用 1. 并不方便处理，故让我们直接尝试 2.：

  $$f(n)=\sum _{d=1}^n\sum _{i=1}^{\lfloor \frac{n}{d}\rfloor }\sum _{j=1}^{\lfloor \frac{n}{d}\rfloor }[gcd(i,j)=1][d+ijd=n]$$

  先不要急着拆 $[gcd(i,j)=1]$，再观察一下：

  $$f(n)=\sum _{d|n}\sum _{i=1}^{\frac{n}{d}}\sum _{j=1}^{\frac{n}{d}}[gcd(i,j)=1][ij={\displaystyle \frac{n}{d}}-1]$$

  容易发现 $i,j$ 的上界可以去掉：

  $$f(n)=\sum _{d|n}\sum _{i=1}\sum _{j=1}[gcd(i,j)=1][ij={\displaystyle \frac{n}{d}}-1]$$

  这里有一个 Trick：求将一个数 $x$ 分成两个互质数相乘的方案数。将 $x$ 质因数分解，设其有 $w(x)$ 个不同的质因子，显然有答案 $2^{w(x)}$。所以有：

  $$f(n)=\sum _{d|n}{2}^{w(\frac{n}{d}-1)}$$

  $w(x)$ 可以轻松线性筛预处理。总复杂度 $O(n)$。

---

---

基本和组

定义 $D(x)=\{\lfloor x/1\rfloor ,\lfloor x/2\rfloor ,\dots ,\lfloor x/x\rfloor \}$ 为 $x$ 的基本和组。

易证其大小为 $O(\sqrt{n})$。

• Trick：$\{\lfloor x/1^k\rfloor ,\lfloor x/2^k\rfloor ,\dots ,\lfloor x/{\sqrt[k]{x}}^k\rfloor \}$ 的大小为？

  运用设定阈值，再做均值不等式的方法。设定阈值 $B$，可以发现 $i>B$ 时都有 $\lfloor x/i^k\rfloor <\lfloor x/B^k\rfloor$，时间复杂度为 $O(B+\frac{x}{B^k})$。当 $B=\frac{x}{B^k}$ 成立时，有最优复杂度 $O(x^{\frac{1}{k+1}})$。

• 杜教筛前置知识：

  1. $D(\lfloor x/a\rfloor )\subset D(x)$

  2. 现已知 $f=g\ast h$，且 $F,G,H$ 分别为 $f,g,h$ 的前缀和。已知 $G(D(n)),H(D(n))$，求 $F(D(n))$：

     $$F(n)=\sum _{i=1}^{n}g(i)H\left(\lfloor {\displaystyle \frac{n}{i}}\rfloor \right)$$

     整除分块优化即可。

---

---

杜教筛

求数论函数前缀和的工具。

欲求 $F$。设计 $h=f\ast g$，其中 $H,G$ 易求。

可得：

$$H(n)=\sum _{i=1}^{n}g(i)F\left(\lfloor {\displaystyle \frac{n}{i}}\rfloor \right)$$

$$g(1)F(n)=H(n)-\sum _{i=2}^{n}g(i)F\left(\lfloor {\displaystyle \frac{n}{i}}\rfloor \right)$$

具体实现：

1. 线性筛预处理到 $n^{\frac{2}{3}}$。

2. 记忆化递归计算答案。这里使用 map。（其实杜教筛复杂度的保证源于数论分块的递归最多只有两层，其余都为重复。）

如此，杜教筛有总复杂度 $O(n^{\frac{2}{3}})$。

上面的是“除法式”。因为我们如果已知 $F,G$，想要求出 $H$ 的话，还有一个类似的式子：

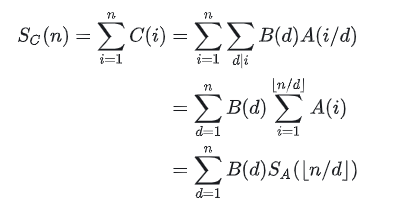
令还有另一种形态：

---

---

gcd 卷积

这里 解释了 gcd 卷积与 min 卷积之间的关系。

---

---

杂 Trick

1. 推导如何用线性筛求积性函数的方法：

   对于 $p^k(k>1)$ 讨论：

   • $p^k|̸x$：直接转移。

   • $p^k|x$：具体分析，甚至有可能需要维护指数等复杂信息。

2. $$\sum _{i=1}^n{\mu }^2(i),n\le {10}^{12}$$

   ${\mu }^2$ 可看作“不含有平方质因子”函数，而这等价于最大的平方因子为 1。故有：

   $$\sum _{i=1}^n\sum _{d^2|i}\mu (d)$$
   $$\sum _{1\le d^2\le n}\mu (d)\lfloor {\displaystyle \frac{n}{d^2}}\rfloor$$

   根据上面的整除分块 Trick，时间复杂度为 $O(n^{\frac{1}{3}})$。

3. $$

   • 约数个数：$d(ij)=\sum _{x|i}\sum _{y|j}[gcd(x,y)=1]$

   • 约数和：$\sigma (ij)=\sum _{x|i}\sum _{y|j}[gcd(x,y)=1]\frac{xj}{y}$

   前者证明：link。

   后者证明实则差不多。我们只需改作将 $p^{b-(c-a)}$ 乘入 $y$，这样 $\frac{j}{y},x$ 就可以看作在 $i,j$ 分别选入的部分相乘。

   更系统的推法是对于每个 $p^k$ 先进行考虑，暴力拆，最后用积性结合。

   

---

---

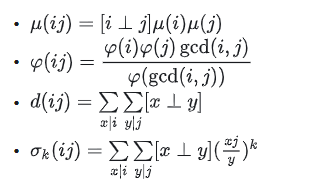
常见积性函数及它们的性质

• $\mu \ast I=ϵ$

• $\phi \ast I=id$

• ${\sigma }_k=I\ast i{d}_k$

• ${\mu }^2(n)=\sum _{d^2|n}\mu (d)$（不具有平方因子函数，这个式子很好理解，相当于取极大平方因子检查是否为 1）

若 $C$ 为完全积性函数，则有：

$$(A\cdot C)\ast (B\cdot C)=(A\ast B)\cdot C$$

---

---

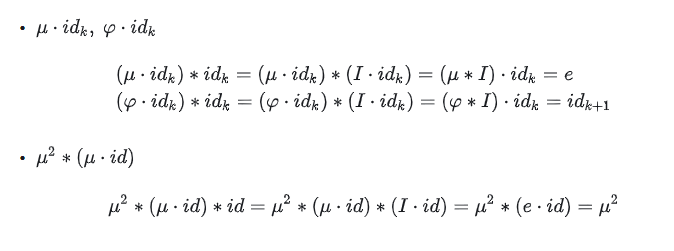
贝尔级数

注意这个东西和狄利克雷生成函数是不同的。它只在积性函数上有定义。

有性质：对于完全积性函数 $f$，有 $f(p^k)=f(p{)}^k$，故其贝尔级数为 ${\displaystyle \frac{1}{1-f(p)x}}$。

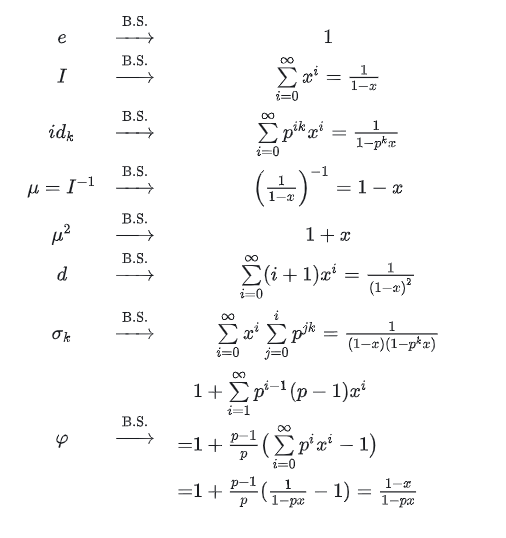
$w$ 函数表示 $n=xy$ 且 $x\mathrm{\perp }y$ 的方案数；$\lambda$ 的组合意义我看不出来。但可以发现，$\lambda$ 为完全积性函数。

---

---

Powerful Number 筛

Powerful Number：每个素因子次数 $\ge 2$。

Powerful Number 可写作 $x^2{y}^3$ 的形式。

。。。。啊吧啊吧啊吧