网课-组合数学学习笔记2
基础
插板法
\(n\) 个无标号物品分成 \(m\) 个有标号组。
-
非空：
\[\dbinom{n-1}{m-1} \] -
有空：
\[\dbinom{n+m-1}{m-1} \]构造 一一对应的转化：
现有两个集合 \(A,B\)。如果所有 \(A\) 中的元素都能够映射到 \(B\) 中，则 \(|A| \le |B|\)；反之，如果 \(B\) 能映射到 \(A\)，则 \(|B| \le |A|\)。二者同时成立，则 \(|A| = |B|\)。
-
组大小有上界：
考虑容斥。（二项式反演型容斥。）
容易将赢的场次转化为连续段内点。然后就容易通过上面的方法得到 \(\le K\) 的解法。最后用 \(\le K\) 减去 \(\le K-1\) 即可。
Catalan 数
wrpwrp 给出了一个特别妙的证法：
Catalan 数的一种表示方式为，从网格图的 \((0, 0)\) 位置，每次向上 / 向右走，走到 \((n, n)\) 且始终不会碰到直线 \(y = x+1\) 的方案数。
研究不合法的路径：
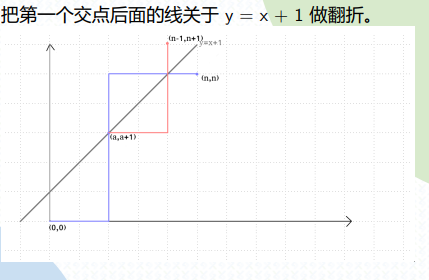
发现所有不合法的路径可唯一映射到一条 \((0, 0) \rightarrow (n-1, n+1)\) 的路径。易得。
这个方法被称为“折线法”。
-
用刚刚的证法再做一遍即可。
折线法进阶：
-
如果形如 \(f[i][j]\) 的 DP 转移方程比较简单，可以考虑换到网格图上做数路径。
斯特林数
-
第一类斯特林数
把 \(n\) 个不同元素构成 \(m\) 个无标号非空圆排列的方案数。
\[\begin{bmatrix} n \\ m\end{bmatrix} = \begin{bmatrix} n-1 \\ m-1\end{bmatrix} + (n-1)\begin{bmatrix} n-1 \\ m\end{bmatrix} \] -
第二类斯特林数
把 \(n\) 个不同元素划分 \(m\) 个无标号非空子集的方案数。
\[\begin{Bmatrix} n \\ m\end{Bmatrix} = \begin{Bmatrix} n-1 \\ m-1\end{Bmatrix} + m\begin{Bmatrix} n-1 \\ m\end{Bmatrix} \] -
普通幂转下降幂
\[m^n = \sum_{i=0}^m \begin{Bmatrix} \min(n,m) \\ i\end{Bmatrix} m^{\underline{i}} \]-
例一：Cards
-
例二
一种方法是咔咔咔用斯特林数推式子，可以做到 \(O(k^2)\)。
如果使用 拉格朗日插值，则可以做到 \(O(k)\)。
拉格朗日插值：如果我们有如果我们有一个 \(n\) 次多项式的 \(n + 1\) 个不同的点值 \((xi, yi)\)，我们可以通过拉格朗日插值公式还原这个多项式。
\[f(k) = \sum^n_{i=0} y_i \prod_{i \ne j} \dfrac{k - x_j}{x_i - x_j} \]证明：如果默认结论“\(n+1\) 个点值即可确定一个 \(n\) 次多项式”结论成立，那么我们构造的 \(f(k)\) 显然有次数为 \(n\) 且有点值 \((x_i, y_i)\)。
回到这道题，有一个结论：
\(\sum^n_{i=1} i^k\) 为一个关于 \(n\) 的 \(k+1\) 次多项式。
证明：使用数学归纳法。假设 \(\sum^{n-1}_{i=1} i^k\) 可表示为一个关于 \(n-1\) 的 \(k+1\) 次多项式 \(T(n-1)\)，满足 \(T(x) = \sum_{i=0}^{k+1} a_ix^i\)。那么如果 \(T(n) = \sum^n_{i=1} i^k\) 要成立，则 \(T(n) = T(n-1) + n^k\) 即 \(\sum_{i=0}^{k+1} a_in^i = n^k + \sum_{i=0}^{k+1} a_i(n-1)^i\) 应当有解，而这的确是有解的。
一个费解的点是：为什么不是关于 \(n\) 的 \(k\) 次多项式？如果是这样，则方程 \(\sum_{i=0}^k a_in^i = n^k + \sum_{i=0}^k a_i(n-1)^i\) 应该有解；而最高项系数，则应有 \(a_i = a_i + 1\)，这显然是错误的。
现在我们只需要求出 \(n = 1,2,\dots,k+2\) 时的点值，代入拉格朗日插值公式即可计算。直接暴力套公式是 \(O(k^2)\) 的，但由于我们代入的 \(x_i\) 是连续的，连乘的结果可以用阶乘表示，于是预处理阶乘后可以做到 \(O(k)\)。
-
杂题
-
[AGC013D] Piling Up（代表元）
-
-
容斥。
-
矩阵快速幂。
-
对于任意一个序列，其差分序列与之构成双射。
-
容斥 & 反演
基本容斥
令 \(P_i\) 表示“满足某种性质的元素的集合”。
左侧：具备至少一种性质的元素个数。
右侧（第一个 \(\sum\) 内）：至少具备 \(S\) 中所有性质的元素个数。
使用时，我们常常使用其来求解“不具备任何性质的元素个数 = 全部元素 - 具备至少一种性质的元素个数”。
证明见下方“Trick：推容斥系数”。
-
容斥优化 排列计数 问题。
本题有朴素状压做法设 \(f[i][j][S]\) 表示第 \(i\) 个点的编号为 \(j\)，且其子树的编号选法为 \(S\)。有子集枚举复杂度 \(O(n^3 3^n)\)。
注意到我们枚举子集的目的实际是为了避免重复编号。于是可以做容斥，钦定必须在 \(S\) 中选取编号。
*另外我还有一个想法，我们能不能钦定哪些边不在图中呢？——不好处理边之间的相对位置关系。
-
Trick：推容斥系数
有什么用？当 \(f_i\)（即容斥系数）不好求时，我们能够将不同的 \(C_0\) 代入，然后高斯消元求解。
我们先拿它来证明最基本的容斥。考虑每一个元素 \(x \in \bigcup^n_{i=1} P_i\)，它对于容斥最终结果的贡献应当为 1。设 \(x\) 一共在 \(k\) 个不同的集合中，\(C_i\) 表示 \(x\) 在 \(i\) 个集合中同时出现的情况，则有：
\[\sum_{i=1}^k \dbinom{k}{i} f_i \]再由二项式定理得：
\[\sum_{i=0}^k \dbinom{k}{i} (-1)^i = \sum_{i=0}^k \dbinom{k}{i} (-1)^i = (-1+1)^k = [k = 0] \]故令 \(f_i = (-1)^{i+1}\)，则有：
\[\sum_{i=1}^k \binom{k}{i} (-1)^{i+1} = -(-1 + \sum_{i=0}^k \binom{k}{i} (-1)^i) = 1 \]
构造条件 \(C_i\) 表示至少 \(i\) 个数在相同位置上，并代入不同 \(C_0\) 表示恰好 \(m\) 个位置在不同位置上。
\[\sum_{i=0}^m \dbinom{m}{i} f_i = a_m \]这里可以直接 \(O(n^2)\) 递推解出 \(f_i\)。
关于反演：
二项式反演
以第一个式子的证明为例。推导过程难点在一开始设出一个式子：
然后代入这个重要的式子：
接着咔咔咔推一下就可以了。
考虑上面二项式反演的组合意义。后者拥有更加常用的组合意义，即 \(g_k\) 表示钦定选择 \(k\) 个、其它任选的方案数，\(f_k\) 表示恰好选择 \(k\) 个；前者则用“错排”来解释比较合适，\(g_n\) 表示 \(n\) 个人随便站的方案数，\(f_n\) 表示恰好 \(n\) 个人都站错的方案数。
子集反演
其实这两个式子，前者代表 \(F\) 为 \(G\) 高维前缀和，后者代表 \(G\) 为 \(F\) 高维差分。（这可以称为定义式。）
高维差分的计算方式实际与高维前缀和一模一样，是逐位做减法。
这次证明代入的关键式为：
其它与二项式反演大同小异。
-
P6442 [COCI2011-2012#6] KOŠARE
同样，子集反演也可以用于“恰好”与“至多 / 至少”的转换。
-
没太懂。我认为直接称之为容斥 DP 会更合适，考虑一条边加 / 不加入，然后分成若干连通块。过会儿推一下。
min-max 反演
-
设 \(t_i\) 表示第 \(i\) 位变为 \(1\) 的时间，答案等价于 \(E(\max_{i=0}^{n-1} t_i)\)。
使用 min-max 反演。
\[E(\max_{i=0}^{n-1} t_i) = \sum_{S \in [1,n]} (-1)^{|S|+1} E(\min_{i \in S} t_i) \]而 \(E(\min)\) 是很好求的因为可以贪心。
斯特林反演
-
例题一：
设 \(f(n, m)\) 表示只限制行不等价的情况下的方案数，则有：\(f(n, m) = (c^m)^{\underline{n}}\)。
设 \(f(n, m)\) 表示行、列都不等价的情况下的答案，则有：
\[f(n, m) = \sum^m_{i=1} \begin{Bmatrix} m \\ i \end{Bmatrix} g(n, i) \]相当于枚举等价类。
Tips：以后做组合计数问题，可以先弱化问题，然后找弱化后式子和要求式子的关系。
-
图上问题经常的套路就是将“连通”给容斥 / 反演掉。
设 \(f_i\) 表示恰好有 \(i\) 个联通块的方案，\(g_i\) 表示钦定 \(i\) 个子集的方案（求解方法：将图划分为 \(i\) 个子集，子集内随便连边，子集间不连边）（注意不等同于 \(f_i\) 的后缀和），有如下式子成立：
\[g_k = \sum^n_{i=k} \begin{Bmatrix} i \\ k \end{Bmatrix} f_i \]\[f_1 = \sum^n_{i=1}(−1)^{i−1}(i − 1)!g_i \]接下来需要求出 \(g_i\)。这时可以直接枚举子集的划分情况，划分种类数为 贝尔数（即第二类斯特林数的一个前缀和），然后计算连边方案数（使用线性基计算自由元个数）。
生成函数（GF）
多项式定理
多项式 \((x_1 + x_2 + x_3, · · · , x_t)^n\) 的展开式中 \(x_1^{n_1} x_2^{n_2} \cdots x_t^{n_t}\) 的系数
是：\[\dfrac{n!}{\prod_{i=1}^t n_i!} = \dbinom{n}{n_1, n_2, \dots, n_t} \]其中 \(\sum n_i = n\)。
广义二项式定理
上指标反转可以在 \(n < 0\) 时用于将上指标化为正形式。
幂级数展开
使用平凡广义二项式定理即可展开的：
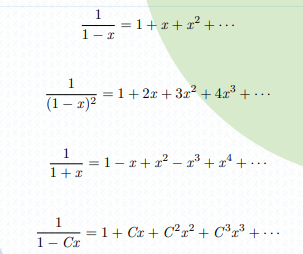
观察 \(\frac{1}{1-x}\) 与 \(\frac{1}{(1-x)^2}\)，猜想：
在 GF 中，乘上 \(\frac{1}{1-x}\) 等价于做前缀和，乘上 \((1-x)\) 等价于做差分。而乘上形如 \(x, \frac{1}{x}\) 的项则是将下标左右平移。
使用泰勒公式展开的：
OGF
-
例一：
正确性是由于若干括号相乘，等价于每个当中挑一个相乘，将所有方案相加。
-
就我最菜，连因式分解和完全立方公式都想不到
:(\[(a+b)^3 = (a+b)(a^2+b^2-ab) = a^3+3a^2b+3ab^2+b^3 \]
EGF
更确切地说，EGF 主要被用于处理若干序列的合并问题。
为什么这么说呢？举例：
-
例一：
仅含偶数项的 EGF：
\[G(x) = 1 + \dfrac{x^2}{2!} + \dfrac{x^4}{4!} + \cdots = \dfrac{e^x + e^{-x}}{2} \] -
例二：
应用
-
推导数列通项公式
例，斐波那契、卡特兰。
-
多项式操作
三个：多项式求逆、多项式 ln、多项式 exp。
\(O(n \log n)\) 复杂度方法见 此。
如果遇到不卡 \(O(n^2)\) 的情况，我们可以对其求导后推一个简单的递推式。
-
例题
-
例一：
生成函数的设计
实际有几种选择：
-
以每种长度的骨牌为单位，构建选择几个骨牌的 EGF。
-
以选了几个骨牌为单位，构建选择每种骨牌的 OGF。
经过实践选择后者更加简洁。
注意不能有 \(A_0 = 1\)，因为可能会导致前面的项与后面的项有重复方案。
有答案的生成函数为：
\[\sum_{i=0}^n A^i(x) = \dfrac{1}{1-A(x)} \] -
-
例二：
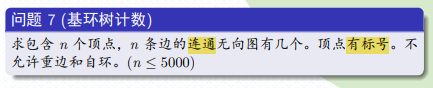
考虑枚举环，将若干棵树拼到环上。
根据 Prufer 定理，\(n\) 个点有标号无根树的数量为 \(n^{n-2}\)；故有 Cayley 定理，\(n\) 个点有标号有根树的数量为 \(n^{n-1}\)。所以有有根树的 EGF 为：\(A(x) = \sum{n \ge 1} \frac{n^{n-1}x^n}{n!}\)。
接着枚举环。注意，这里的环翻转、旋转都会重复，故根据 Burnside 定理，长度为 \(k\) 的环的数量为 \(\frac{k!}{2k}\)。因此答案的 EGF 为：
\[ans = \dfrac{1}{2} \sum_{k \ge 3} \dfrac{A^k(x)}{k} = -\dfrac{1}{2} \ln(1 - A(x)) - \dfrac{A(x)}{2} - \dfrac{A^2(x)}{4} \]（为什么不能直接像下一题，城市规划，那样做？）
-
这道题不同于前两道的一点在于，我们需要自己构造一个生成函数。（类似于反演题目。）
设 \(g[n]\) 表示 \(n\) 个点有标号无向连通图数量，\(f[n]\) 表示 \(n\) 个点有标号无向图数量，可以发现有：
\[F = e^G \]于是求 \(F\) 的多项式 \(\ln\) 即可。
-
