网课-动态规划学习笔记2
“DP 是一种算法,一个工具,而非一种题型。这也是为什么有时候很难分辨一道题要用 DP 还是用贪心,因为你确实很难直接从题面判断要用什么工具。”
“DP 的核心在于设计状态。独立设计一个好的状态可能较为困难,但我们可以根据学过的通用状态进行拓展,得到当前的状态。”
类别
记忆化搜索
记忆化搜索是一种 DP 的实现方法。
相同点:
-
DP 中同一局部问题只计算一次——搜索的记忆化
-
不处理对答案没有贡献的情况——对应搜索的剪枝
不同点:
-
遍历顺序优化复杂度。
-
按数组顺序进行的 DP,经常可以配合一些优化技巧进一步降低复杂度。
数位 DP
经典数位 DP 的要素:求 l 到 r 之间的符合限制的数的个数(或求和),通常这个限制与数位有关。
数位 DP 的主要思想是,把大整数看成一个由 \(0 \sim 9\) 构成的整数序列而不是一个数。并采用序列 DP 的方式,从高位到低位一位一位地 DP。
我之前在 进阶动态规划学习笔记 中写到需要拼凑 + 预处理。实际如果 去掉预处理 一步会更为简单。而且 从高位到低位 会更加简单。
状态大概设计为 \(f[i][j][lim][zero]\),表示第 \(i\) 位为 \(j\)、是否卡上界、前面位是否全为 0。转移从高位到低位,枚举下一位是什么即可。
- 给定 \(l, r\),求 \(l \sim r\) 中有多少个每一位互不相同的数。(\(l,r\) 为 \(k\) 进制数,\(l,r \le k^{150}, k \le 150\))
设 \(f[i][j][lim]\) 表示当前在第 \(i\) 位,并已经确定了 \(j\) 位的值(除了前导 0),并且是否卡上界。
容易发现转移仅与 \(j\) 相关。(\(\leftarrow\) 发现仅与 xx 相关这一步真的很关键!!!)
状压 DP
重要思想是 压缩等价状态。多数情况下,我们是把阶乘级的搜索状态变为指数级的 DP 状态,即忽略元素顺序,记录元素集合。而常用的实现方法是用二进制数来表示集合。
__builtin_ctz:整数后缀 0 个数。
__builtin_clz:整数前导 0 个数。
__builtin_popcount:整数 1 的个数。如果要计算
long long,须写作__builtin_ctzll。
-
P3052 [USACO12MAR] Cows in a Skyscraper G(子集 DP)
-
\(O(3^n)\)
引理:令 \(S\) 为 \(\{1, 2, \dots , n\}\) 的一个子集,\(T\) 为 \(S\) 的一个子集,则不同的 \((S, T)\) 对的个数为 \(3^n\)。
证明:对于每一个元素,它只有三种可能:既不在 S 中也不在 T 中,在 S 中但不在 T 中,既在 S 中也在 T 中。根据乘法原理,总的方案数即为 \(3^n\)。
因此如果 枚举每一个子集进行转移复杂度能做到 \(O(3^n)\)。
简易程序实现:
for(T = S; T; (--T) &= S)。 -
\(O(2^n)\)
尝试将每次加入一个子集改作每次加入一个物品。发现“组数 + 剩余空间”这个二元组可以贪心,直接做即可。
-
-
P1879 [USACO06NOV] Corn Fields G(轮廓线 DP)
常规思路是一行一行地考虑问题。可以有两个优化:用位运算优化判合法时间、预处理合法状态减少枚举数。
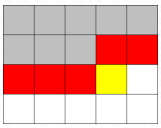
另外可以用 轮廓线 DP。主要思想是逐个加入方格,维护需要关心的轮廓线的状态,如下图我们需要维护红色格子的状态。设 \(f[i][j][S]\) 就是当前最后一个填的第 \(i\) 行第 \(j\) 个格子,轮廓线状态为 \(S\),时间复杂度 \(O(n^2 2^n)\)。
-
P4590 [TJOI2018] 游园会(DP 套 DP)
资料里都说 DP 套 DP 的本质实际是“自动机上 DP”。
回忆一下自动机是什么?“是一个数学模型,或者说一个图,它其中的每一个节点都代表着一个‘状态’,每条边代表的是一个‘转移’,然后我们从自动机中给定的某个起点开始,将一个序列中的元素逐个插入自动机,然后根据元素选择转移,从一个节点走到下一个节点。”
自动机有一个天然的优势,那就是对于任何一个起点,不管我们是怎么从起点走到它的,它的后续转移都是完全相同,这与动态规划的“状态合并”的思想完美吻合。于是在自动机上 DP 是很自然的,如 AC 自动机上 DP、SAM 上 DP 等等
接下来我们要做的就是构建一个“关于奖章串的 LCS 自动机”。研究 LCS DP 的过程,发现每当我们插入一个兑奖串新字符时,DP[i-1] 这个一维数组会变为 DP[i]。那么考虑将 DP[i] 作为一个自动机状态。再由于 0 <= DP[i][j]-DP[i][j-1] <= 1。我们可以将 DP[i] 用其差分数组表示,压缩为一个二进制数即可。(一个数组与其差分 / 前缀和数组构成双射。)
概率 DP
-
状压 DP。设 \(f[S]\) 表示目前只有集合 \(S\) 中的鱼活着的情况的发生概率。转移时暴力枚举鱼即可。
-
DP 相对编号方法 + 主元法解一元一次方程。
- 几何分布的期望值:进行若干次试验,单次试验成功的概率是 p,失败的概率是 1 − p。那么第一次试验成功的期望时间是 \(\frac{1}{p}\)。(证明:\(\sum^{\infty}_{i=1} i(1-p)^{i-1}p = \frac{1}{p}\))
-
线性性拆解求每个点被选中的概率,即求每个点比其所有前驱先被选的概率。设 \(f_x\) 表示能到达节点 \(x\) 的点数,则有概率 \(\frac{1}{f_x}\)。
图、树、计数 DP
-
可以求出 \(n-1\) 时有几条最长最短路径 \(f[i][j][k]\):有 \(i\) 个点时,最长最短路长度为 \(j\),有 \(k\) 个点为 \(j\)。则 \(f[i][j][k] = \sum \binom{n-1-(i-t)}{t} (2^k-1)^t 2^{\binom{t}{2}} f[i-k][j-1][t]\)(三个系数分别表示:选 \(j\) 个点的标号、选择与上一层连边、选择在同一层内连边)。
看一下题解,\([j]\) 维是冗余的,去掉即可通过。
Tips:
-
当边权为 1 时,可以考虑分层做。
-
写出代码后观察状态是否存在无用维度。
-
先研究特点,然后试探一下,找到一种合适的刻画方式,再 DP。
-
[ABC160F] Distributing Integers
不妨先确定第一个点是什么,然后做换根。可以发现,要求的等价于外向树形图拓扑序计数。
外向树形图拓扑序计数有结论:
\[\dfrac{n!}{\prod^n_{x=1} sz_x} \]也可以写作 DP 形式:
\[f[x] = \sum_{(x,y) \in E} \dbinom{sz_x-1}{sz_y} f[y] \]然后再做一次换根法即可。
Tips:
- 树上 DP 问题,不妨都从“换根法”的角度想想。
-
计数转期望的思想。(这样能够用线性性拆分,思考起来更轻松一些。)
-
“点分治 处理树上连通块问题。”
当时学这个就学得并不很好,而且忘完了(
咕咕咕
-
连续段 DP。用于处理序列问题。基本设法是 \(f[i][j]\) 表示前 \(i\) 个数被分为 \(j\) 段时的情况,然后有三种基本操作:
-
新开一段。
-
加入某一段。
-
合并两段。
其实这个路径的走法和前几天那道 Vim 很像。。。
-
-
-
组合意义
-
只考虑用到的东西的贡献,没有用到的先不考虑。
-
-
P6453 [COCI2008-2009#4] PERIODNI
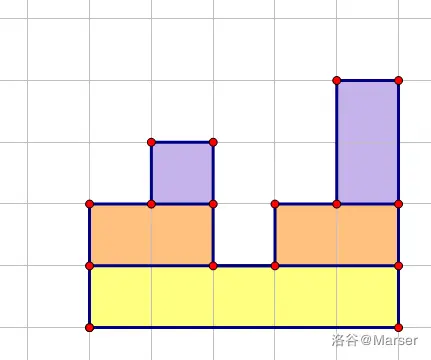
将不规则矩形划分为若干规则矩形,然后依据矩形深度建立笛卡尔树。
-
[ABC321F] #(subset sum = K) with Add and Erase
简单生成函数如 \(\prod (ax + 1)\) 可以在 \(O(n)\) 时间复杂度内实现乘除法。
-
P4645 [COCI2006-2007#3] BICIKLI
DAG 路径计数。
-
设 \(f[i][j]\) 表示 \(i, j\) 之间是否存在回文串,即有 \(O(m^2)\) 暴力。将 \(i\) 的边枚举改为点枚举,能够优化到 \(O(nm)\)。
此题正解最困难的切入点:考虑减少边的数量,使其与 \(n\) 在同一数量级。发现我们想令回文串两端 \(\texttt{0}, \texttt{1}\) 连续段分别对应相等,但由于本图为无向图,我们只需令二者 奇偶性 相等。
那么对于一个同色的连通块,我们只需要用边维持其 连通性 & 奇偶性。如果只有前者,我们可以保留任意一棵生成树;对于后者,我们发现只有 奇环 可能会对其造成影响。于是可以先建出生成树,如果存在奇环,则在任意一个节点上建立一个自环即可。
对于不同的同色连通块构成的图,很容易发现它就是个二分图,直接建出生成树即可。
最后跑一下最开始的暴力即可。
优化
填表法 & 刷表法
-
被动转移(填表法):对一个还未算出值的状态思考其应怎么计算。
-
主动转移(刷表法):将一个已经算出值的状态计算其后继。
数据结构优化 DP
-
“二维偏序的处理方法一般是一维排序,一维使用数据结构处理。”
-
计数 DP 通过拆解项优化复杂度。
-
-
状态设计中剔除可算出状态。
-
拆项后用数据结构维护。
-
-
标算是线段树合并优化 DP。
(我有一个算法,即设 \(f[i]\) 表示强制选点 \(i\) 时它子树内的最大子集。)
其实很多数据结构优化 DP 设计状态都为“恰好”或“钦定”。如果状态设计含有“后/前缀最大”,我们则需要将其化为这个形式。
斜率优化
一般形式:\(f(i) = g(i) + \min_{0 \le j < i} \{h(j) + w(i)v(j)\}\)。
通用做法:set 动态加点维护凸包 / 李超线段树。
但一般由于 \(w(i), v(j)\) 的特殊性,会有更好写的做法。
-
-
方差可写作“平方的均值 - 均值的平方”。
-
特性:\(-v(j), w(i)\) 都递增,可以使用单调队列维护凸包。
-
-
P4655 [CEOI2017] Building Bridges
这道题中 \(v(j), w(i)\) 都没有单调性。
待会儿学了李超线段树再来。link
状态优化
-
P8916 [DMOI-R2] 暗号(费用提前计算)
这一道和我以前做的费用提前计算不太一样,它不是一步将费用算到位的,而是将对未来情况的“预测”编入状态。
-
P6758 [BalticOI2013] Vim(线头 DP)
最后转移部分没有听懂。
-
P7606 [THUPC2021] 混乱邪恶(状态数量优化,随机化优化)
有平凡 \(O(n^3p^2)\) DP 方程,可用 bitset 优化但还是过不了。
发现如果将物品打乱,构造为随机游走问题,则移动范围期望为 \(O(\sqrt{n})\)(证明见:link)。
没有改变状态设计,但通过随机化压缩了状态的范围。
主要思想:发现 DP 方程可以抽象成一个函数,然后对函数进行维护。
-
这里的函数是由若干绝对值函数累加形成的“折线”下凸函数,于是我们可以通过对顶堆维护其斜率。
统计答案时,由于我们只维护了函数的斜率,我们还不能直接还原该函数。需要我们选取一个极端值,它可以快速求出值。


