计算几何学习笔记
点、向量、直线、线段
点、向量
在结构体中储存横纵坐标即可。
向量的加、减、数乘
横纵坐标直接加、减、乘。
点积
-
定义：令 \(\mathbf{A} = (x_1, y_1), \mathbf{B} = (x_2, y_2)\)，二者夹角为 \(\theta\)，则有 \(\mathbf{A}\cdot\mathbf{B} = |\mathbf{A}||\mathbf{B}|\cos\theta = x_1x_2 + y_1y_2\)（结果为标量）。
-
作用：求 \(\mathbf{A}, \mathbf{B}\) 夹角。点积为正，夹角锐角；点积为负，夹角钝角。
叉积
-
定义：令 \(\mathbf{A} = (x_1, y_1), \mathbf{B} = (x_2, y_2)\)，\(\mathbf{A}\) 逆时针旋转 \(\theta\) 到 \(\mathbf{B}\)，则有 \(\mathbf{A}\times\mathbf{B} = |\mathbf{A}||\mathbf{B}|\sin\theta = x_1y_2-x_2y_1\)。
-
含义：标量，表示 \(\mathbf{A}, \mathbf{B}\) 形成的平行四边形有符号面积，其正负满足“右手定则”（即若 \(\mathbf{A}\) 在 \(\mathbf{B}\) 的顺时针方向，则 \(\mathbf{A}\times\mathbf{B}\) 为正，逆时针则为负，这也可以通过将食指指向 \(\mathbf{A}\)、中指指向 \(\mathbf{B}\) 大拇指的方向来判断）。
-
作用：
-
判断向量逆、顺、共线关系。
-
计算平行四边形、三角形面积。
-
向量旋转
设向量 \((x, y)\) 逆时针旋转 \(\theta\) 得到 \((x', y')\)，有：
直线、线段
直线一般使用“点 + 向量” / “点 + 点”储存表示。
线段储存两个端点。
点、直线、线段的关系
-
点与线位置关系
-
点与（有向）直线：用叉积判断逆时针、顺时针、在直线上。
-
点与线段：用叉积判断共线，用点积判断重合。
-
-
点与线距离
-
点与点
-
点与直线：直线上取两点，用叉积求和点形成的平行四边形面积，再除以底边长。
-
点与线段：用点积判断点的投影是否在线段上，再按照“点与直线”或“点与点”的方法计算。
-
-
点关于直线的变换
-
投影：设直线为 \((p_1, p_2)\)，点为 \(p\)，则用点积算出 \(\overrightarrow{p_1p}\) 在 \(\overrightarrow{p_1p_2}\) 上的投影向量，随即算出投影点。
-
对称：求出投影点以后作向量加减法即可。
-
-
线与线位置关系
-
直线与直线的位置关系：用叉积判平行，再用点线关系特判是否共线。
-
线段与线段的位置关系：先特判共线的情况；再用叉积检查两条线段是否都满足“另一条线段的两个端点在异侧”，成立则相交。
-
-
线与线交点
-
直线与直线的交点：
求直线 \(AB, CD\) 的交点 \(E\)：
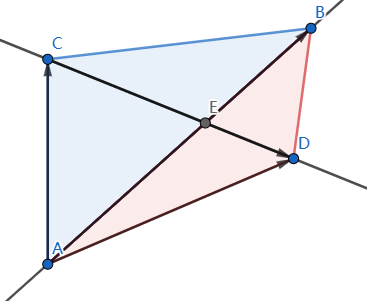
\[\dfrac{x_D-x_E}{x_E-x_C} = \dfrac{y_D-y_E}{y_E-y_C} = \dfrac{|DE|}{EC} = \dfrac{S_{\Delta ABD}}{S_{\Delta ABC}} = \dfrac{\overrightarrow{AD}\times\overrightarrow{AB}}{\overrightarrow{AB}\times\overrightarrow{AC}} \]容易解出 \(E\) 的坐标。
这个方法实质对直线上任意位置关系的 \(A, B, C, D\) 都是成立的，但我不知道怎么证（
-
线段与线段的交点：判断位置关系后转化为直线交点问题。
-
多边形、凸包
旋转卡壳
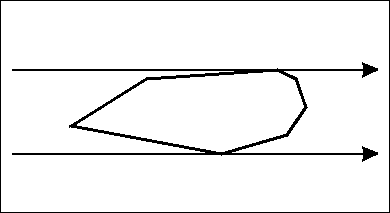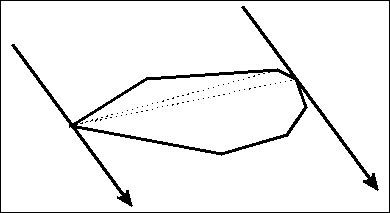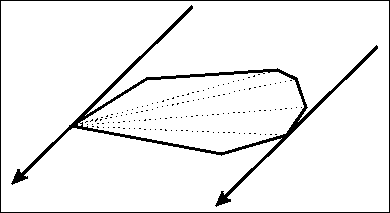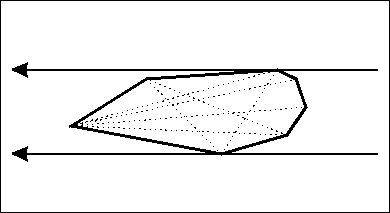
在一个凸包上，某些问题的最优解一定在“边对点”或“点对点”时产生。旋转卡壳的关键就在枚举这对“边点”或“点点”，我们所使用的工具即这对“平行线”——它们能帮助我们找到这些最远的“边点”和“点点”。
