网课-博弈论学习笔记
博弈论证明的关键:必胜态可以到达必败态;必败态只能到达必胜态。
博弈论思考的策略:
-
从小情况出发思考,如 \(n = 2, a_i = 2\)。可以给我们一些灵感
-
打表
-
贪心先找一些性质
Nim 游戏

\(n=2\) 的时候可以用一个巧妙的方法证明:如果两堆石子一样多,则后手可以通过在另一堆上一直模仿先手的行为获胜;如果两堆石子不一样多,则先手可以在第一次取时把两堆变成一样多。这种方法叫做下模仿棋。
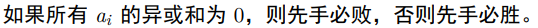
为什么这里面会出现异或?
异或的定义为:
其中,\(a \oplus a = 0\) 为我们选择了异或的关键。
-
例一:Anti-Nim 游戏

\(n=2\) 的情况可以用下模仿棋证明。
结论:
-
当所有石子堆数目都为 \(1\) 时,当且仅当 \(n \bmod 2 = 0\) 时先手必胜。
-
当存在一个石子堆数目 \(>1\) 时,当且仅当 \(a_i\) 的异或和 \(\ne0\) 时先手必胜。
虽然我可以证明,但是我说不清楚是怎么想到这个结论的。
【我有一个不懂的问题:为什么不能想一种办法,直接用 SG 函数刻画 Anti-Nim 问题?】
-
-
分类讨论即可。
SG 函数
-
公平组合游戏:

-
局面的合并:面前有两盘棋,任选一盘下一步。(Nim 中的不同堆)
-
局面的转移:做出决策之后,使得当前局面发生改变。(Nim 中的选石子)
-
定义 \(\text{mex}S\):最小的不在 \(S\) 中的非负整数。
-
定义 SG 函数:
-
当其为必败局面时,SG 值为 0。
-
否则,SG 值定义为它能转移到的所有局面 SG 值的 \(\text{mex}\)。
-
-
性质:两个局面合并后产生的新局面的 SG 值为原先两个局面的 SG 值的异或。
证明方法实则和 Nim 游戏是大同小异的。
-
例一:
如果你没太能理解“局面合并”与“局面转移”的含义,可以看一下这道题。


-
如果将瓶子中的豆子数设计为局面,显然是不现实的。发现瓶子中每个豆子互不干扰,考虑将豆子设计为局面,每次往后加豆子视作局面的合并。最终将所有豆子的 SG 值异或即可。
-
例三:

结束条件为“先切出 \(1 \times 1\) 的人赢”,不符合公平组合游戏的定义。修改规则为“不能切出 \(1 \times k\) 的巧克力块”,不能操作者输。这样就可以用公平组合游戏刻画问题。
平局
此时,状态的转移不再是一个 DAG,而可能出现环。
我们从终止状态出发,倒推出每个状态的胜负情况。对于一个必败态,所有能到达它的点都是必胜态。如果一个点的能到的所有点都是必胜态,则它为必败态。该过程结束后,所有还未确定状态的点即为平局。
阶梯 Nim
“差分”

k-Nim

在普通 Nim 中,异或的实质是每一位相加对 \(2\) 取模。
杂题
这些杂的博弈论题目往往不拘于仅仅拆分局面的套路,而混入了很多“贪心”“DP”的思想。首先你需要有一双会观察的眼睛,实在不行了再启用 SG。
-
ABC278G Generalized Subtraction Gam
-
如果 \(k, n\) 奇偶性相同,划掉对称部分做模仿棋,先手必胜
-
否则 \(l=r\) 且 \(l, n\) 奇偶性不同,\(O(n^2)\) 暴力。
-
-
这个题是对 SG 函数进行树形 DP。对于一棵树,它的局面可以被分裂成“每一棵子树 + 到根节点的一条边”的若干局面,那么这棵树的总 SG 值就等于这些局面的 SG 值的异或和。
若想使用 DP 解决,现在的问题在于:在一棵树的根节点上加一条边,它的 SG 值是如何变化的?我们可以猜想:在根节点上加一条边后的 SG 值是原根节点的 SG 值 +1。考虑断开新边的情况,此时转移到的状态的 SG 值为 0;否则断开原树中的边,转移到的状态是“这条新边 + 原树的一部分”,运用数学归纳法即可证得能够转移到原树所能转移到的每一个状态 +1。
总结一下吧:这道题并没有直接套用 SG 函数的计算方法,而是发现了某些位置之间的 SG 函数的特殊关系。
-
首先需要一个贪心:两人的共同策略是先删 \(\texttt{01}\) 段,再删 \(\texttt{0x}\) 或 \(\texttt{1x}\) 段。故此可以得到:若 \(\texttt{0}, \texttt{1}\) 个数不同,则多者必胜,因为多者总可以使得自己的数量大于少者;若 \(\texttt{0}, \texttt{1}\) 个数相同,则谁先无法进行 \(\texttt{01}\) 段删除谁就必输。
如何求出谁先无法进行 \(\texttt{01}\) 段删除?这就必须用到 SG 函数了(这就不能直接应用贪心算出谁先不能删了,你可以随便画个例子试一下)。本来计算 SG 应当是 \(O(n^2)\) 的,但据说打表出来以后发现有一个长度为 34 的循环节可以 \(O(n)\) 过。
-
由于 \(n\) 的范围过于巨大,我们考虑将白格子设为局面,这样这个题和前面的“分裂游戏”一题就很相似了。
不过这个题麻烦的地方在于它的各个局面之间似乎是互相交错影响的。比如说,当前有两个白格子 \(p, q\),翻转二者,\(\text{lcm}(p, q)\) 是会被它们重复标记的。这是不是意味着我们就不能通过“异或”来合并两个局面的 SG 值了呢?
但实际上,我们可以证明:重复的贡献会被抵消。我们可以把每个白格子 \(x\) 看作独立的局面,且一定有两个局面合并后的结果为二者的异或和。
*点击查看证明*
考虑使用数学归纳法。假设对于 $p, q$,已经有 $SG(p), SG(q)$ 都是按照常规办法计算出 SG 值的,现在要证明的是二者合并后的局面的 SG 值是否等于 $SG(p) \oplus SG(q)$。而证明这条是否成立,即证明 $p, q$ 转移到的重复部分的贡献是否会被抵消。可以证明这么一条引理:
\[(\text{mex}_{i=1}^n a_i) \oplus (\text{mex}_{i=1}^m b_i) = \text{mex}_{1 \le i \le n, 1 \le j \le m} (a_i \oplus b_j) \]说人话,就是 \(\text{mex}\) 关于 \(\oplus\) 满足分配律。这通过公平组合游戏的意义是很好证明的。
既然有了分配律,我们就可以将 \(p, q\) 所能转移到的局面拆出来异或。对于 \(p, q\) 可以转移到的共同局面 \(x\),有 \(SG(x) \oplus SG(x) = 0\)。也就是说 \(x\) 的贡献会被抵消。
证明完了,打个总结吧:其实这里贡献能够被抵消,本质上是因为“翻转”就是“异或”。
最后还需要做一个二次数论分块,很妙。
-
从小情况出发,得到结论,再贪心地用小情况推大情况。


