网课-概率论学习笔记
基本概念
特别地，令 \(A+B\) 表示两个事件的并，令 \(AB\) 表示两个事件的交。（这么多年以来我学概率论一头雾水的很大原因就在于我不知道这一点！！！）
就是概率空间中某个事件在数域上的某种映射。
我们在随机变量上定义一些新运算。令 \(X, Y\) 为两个随机变量，分别表示第一次掷骰子的点数、第二次掷骰子的点数，则 \(X+Y, X-Y, X \times Y, X/Y\) 分别表示两次掷骰子的和、两次掷骰子的差、两次掷骰子的积、两次掷骰子的商；并且对于实数 \(\alpha\)，\(\alpha X\) 表示掷出骰子点数的 \(\alpha\) 倍。
【注意：这里定义的新运算都是对于随机变量这一“函数”的运算，而非对它们的值的运算，并且运算的结果依旧是一个函数——随机变量。】
接下来将“独立”的概念从变量推广到事件。则有：
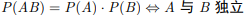
贝叶斯公式
即，在 \(B\) 发生的条件下 \(A\) 发生的概率，可由在 \(A\) 发生的条件下 \(B\) 发生的概率、\(A\) 单独发生的概率、\(B\) 发生的概率推得。
看课件的意思，应该是说这个公式主要被用于在 \(P(A|B) = 1\) 时通过 \(P(B|A), P(B)\) 推导 \(P(A)\)（？）
期望
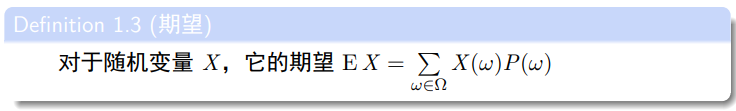
期望是一个作用于随机变量的函数，而且有一些特别的性质。比如，它是一个线性函数：
这个的证明如果搞懂了 \(X+Y\) 的真正含义的话是显然的。（不像我一年多才搞懂它什么意思）
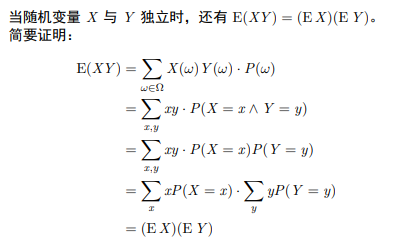
方差
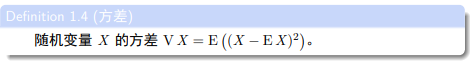
这个定义我属实是说不清它为什么要定义成这样。。。
基本模型
我指的“基本模型”是直接计算期望而用不上 DP 的题型。
如何计算期望呢？首先容易想到用定义直接计算——枚举每种情况并乘上概率。还有一种办法即是用期望的线性性，将它拆为若干位置的期望之和，如果这些位置有随机变量值为 \(1\) 则可等价于它们的概率之和。
-
首先需要知道期望可以用线性性拆分，但不止一种拆分方式。比如这道题，你可以把它拆为 \(\sum_{x=l}^r\text{E}(\sum_{i=1}^n[y_i=x])\)，也可以把它拆为 \(\sum_{i=1}^n\text{E}(\sum_{x=l}^r[y_i=x])\)。
经过实践可以发现，本题中选择前者是更为简单的。这道题需要做一点观察和“组合意义”解说，而不是死推式子。发现其实 \(x_i\) 可以等同于：在掷硬币掷到正面的概率为 \(p\) 的情况下，掷硬币第几次掷到正面。那么 \(y_i\) 可以等同于：在掷到 \(i\) 次正面一共掷了几次。于是 \(\sum_{i=1}^n[y_i=x]\) 也可以等同于：掷 \(x\) 次时掷了几次正面，于是 \(\text{E}(\sum_{i=1}^n[y_i=x]) = px\)，遂有最终答案 \(p(r-l+1)\)。
-
例二
把总期望用线性性拆解为每一次掷出新点数的期望次数之和。
首先，在掷出 \(i\) 种点数后，每次掷出新点数的概率为 \(\frac{n-i}{n}\)。接着再运用一个结论：若某部分在整体中的占比为 \(\frac{1}{p}\)，随机在该整体中取点，则期望在第 \(p\) 次时取到该部分。 即可求得期望再掷 \(\frac{n}{n-i}\) 步掷出新点数。
最后求和，有总期望为 \(n\sum_{i=1}^n\frac{1}{i}\)。
-
例三：P3802 小魔女帕琪
用线性性将总期望拆解为每个长度为 \(7\) 的连续段中每个元素互不相同的概率之和。而又由于每个段的概率相同，只需要求一段的概率，再乘上总段数即可。
-
用线性性将总期望拆解为每个点被“选中”而不是被其它点删除的概率之和。令能到达 \(x\) 的点数为 \(f_x\)，显然有概率 \(\frac{1}{f_x}\)。
-
这道题所用到的方法是最原始的：按照期望定义计算期望，按照“满足要求的方案数除以总方案数”的概率定义计算概率。 但是，在我们做期望 dp、概率 dp、线性展开上头之后，这反而是非常容易被我们遗忘的方法。
另外就是一个求方案数时用到的 “类插板法” 的小技巧。
基础期望/概率 DP
这里是我把树上的 DP 单独列出去了。
期望/概率 DP 存在两点非常特殊之处：
-
通常是倒推的形式。
-
转移方程可能存在后效性，需要用高斯消元/主元法求解。
请结合以下题目理解。
-
例一
对于期望、概率 DP，我们常采用“倒推”的形式，原因可见 知乎-为什么通常期望dp要倒推？。
我们也拿这道题的正推法和倒推法对比一下。如果是正推法，\(f[x]\) 应设为掷了 \(x\) 次连续正面时的期望次数，此时有状态转移方程:
\[f[x] = \begin{cases} f[x-1]+1 & x > 0\\ \sum_{i=1}^n f[x] \times p[x] & x = 0\end{cases} \]而若使用倒推法，则 \(f[x]\) 应设为已经掷了 \(x\) 次连续正面，期望还要掷多少次满足要求，此时有状态转移方程：
\[f[x] = \dfrac{f[x+1]+f[0]}{2}+1 \]肉眼可见，前者还需要维护一个概率 \(p[x]\)，很麻烦。
回到这题采用倒推做法上面。转移式中出现了 \(f[0]\)，存在后效性，因此不能直接算出答案。但是最后我们可以通过 \(f[n] = 0\) 建立一个关于 \(f[0]\) 的方程，得到答案。
-
例二：Fish
由数据范围想到状压 DP，令状态表示当前集合中的鱼活着这种情况的概率。
-
首先，由于是概率 DP，想到倒推。先将 DP 方程加上“剩余人数”一维。
（然后就是我不知道题解是怎么想到的了）设 \(f[i][j]\) 表示剩余 \(i\) 个人时，枪口对准第 \(1\) 个人，让第 \(j\) 个人获胜的概率。接下来要考虑一个人被打死/没被打死之后，该怎么转移状态。这道题的巧妙之处在于，把枪口的移动转化为了编号的移动，压缩了很多状态。 比如，在第 \(1\) 个人进行了一回合后，应该是枪口转向第 \(2\) 个人；但我们也可以将这个过程看作编号的转动：第 \(2\) 个人变为第 \(1\) 个人，第 \(1\) 个人变为第 \(n\) 个人，第 \(k\) 个人变为第 \(k-1\) 个人。-
对于 \(j=1\)，即有 \(f[i][j] = (1-p)f[i][i]\)。
-
对于 \(j\ne1\)，即有 \(f[i][j] = (1-p)f[i][j-1]+pf[i-1][j-1]\)。
接下来，对于每一层 \(i\)，用主元法解方程即可。
-
树上期望/概率 DP
树上期望/概率 DP 和刚刚 DP 不同的地方在于它没有什么要“倒推”的地方了（树上问题怎么会有倒推呢？？？）。
但是，它依旧会存在后效性问题，因为既可能从父亲处更新也可能从儿子处更新。由于根节点没有父亲，它是主要的突破口。基于此，我们主要有两种解决方案：
-
换根 DP。
-
高斯消元/主元法。
-
这个题使用换根 DP 解决了概率 DP 的后效性问题。
-
例二：基本树上随机游走
（这个题能不能从每个出口跑 DP，然后换根？——不太行。如果是这样，还需要特判其它出口不能进入，比较难处理。）
树上随机游走是树上期望/概率 DP 中的一个主要类别。
-
例三：Random Walk
这个题不算比较套路的树上期望/概率 DP。个人认为这个题的关键在将“点的期望经过次数”转化为“有向边的期望经过次数”。结论“出边的经过的期望次数都相同”实际是很反直觉的。这提示我们：
-
在期望、概率问题中，如果换一个角度想问题，经常会推到一些很反直觉但是正确的性质。 这和要依赖直觉再找证明的贪心是不一样的。
-
“转化法”，即将当前期望与更容易求的相关期望进行勾连。
-
-
对于树上情况，就是一个正常的换根 DP。（这里用高斯消元是行不通的。）
对于基环树情况，只需要对环上点进行一次 DP 后再换根即可。
