网课-线性代数学习笔记
线性
一个函数 \(f(x)\) 是线性的，当且仅当：
\(f(x+y) = f(x)+f(y), f(kx) = kf(x)\)
其中 \(c \in \mathbf{R}\)，\(x, y\) 为某种可运算的元素。
向量
纵向的列表。
-
维数：向量的长度。
-
线性函数：
\[f\left(\begin{bmatrix}x_1\\x_2\\\vdots\\x_n\end{bmatrix}\right) = c_1x_1 + c_2x_2 + \dots + c_nx_n \]其中 \(c\) 不一定是数字。
-
线性变换：定义在向量上的线性函数，返回值为向量。
矩阵
一、描述线性变换的方法。
二、若干列向量组成的序列。
-
矩阵乘法：\(f(v) = ABv\)，其中 \(A, B\) 为矩阵。令 \(C = AB\)，即定义了矩阵乘法。
-
单位矩阵：其他位置为 0，主对角线为 1。
-
矩阵快速幂优化技巧：假如是对同一个矩阵多次查询幂，直接乘复杂度为 \(O(qn^3\log v)\)。预处理矩阵的 \(2^k\) 次幂，每次用询问的向量去乘，复杂度可优化为 \(O(qn^2\log v)\)。
矩阵乘法的用处：
-
运用矩阵快速幂实现对同一递推式的加速递推。
-
套用数据结构实现任意区间查询矩阵乘法。
-
套用数据结构动态维护矩阵乘法。
例题：
-
例一
这道题难在设计状态（或者说向量）。实际向量应存入分子和分母，矩阵表达的就是一个通分的过程。
-
矩阵设计方面，很巧，把能塞的都塞进去；卡常部分，使用手动展开矩阵，只存需要的部分。（但好像这道题用单纯的线段树就可以了。。。）
-
这道题体现的是利用矩阵实现双向维护单向信息。因为在套用数据结构后，我们还可以“由右向左”求矩阵积。
-
例四：区间加斐波那契数列，区间查询和
通过矩阵乘法可以转化为区间加同一个数的等比数列，然后就可以用乘法分配律将懒标记转化为一个矩阵加法问题。
-
修改矩阵运算：将 \(+, \times\) 改为 \(\max, +\)，此时单位矩阵主对角线为 \(0\)，其余位置为 \(-\infty\)。
线性基
线性基是在“异或空间”中定义的。如果从高斯消元来理解，它至少是一个上三角矩阵，当然有时也可以把它消成简化梯形矩阵。它主要被用于解决一个集合中任意个数的数异或的最值问题。
-
T441671 0x35-高斯消元与线性空间 - XOR：异或空间中第 \(k\) 小数
这个题要把线性基消成更严格的形式——对于每个 \(p_i\)，它的最高位只有它一个数为 1。消完以后按照 \(k\) 的二进制表示选取即可。
-
时间戳线性基：尽量保留晚插入的向量而继续递归插入早插入的。这样在去除时间戳 \(<t\) 的向量后，可以得到一个 \(\ge t\) 时间戳的线性基。（例：P3292 [SCOI2016] 幸运数字）
【我感觉线性基可以再来点例题。。。】
高斯消元
给定矩阵 \(A\) 和向量 \(B\)，求向量 \(X\) 满足 \(AX = B\)。
高斯消元的本质是三个初等行变换：交换某两行、某个行乘上 \(k\)、加减某个行的 \(k\) 倍，它们本质都是初等矩阵。那么对矩阵进行初等行变换即将 \(AX = B\) 变为 \(PAX = PB\)。当 \(PA\) 为简化行阶梯形矩阵时，非常容易解得 \(X\)。
为了减小精度误差，可以在找消元行时挑系数最大的一行。
-
P4783 【模板】矩阵求逆：有两种理解方式。一种是通过列 \(n^2\) 个同余方程理解；一种是通过 \(AA^{-1} = I\)，然后把 \(A\) 用高斯消元消成 \(I\)，并顺便将 \(A\) 上进行的操作在 \(I\) 上也进行一次。
-
P3265 [JLOI2015] 装备购买：由于高斯消元的策略是“尽量选前面的行”，可贪心地将小的排在前面。
线性空间
-
线性组合：若某个向量能被某组向量表出，称其为这组向量的线性组合。
-
线性空间：一个关于线性组合封闭的集合即为线性空间（向量空间、空间）。
-
\(n\) 维列向量空间：全体 \(n\) 维向量构成的空间。
-
线性无关：称一组向量线性无关，当且仅当其中任何一个向量都不能被其他向量表出。
-
基：对于一组线性无关的向量张成的空间，这组向量称为其的基。
-
维数：该线性空间基的个数。
-
线性变换的新理解：通过一个线性变换，我们会把当前线性空间映射成另一个线性空间（当然也可能不变）。新的线性空间维数不可能大于原先的线性空间。
一句比较拧的话：“对于任意 \(m\) 维的线性空间，都一定存在一个线性变换，把它映射到 \(m\) 维列向量空间。”
看上去就是一句废话。但 \(m\) 维的线性空间其实可能是若干 \(\ge m\) 维的向量的集合。如 \(\begin{bmatrix}1\\2\\3\end{bmatrix}， \begin{bmatrix}2\\4\\6\end{bmatrix}， \begin{bmatrix}3\\4\\5\end{bmatrix}\) 所张成的空间，你可以把它想象成三维空间中一个倾斜的二维平面。
而 \(m\) 维列向量空间则是货真价实的 \(m\) 维向量张成的。如 \(x\) 轴和 \(y\) 轴张成的平面，它在三维中是没有倾斜角的。
所以这一步映射实际是对空间进行了转变的，并不是无意义的。
（下面两个概念是我前面偷懒没写的概念）
-
转置矩阵：将矩阵的行、列交换后的矩阵。记作 \(A^T\)。
-
可逆变换：存在逆的变换（矩阵）。没有全零行的矩阵都满足，初等行变换显然满足。
-
秩：秩是一个矩阵中所有列向量张成的空间的维数。
可以证明初等行变换不改变线性无关的行的数量；并且由于初等行变换为可逆变换，高斯消元后的秩不大于也不小于原来的秩。因此：转置矩阵的秩等于原矩阵的秩。
-
降秩 & 满秩：对于一个矩阵，若所有列向量线性无关则为满秩矩阵，反之则为降秩矩阵。
-
维数公式：设 \(T\) 是从空间 \(V\) 到空间 \(W\) 的线性变换，记 \(\text{ker}T = \{\vec{v}\in V | T(\vec{v}) = \vec{0}\}\) 表示 \(T\) 的核，\(\text{im}T = \{\vec{w}\in W | \exists\vec{v}\in V, \vec{w}=T(\vec{v})\}\) 表示 \(T\) 的像，则有 \(\text{dim}(\text{ker}T)+\text{dim}(\text{im}T) = \text{dim}V\)。（如果一个矩阵为降秩矩阵，则通过它的映射可能会使得空间维数减小。）
此题的关键在于构造矩阵。
可以发现，若构造矩阵 \(E\) 每一个数都为 \(1\)，那么经过 \(AE\) 矩阵中每一个数都变为行之和，经过 \(EA\) 矩阵中每一个数都变为列之和。因此，一次操作的结果为 \(AE+EA\)。
另外还需要发现一个性质：\(E^2 = nE\)。因此再推导一下，就可以把高维的式子可以化到很简计算。
行列式
是一个矩阵的属性，用于描述它将空间（单位面积、体积）放大了几倍。
注解 2：这等于在原本空间的基上加上一个向量。如下图，最终面积等于所加向量围成的面积 + 原面积。
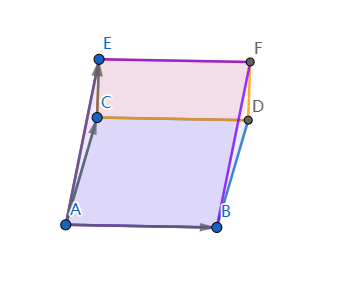
注解 3：那将是一个降秩矩阵，故而显然。
- 将一行数乘后加到另一行上行列式不变。
注解 1：设 \(A, B\) 为两个行向量，则 \(\delta(\begin{bmatrix}A\\B\end{bmatrix}) + \delta(\begin{bmatrix}B\\A\end{bmatrix}) = \delta(\begin{bmatrix}A\\A\end{bmatrix}) + \delta(\begin{bmatrix}B\\B\end{bmatrix}) = 0\)。
注解 2：通过线性展开，我们可以将原矩阵的 \(\det\) 化为若干每行每列只有一个元素的矩阵的 \(\det\) 之和。由于简化阶梯矩阵的 \(\det\) 是很容易求的，我们通过若干次交换行的初等行变换将每个拆开的矩阵化为简化阶梯矩阵，交换次数即 \(\sigma(p)\) 次；又因为交换一次 \(\det\) 就会变为相反数，故有上式。
注解 4：将经受操作的 \(A + k * B\) 那一行线性展开，发现包含 \(k * B\) 的矩阵有两个成比例的行，这说明它是一个降秩矩阵，行列式的值为 0。
其实根据前面可以发现，我们完全可以使用高斯消元求出行列式，那个“排列”不过是定义罢了。具体地说，交换两行行列式取反，加减两行行列式不变，对某行进行数乘则行列式乘上该数，详见 P7112 【模板】行列式求值
还有一条性质：
Matrix-Tree 定理
