网课-组合数学学习笔记

Preface

“用组合意义刻画左右两边，然后发现左右两边讲的是同一个东西。”

“一堆括号乘起来，相当于每个括号里挑一个乘起来，再相加。”

处理求和问题的技巧：当遇到瓶颈时，试着调换 \(\sum\) 的顺序是一个好办法。

---

加法、乘法原理

• 加法原理：同一步之间

• 乘法原理：不同步之间

---

排列

\[A_n^m = \dfrac{n!}{(n-m)!} \]

---

组合

又称二项式系数。

\[\dbinom{n}{m} = \dfrac{n!}{m!(n-m)!} \]

---

下降幂

\[n^\underline{m} = \prod_{i = n-m+1}^n i = \dfrac{n!}{(n-m)!} = \dbinom{n}{m}m! \]

从组合意义上考虑，下降幂和排列数实际是一样的：在 \(n\) 个东西里选出 \(m\) 个东西的排列数。

《具体数学》中是通过和普通幂函数 \(y = x^m\) 进行比较来引出下降幂的。具体地说，定义 \(\text{D}f(x)\) 表示 \(f(x)\) 的微分（即导数），\(\Delta f(x)\) 表示 \(f(x)\) 的差分（即 \(\Delta f(x) = f(x+1)-f(x)\)）。那么 \(y = x^m\) 有 \(\text{D}y = mx^{m-1}\)，\(y = x^{\underline{m}}\) 有 \(\Delta y = mx^{\underline{m-1}}\)，很相像。

此时 \(a\) 的定义域可以达到整个实数域（甚至复数域，但我不清晰）。比如，\((-2)^{\underline{3}} = (-2)\times(-3)\times(-4) = -24\)，\((\frac{1}{2})^{\underline{2}} = \frac{1}{2}\times(-\frac{1}{2}) = -\frac{1}{4}\)。

据下降幂定义的广义二项式系数：对于实数 \(a\) 和非负整数 \(n\)，有：

\[\dbinom{a}{n} = \dfrac{a^{\underline{n}}}{n!} \]

有时候如果 \(\tbinom{n}{m}\) 的 \(n\) 很大而 \(m\) 很小，可以转用下降幂计算。

---

组合数基本公式

对称公式：

\[\dbinom{n}{m} = \dbinom{n}{n-m} \]

加法公式：

\[\dbinom{n}{m} = \dbinom{n-1}{m} + \dbinom{n-1}{m-1} \]

吸收公式（用于求和）：

\[m\dbinom{n}{m} = n\dbinom{n-1}{m-1} \]

三项恒等式：

\[\dbinom{a}{b}\dbinom{b}{c} = \dbinom{a}{c}\dbinom{a-c}{b-c} \]

组合意义：左边代表在 \(a\) 个东西中选出 \(b\) 个东西，再在 \(b\) 个东西中选出 \(c\) 个东西；右边代表在 \(a\) 个东西中选出 \(c\) 个东西，再在剩下的 \(a-c\) 个东西中选出 \(b-c\) 个东西。

---

组合数求和

• 上指标求和：

\[\sum_{i=a}^b \dbinom{i}{a} = \dbinom{b+1}{a+1} \]

代数推导：可使用数归法证明。

组合意义：右边代表在 \(b+1\) 个东西中选出 \(a+1\) 个东西；左边代表枚举第 \(a+1\) 个东西。

• 平行求和：

\[\sum_{i=0}^n \dbinom{a+i}{i} = \dbinom{a+n+1}{n} \]

代数推导：运用对称公式可将平行求和转化为上指标求和。

组合意义：右边代表在 \(a+n+1\) 个东西中选出 \(n\) 个；左边代表枚举前 \(n-i\) 个必选。

---

二项式定理

\[(a+b)^n = \sum_{i=0}^n \dbinom{n}{i} a^ib^{n-i} \]

代入 \(a=b=1\) 得：

\[\sum_{i=0}^n \dbinom{n}{i} = 2^n \]

• 广义二项式定理：对于任意实数 \(x, y, n\)，有

\[(x+y)^n = \sum_{i=0}^{\infty}\dbinom{n}{i}x^iy^{n-i} \]

注意到如果 \(n > a > 0\)，则必定有 \(a^{\underline{n}} = 0\) 即 \(\tbinom{a}{n} = 0\)。故不难理解在真正把 \(n > 0\) 代入后二项式定理展开后，有很多为 \(0\) 的项，最后得到的多项式都是有限的。

这个的证明在学了 泰勒级数 后是相当显然的。

• 下降幂的二项式定理：对于任意实数 \(a, b\) 和非负整数 \(n\)，有

  \[(a+b)^{\underline{n}} = \sum_{i=0}^n\dbinom{n}{i}a^{\underline{i}}b^{\underline{n-i}} \]

可使用数学归纳法求证。

---

范德蒙德卷积

• 范德蒙德卷积恒等式：

\[\sum_{i=0}^a \dbinom{n}{i} \dbinom{m}{a-i} = \dbinom{n+m}{a} \]

组合意义：左边代表 \(n\) 中和 \(m\) 中一共选出 \(a\) 个；右边代表直接在 \(n+m\) 中选出 \(a\) 个。

生成函数：令 \(f(x)[x^m]\) 表示 \(f(x)\) 中 \(x^n\) 的系数，则等式左侧为 \((x+1)^n(x+1)^m[x^a]\)，右侧为 \((x+1)^{n+m}[x^a]\)。

• 上指标范德蒙德卷积恒等式：

\[\sum_{i=a}^{n-b} \dbinom{i}{a} \dbinom{n-i}{b} = \dbinom{n+1}{a+b+1} \]

组合意义：右边表示在 \(n+1\) 个东西中选出 \(a+b+1\) 个；左边表示枚举第 \(a+1\) 个东西。

生成函数：等式右侧为 \((-x+1)^{a+b+2}[x^{n-a-b}]\)，等式左侧为 \((-x+1)^{a+1}(-x+1)^{b+1}[x^{n-b-a}]\)。（至于这个构造到底是怎么想到的，可能得等学了生成函数再回头看了。）

---

Lucas 定理

\[\dbinom{n}{m} \equiv \dbinom{n \bmod p}{m \bmod p} * \dbinom{\lfloor\frac{n}{p}\rfloor}{\lfloor\frac{m}{p}\rfloor} \pmod{p} \]

什么时候使用 Lucas 定理？\(p\) 为质数且 \(n, m \ge p\) 时。

• P3807 【模板】卢卡斯定理/Lucas 定理

• P4345 [SHOI2015] 超能粒子炮·改：Lucas 定理常常结合数位 DP 或递归解决。

---

隔板法

把一个有 \(n\) 个不相同物品的序列分成可以为 \(0\) 的 \(m\) 段，方案数为：

\[\dbinom{n+m-1}{m-1} \]

如果隔板法的每个间隔有下界（下界可以不同，但是第几个间隔的下界是多少必须固定），可以先把下界总数从 \(n\) 中减去。

P5520 [yLOI2019] 青原樱：可将树看作隔板。

---

环排列

\(n\) 的长度，\(m\) 种颜色。可以旋转，不能翻转。

\[\dfrac{m^n}{n} \]

---

多重集排列数

\[\dfrac{(a_1+a_2+\dots+a_n)!}{a_1!a_2!\dots a_n!} \]

---

错位排列

排列上每个位置的数和其下标的值都不一样。

\(D_n\) 表示长度为 \(n\) 的错位排列数量，则有：

\[D_n = (n-1)(D_{n-1}+D_{n-2}) \]

思路主要是将数值 \(n\) 先接到一个长度为 \(n-1\) 的序列后，然后通过把最后一项与前 \(n-1\) 个项中的一项交换得到错位排序。

P4921 [MtOI2018] 情侣？给我烧了！（头好晕，回头来看。）

---

卡特兰数

\(C_n\) 表示长度为 \(2n\) 的合法括号序列数量。

递推式（枚举第一个括号对内部括号数量）：

\[C_n = \sum_{i=0}^{n-1} C_i C_{n-1-i} \]

组合数：

\[C_n = \dfrac{1}{n+1}\dbinom{2n}{n} \]

---

第二类斯特林数

\(\begin{Bmatrix}n\\m\end{Bmatrix}\) 为将 \(n\) 个不同元素划分成 \(m\) 个无标号非空集合的方案数。

\(O(n^2)\) 递推：

\[\begin{Bmatrix}n\\m\end{Bmatrix} = m\begin{Bmatrix}n-1\\m\end{Bmatrix} + \begin{Bmatrix}n-1\\m-1\end{Bmatrix} \]

普通幂转下降幂：

\[m^n = \sum_{i=0}^n \begin{Bmatrix}n\\i\end{Bmatrix} m^{\underline{i}} \]

组合意义：左侧为用 \(m\) 种颜色给 \(n\) 个物品上色；右侧为将 \(n\) 个物品分为若干组，每个组涂同一种颜色。

• 例一：

  \[\sum_{i=0}^n i^k \]

  其中 \(n \le 10^9, k \le 5000\)。

  使用第二类斯特林数将普通幂转为下降幂，再将下降幂转为组合数，使用上指标求和。

• 例二：P6620 [省选联考 2020 A 卷] 组合数问题

  这道题推式子有两点巧妙。一是通过调换 \(\sum\) 顺序把下降幂与多项式系数分离，二是最后二项式定理容易瞪不出来。

---

鸽巢原理

把 \(n\) 个球放入 \(k\) 个盒子中，则至少一个盒子里有 \(\ge\lceil\frac{n}{k}\rceil\) 个球，至少有一个盒子里有 \(\le\lfloor\frac{n}{k}\rfloor\)。

• Kuroni and Impossible Calculation：这道题等价于将 \(n\) 个球放入 \(m\) 个盒子内。如果有 \(n \ge m\)，则必定存在一个盒子内有超过两个球，答案则必等于 0。其余情况即 \(n < m\) 暴力即可。

---

Prufer 序列

一个值域为 \([1, n]\)，长度为 \(n-2\) 的序列。它与一棵 \(n\) 个节点的有标号树互为双射。

由树构造 Prufer 序列：每次选标号最小的叶子节点，删去，并记录它所相连的节点。直到只剩两个节点。可以用堆维护。

由 Prufer 序列构造树：每个点的度数为在 Prufer 序列中出现次数 \(+1\)，因此可以维护当前标号最小的叶子节点。

结论：\(n\) 个点的不同有标号生成树数量：

\[n^{n-2} \]

一些树的组合计数问题可以转化为 Prufer 序列的组合计数问题求解。

• 例一：

  

  

---

Burnside 定理

置换群学习笔记

P4128 [SHOI2006] 有色图

---

基本容斥

“当我们需要计算不满足条件 \(A\) 的方案数时，有时会选择正难则反，用总方案数减去满足条件 \(A\) 的方案数来得到答案。”

显然 \(S\) 是 \(2^n\) 级别的。因此，使用容斥原理时的 \(n\) 一般来说都比较小，或者说可以通过组合数合并某些情况。

• P1450 [HAOI2008] 硬币购物：限制是每种硬币的个数，用硬币使用没有任何限制的方案数用容斥减去有硬币超过的。

• 再谈错排：限制是值和下标不相等。

• Another Filling the Grid：部分直接使用限制条件，其余限制使用容斥。

• 求 \(n\) 个点的有标号 DAG 个数，其中 \(n \le 5000\)：并没有听懂。

• P5664 [CSP-S2019] Emiya 家今天的饭：此题的引入部分用到一点容斥，即计算每种菜品超过一半的方案数，而又因为只可能同时有一种菜品超过一半，计算并不为 \(2^n\) 级别。真正巧妙之处在 DP 方程剔除无关状态。

---

\(\min-\max\) 容斥

（感觉上面的证明有点问题，应该只有在 \(a_i\) 互不相等的情况下才能这么推吧？）

如果我们要通过 \(\min\) 求 \(\max\)，也一样有：

\[\max_{i \in S}a_i = \sum_{T \in S, T \ne \emptyset}(-1)^{|T|+1}\min_{i \in T}a_i \]

• P5643 [PKUWC2018] 随机游走：这道题的用 \(\min-\max\) 容斥转为正常期望 dp 后，时间复杂度为 \(O(2^nnq)\)。如果想要让时间复杂度更低，需要使用高维前缀和（在 这篇博客 中阐释得还清楚，它尤其在求二进制子集的和时使用）。

• Become Big For Me

---

二项式反演

主要用于 \(f(x)\) 和 \(g(x)\) 之间的互化。题目一般要求 \(g(x)\)，而 \(f(x)\) 是一个人为构造的、比较好求的函数。

更具体地说，二项式反演的题目中 \(g(x)\) 一般是“恰好”的方案数，\(f(x)\) 一般是构造为“钦定”某组元素必选、然后求方案数。二者之间满足的反演关系证明如下（这是以下面集合计数一题为例的，下文的 \(\text{intersect}(C)\) 表示 \(C\) 方案中交集的大小）：

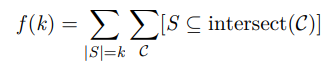
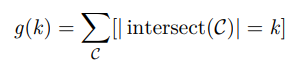
• 集合计数：我觉得一大难点在看出来所谓 \(f(k)\)，即“钦定了 \(k\) 个元素在交集里的方案数”是很好求的（这是一个任选若干集合的问题）；另一大是在推导 \(f(x)\) 和 \(g(x)\) 的关系时。

• P4859 已经没有什么好害怕的了：这个和上一道题是一样的构造方法。

• Stranger Trees

• 扩展 \(\min-\max\) 容斥：通过二项式反演给每个 \(\max\) 添上系数，扩展到第 \(k\) 小的 \(\min-\max\) 容斥。

  

---

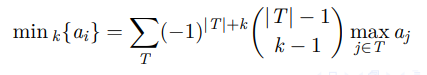
普通生成函数（OGF）

生成函数是一个很美妙的东西。它在代数与组合数学之间建立了联系，并且将一些复杂的组合问题巧妙地化为了代数问题。

这是生成函数的一种，被称为 OGF（普通生成函数）。

根据定义可以发现，序列相加则对应生成函数相加，序列做数乘则对应生成函数做数乘。换句话说，如果我们定义一个以序列为参数、以其生成函数为返回值的函数，那么该函数将会是一个线性函数。然而，生成函数相乘将遵循多项式乘法的规则，这时生成函数相乘就不等同于序列对应项相乘了。

当该多项式存在无穷项时，我们也可以称其为形式幂级数环。虽说是无穷项，但其实很多的形式幂级数环都可以通过相减法、微积分等方法化为封闭形式。很美妙不是么——看上去无穷的函数其实可以那么简洁地表示出来。

• 例一：等比数列

  等比数列的形式幂级数环为：\(f(x)=\sum_{i=0}^{\infty}c^ix^i\)，而 \(cxf(x)=\sum_{i=1}^{\infty}c^ix^i\)，二者相减得到 \((cx-1)f(x) = 1\)，故而 \(f(x) = \frac{1}{cx-1}\)。

  
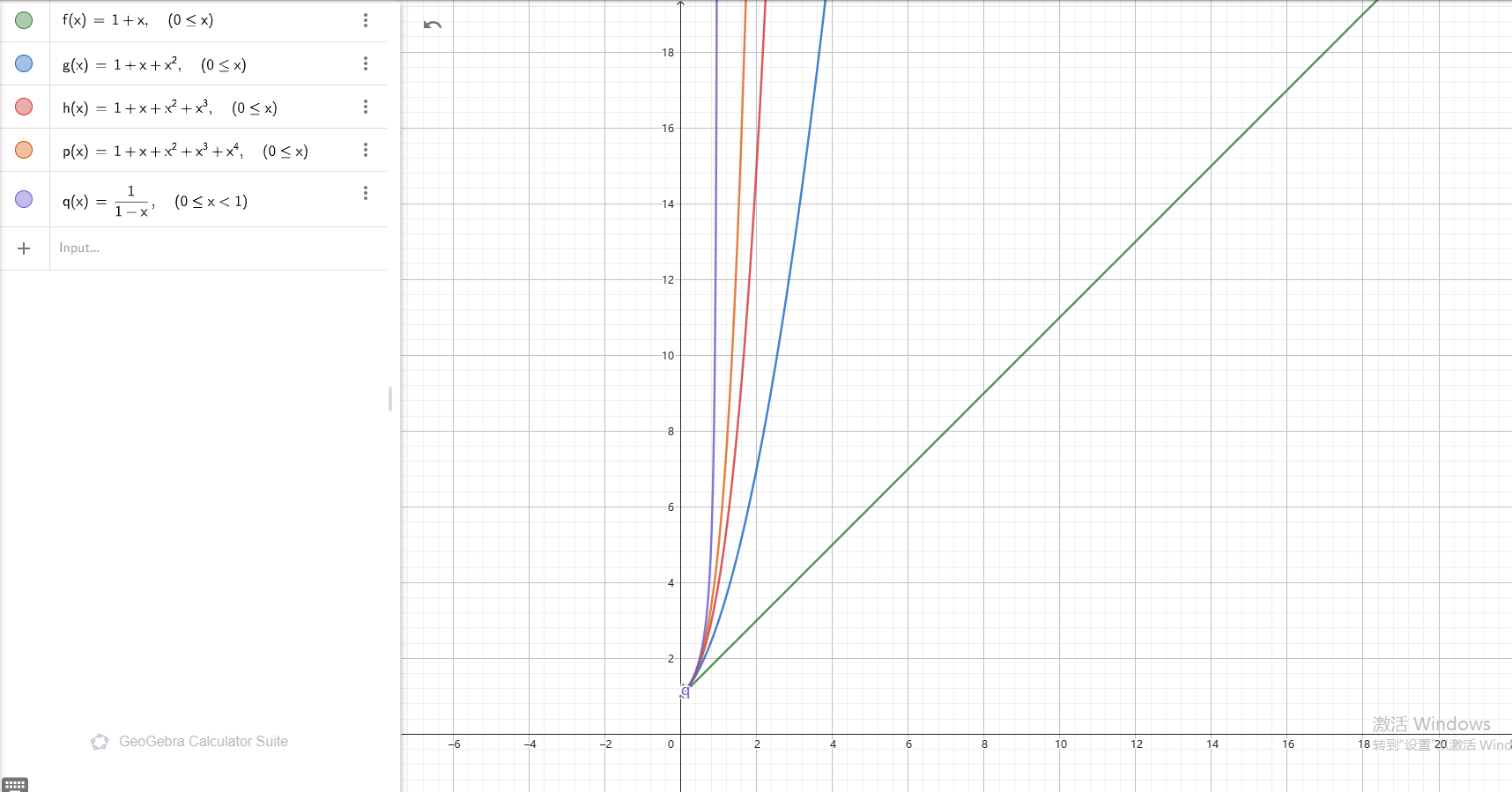
  （图例：数列 \(1, 1, 1, \dots\) 的生成函数和它的封闭形式）

• 例二：斐波那契数列

  斐波那契数列的形式幂级数环为：\(F(x)=\sum_{i=0}^{\infty}f_ix^i\)。在等式 \(f_i=f_{i-1}+f_{i-2}\) 两侧乘上 \(x^i\)、并对该方程求和，则有 \(\sum_{i=2}^{\infty}f_ix^i = \sum_{i=2}^{\infty}f_{i-1}x^i + \sum_{i=2}^{\infty}f_{i-2}x^i\)，等同于 \(F(x)-x = xF(x)+x^2F(x)\)，于是可得：\(F(x) = \frac{x}{-x^2-x+1}\)。

• 例三：差为 \(1\) 的等差数列

  该数列的形式幂级数环为：\(f(x)=\sum_{i=0}^{\infty}ix^i\)。在等式 \(a_i=a_{i-1}+1\) 两侧乘上 \(x^i\)，并……（后面和斐波那契的做法是一样的）……最终得到 \(f(x)=\frac{-x^2+x+1}{x^2-2x+1}\)。

以下是一些常见数列（形式幂级数）的封闭形式：

（其中后三个的证明都需要用到 泰勒展开 或广义二项式定理）

那么把一个形式幂级数环大费周章化为封闭形式有什么用呢？举个例子，在一个题目中，你想要求一些形式幂级数环的卷积的通项公式。你就可以先求得这些形式幂级数环的封闭形式，然后用它们的封闭形式相乘，得到它们卷积的封闭形式。接着，你就可以将这个卷积的封闭形式拆分为若干较为简单的函数之和。由于你知道这些简单函数所对应的形式幂级数环是什么，你就可以得到这个卷积的形式幂级数环，也就得到了卷积对应序列通项公式。卡特兰数的通项公式就是这么得到的。

生成函数的一大用处是刻画组合问题。一般来说，我们把一些个数限制刻画为函数中 \(x\) 的上标，方案数刻画为 \(x\) 的系数，然后通过多项式相乘来实现在每组内选一个，并且答案为某一项的系数。

• 例一：

  

  

• 例二：

  （背包问题）：有 \(n\) 种物品，第 \(i\) 种物品有 \(c_i\) 个，每个代价为 \(w_i\) 元。求花了 \(m\) 元的方案数。

  这个的生成函数应该是 \(\prod_{i=1}^n\sum_{j=0}^{c_i}x^{jw_i}\)，答案为 \([x^m]\)。

  与前一个问题不同的地方在于，背包问题是一种中仅能选一个，所以我们选择将同一种物品的不同次幂归在一个括号内；而前一个问题则是若干种都能选任意次，因此将每个种归在一个括号内，求同一个括号的次幂即可。

---

指数生成函数（EGF）

指数生成函数又称 EGF。与前面提到的 OGF 是相对的。

《具体数学》是这么解释引入 EGF 的原因的：当原数列 \(a_i\) 的 OGF 相当复杂，而 \(\frac{a_i}{i!}\) 的 EGF 相当简单时，我们将更情愿研究它的 EGF。

• \(a_i = c^i\)：这个对 \(x\) 进行一个换元为 \(cx\)，再根据 \(b_i = \frac{1}{i!}\) 的封闭形式为 \(e^x\)，就可以相当容易地证得。

• \(a_i = c^{\underline{i}}\)：它的 EGF 显然为一个二项式定理的展开形式。

• \(a_i = [i \bmod 2 = 0]\)：因为生成函数的加法等同于对应序列的加法，这里可以看作将 \(i \bmod 2 = 1\) 的项减去了。

EGF 主要用于刻画若干种数的排列问题。详见排列组合一题。

• 排列组合

  

  

  这道题揭示了用 EGF 刻画的本质：将组合数进行拆解，即可将 OGF 转化为 EGF。答案则通过乘上 \(n!\) 将 EGF 还原为 OGF。

• 例二：

  

  列出绿色、红色、蓝色的 EGF，将这三个 EGF 相乘，得到答案的 EGF，即可得到答案的通项公式。

• 再谈二项式反演：

  

---

多项式 exp / 多项式 ln

• 多项式 exp

  

  “良定义”即能在有限的求和内求出每一项的值，尽管原本的式子是个无限求和。

  为什么一定要在 \(F(x)[x^0] = 0\) 的条件下呢？当 \(F(x)[x^0] = 0\) 时，最低的次项为 \(x^1\)；此时如果你想要拼凑出次数为 \(n\) 的项，在每一次都选 \(x^1\) 的情况下，你最多仅能选 \(n\) 次，即有效的 \(i < n\)；反之，当 \(i \ge n\) 时，就绝对拼凑不出 \(x^n\) 项。而当 \(F(x)[x^0] \ne 0\) 时，由于能够选到 \(x^0\)，\(i \ge n\) 也就可以拼凑出 \(x^n\)，这个运算也就不良定义了。

• 多项式 ln

  

  至于怎么证明 \(\ln(x+1)\) 的形式幂级数环是这个，需要用到 微积分。

说来这两个东西本身有什么用呢？我们可以考虑 \(\frac{F(x)^i}{i!}\) 的组合意义：在若干组物品中，每组有 \(f_i\) 个，在可以重复选一个物品的情况下选出 \(i\) 个的方案数。则 \(e^{F(x)}\) 的组合意义为：在若干组物品中，每组有 \(f_i\) 个，在可以重复选一个物品的情况下，选出任意个的方案数。

组合意义是钉死了的。所以这么看来多项式 exp / 多项式 ln 的应用范围是比较狭窄的。

• P4841 [集训队作业2013] 城市规划：令 \(f_n\) 表示 \(n\) 个点的简单有标号无向连通图的数目，\(g_n\) 表示 \(n\) 个点的简单有标号无向图的数目。由上面的推导，容易证明：\(G = e^F\)，于是直接用多项式 \(\ln\) 计算 \(F\) 即可。

• 多项式 exp / 多项式 ln 的 \(O(n \log n)\) 计算方法：见 多项式乘法（FFT）学习笔记

---

点值表示与下降幂表示

用人话阐释一遍这个定理：对于一个多项式，它的点值表示的 EGF，与它的下降幂表示的生成函数，满足一个类似前面二项式反演的关系。

这玩意儿只能说是相当的怪异。但它提供了一种在点值表示和下降幂表示之间互化的思路。

• Similar Polynomials

  首先如果我们已经有了这两个多项式的系数，我们就可以通过二项式定理得到某一个 \(x_i\) 的系数的方程，很容易求解 \(s\)。

  然后因为下降幂也有二项式定理，我们只需要套前面的式子，求出下降幂表示就行了。