多项式乘法（FFT）学习笔记

Reference:

@自为风月马前卒 亦 @attack 的博客

@一扶苏一 的博客

@FlashHu 的博客

---

---

一、什么是 FFT

快速傅里叶变换（Fast Fourier Transform）是一种用于在 $O(n\log n)$ 实现多项式“点值表示法”和“系数表示法”之间变换的算法。

而往往在把系数表示法转化为了点值表示法后，我们可以更方便地解决一些问题，比如说多项式乘法。

---

---

二、思想

以 P3803 【模板】多项式乘法（FFT） 为例。

---

1. 多项式相乘

其实很简单，这里给出一个形式化定义。

设 $f(x)$ 的系数为向量 $(a_0,a_1,\dots ,a_{n-1})$，$g(x)$ 的系数为 $(b_0,b_1,\dots ,b_{m-1})$，则 $f(x)\ast g(x)$ （亦称 $f(x),g(x)$ 的卷积）的系数 $(c_0,c_1,\dots ,c_{n+m-1})$ 满足：

$$c_j=\sum _{i=0}^j{a}_i\ast b_{j-i}$$

---

2. 点值表示法

如果要在 $O(n^2)$ 的时间内解决这道题该怎么办？很简单，根据“多项式相乘的形式化表述”中的那个式子递推即可。

为了优化复杂度，前人们引入了多项式的一个新的表示法——点值表示法。具体地，每一个多项式可以看成一个函数，那么每一个取值 $x$ 都可以对应一个点 $(x,f(x))$。明显，对于一个 $n-1$ 次的多项式，当我们取 $n$ 个不同点时，即可唯一地确定一个多项式。

引入点值表示法对于复杂度的优化有什么益处呢？如果现在已经有了两个多项式的点值表示法，且每个点取的 $x$ 是相同的，那么它们的卷积的点值表示法即为 $(x,f(x)\ast g(x))$。这一计算可以在 $O(n+m)$ 的时间内完成。(当然，由于相乘后多项式次数增高，对于 $f(x),g(x)$ 分别计算点值表示法时，不能只各取 $n,m$ 个点，都要至少取到 $n+m$ 个才可以直接相乘计算它们的卷积。)

但是由于直接计算点值表示法的复杂度仍旧为 $O(n^2)$ 的，这看上去对复杂度并没有起到任何的优化效果。于是让我们请出神奇的快速傅里叶变换，看它是如何在 $O(n\log n)$ 的时间内实现系数表示法和点值表示法之间的转换的。

---

3. 一点点前置数学知识

• 三角函数

• 向量

• 复数

（前两者由于笔者在攥稿时已经在数学课上学习过了，暂且略去。）

• 虚数单位：定义常数 $i$ 满足 $i^2=-1$，称为虚数单位。

• 复数：定义形如 $a+bi(a,b\in \mathbf{R})$ 的数为复数。

• 实数和虚数：当且仅当 $b=0$ 时，它是实数；当且仅当 $b\ne 0$ 时，它是虚数；当且仅当 $a=0$ 且 $b\ne 0$ 时，它是纯虚数。

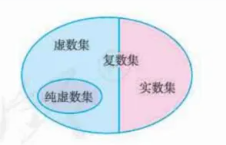
• 复平面：我们已知实数与数轴上的数一一对应。由于一个复数可以唯一地写作 $a+bi(a,b\in \mathbf{R})$，所以每一个复数都可以对应平面上的一个向量——$(a,b)$。称这个平面为复平面。$x$ 轴是实数轴，即实轴；$y$ 轴为纯虚数轴，即虚轴。

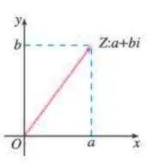
• 模（绝对值）：定义复数所对应向量的模，为该复数的模（又称绝对值）。形式化地，可表示为 $\sqrt{a^2+b^2}$。

• 幅角：以 $x$ 轴正半轴为始边，复数对应的向量所在的射线为终边，形成的角。

• 三角表示法：一个复数还可以用模长 + 幅角的形式表示。设模长为 $r$，幅角为 $\theta$，则它的三角表示法为：$r(\cos \theta +i\sin \theta )$。

• 复数的加、减：和向量的加减法则是一样的。

• 复数的乘法：

  • 代数上来说，设 $x=a+bi,y=c+di$，则有：

    $$\begin{array}{rl}x\times y& =(a+bi)(c+di)\\ & =ac+bci+adi+bd{i}^2\\ & =ac+bci+adi-bd\\ & =(ac-bd)+(bc+ad)i\end{array}$$

  • 几何上来说，它是模长相乘、幅角相加。设复数 $x=r_1(\cos {\theta }_1+i\sin {\theta }_1),y=r_2(\cos {\theta }_2+i\sin {\theta }_2)$，则有：

    $$\begin{array}{rl}x\times y& =r_1{r}_2(\cos {\theta }_1+i\sin {\theta }_1)(\cos {\theta }_2+i\sin {\theta }_2)\\ & =r_1{r}_2(\cos {\theta }_1\cos {\theta }_2+i\cos {\theta }_1\sin {\theta }_2+i\sin {\theta }_1\cos {\theta }_2+i^2\sin {\theta }_1\sin {\theta }_2)\\ & =r_1{r}_2[(\cos {\theta }_1\cos {\theta }_2-\sin {\theta }_1\sin {\theta }_2)+i(\cos {\theta }_1\sin {\theta }_2+\sin {\theta }_1\cos {\theta }_2)]\\ & =r_1{r}_2[\cos ({\theta }_1+{\theta }_2)+i\sin ({\theta }_1+{\theta }_2)]\end{array}$$

• 单位根：定义满足 $x^n=1$ 的 $x$ 为 $n$ 次单位根。注意，同次的单位根不止一个。这里姑且将所有 $n$ 次单位根的集合记作 $E_n$。

• 本原单位根：定义 $x\in E_n$，满足 $E_n\subseteq \{y|y=x^k,k\in \mathbf{N}\}$（说人话，就是它的非负整数次幂可以生成所有的别的 $n$ 次单位根），为 $n$ 次本原单位根。记作 ${\omega }_n$。

• 本原单位根的几何意义：在复平面上作一个单位圆。从 $x$ 轴开始，把单位圆 $n$ 等分，圆上分出来的点中幅角最小的那一个就是 ${\omega }_n$。其余的点，则都可以写作 ${\omega }_n^k$（$k$ 为 $0\sim n-1$ 的整数），这一结论由于复数乘法的几何意义是显然的。

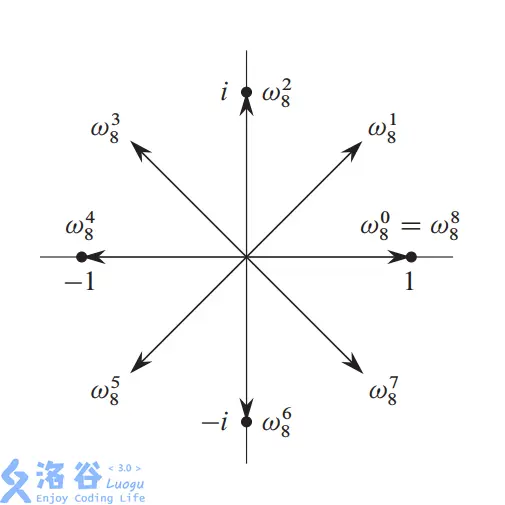
（引自 @FlashHu 的博客）

• ${\omega }_n^k$ 的值：根据复数乘法的几何意义，明显可以得到：

$${\omega }_n^k=\cos {\displaystyle \frac{k\ast 2\pi }{n}}+i\sin {\displaystyle \frac{k\ast 2\pi }{n}}$$

【注意下面两条性质，它们是快速傅里叶变换的关键。】

• 性质一：${\omega }_{an}^{ak}={\omega }_n^k$

  证明：${\omega }_{an}^{ak}=\cos \frac{ak\ast 2\pi }{an}+i\sin \frac{ak\ast 2\pi }{an}={\omega }_n^k$

• 性质二：${\omega }_n^{k+\frac{n}{2}}=-{\omega }_n^k$

  证明：${\omega }_n^{k+\frac{n}{2}}={\omega }_n^k\ast {\omega }_n^{\frac{n}{2}}={\omega }_n^k\ast {\omega }_2^1=-{\omega }_n^k$

---

4. 快速傅里叶变换（FFT）

简单概括一下 FFT 的思想：将所有的 ${\omega }_n^k$（$k$ 为 $0\sim n-1$ 的整数）代入多项式，并且利用上面的两条性质，进行分治优化。

【注意：以下推导默认 $n$ 为偶数】

先设当前有一个多项式：

$$f(x)=a_0+a_{1}x+a_2{x}^2+\cdots +a_{n-1}{x}^{n-1}$$

对它的下标进行奇偶性分类：

$$f(x)=(a_0+a_2{x}^2+\cdots +a_{n-2}{x}^{n-2})+(a_{1}x+a_3{x}^3+\cdots +a_{n-1}{x}^{n-1})$$

给右边的式子提个公因数，将左右化得更为相似：

$$f(x)=(a_0+a_2{x}^2+\cdots +a_{n-2}{x}^{n-2})+x(a_1+a_3{x}^2+\cdots +a_{n-1}{x}^{n-2})$$

设：

$$f_1(x)=a_0+a_{2}x+\cdots +a_{n-2}{x}^{\frac{n}{2}-1}$$

$$f_2(x)=a_1+a_{3}x+\cdots +a_{n-1}{x}^{\frac{n}{2}-1}$$

则：

$$f(x)=f_1(x^2)+x{f}_2(x^2)$$

这样，每次计算 $f(x)$ 时，我们就可以递归分别计算两个项数更少的 $f_1(x)$ 和 $f_2(x)$，再加起来得到答案了。

看上去还是没用？让我们尝试随便代入一个值 ${\omega }_n^k(k<\frac{n}{2})$：

$$\begin{array}{rl}f({\omega }_n^k)& =f_1({\omega }_n^{2k})+{\omega }_n^k{f}_2({\omega }_n^{2k})\\ & =f_1({\omega }_{\frac{n}{2}}^k)+{\omega }_n^k{f}_2({\omega }_{\frac{n}{2}}^k)\end{array}$$

再代入一个值 ${\omega }_n^{k+\frac{n}{2}}(k<\frac{n}{2})$：

$$\begin{array}{rl}f({\omega }_n^{k+\frac{n}{2}})& =f_1({\omega }_{\frac{n}{2}}^{k+\frac{n}{2}})+{\omega }_n^{k+\frac{n}{2}}{f}_2({\omega }_{\frac{n}{2}}^{k+\frac{n}{2}})\\ & =f_1({\omega }_{\frac{n}{2}}^k)-{\omega }_n^k{f}_2({\omega }_{\frac{n}{2}}^k)\end{array}$$

可以发现，前一个式子和后一个式子几乎是一样的。因此，当我们用递归计算 $f_1$、$f_2$ 的方法计算出 $f({\omega }_n^k)$ 时，我们完全可以顺便求出 $f({\omega }_n^{k+\frac{n}{2}})$。如此，计算范围就缩小了一半。

而在递归分别计算 $f_1$ 和 $f_2$ 的过程中，也同样可以按照上面的方法，缩小一半范围计算。

当然，运用上述方法的必要条件是项数为偶数。为了保证每一层递归时项数都是偶数，我们要将项数设置为一个大于等于原项数的 $2$ 正整数次幂，并补上一些系数为 $0$ 的项。

一直递归，层数最多为 $\log n$。总复杂度 $O(n\log n)$。

---

5. 快速傅里叶逆变换（IFFT）

快速傅里叶变换让我们成功地将系数表示法转化为了点值表示法。但是在我们运用点值表示法快速地得到了新多项式时，还需要把点值表示法转化回系数表示法。这时就需要用到快速傅里叶逆变换。

快速傅里叶逆变换的思路非常奇怪。它的思路是：将当前得到的点值表示，当作一个多项式的系数，再对这个新多项式做一遍快速傅里叶变换求点值表示。可以证明，这个二次快速傅里叶变换所得到的的结果和原本的系数表示法之间存在某种关系。

这里为了帮助我自己理解，手推（抄）了一遍 dalao@自为风月马前卒 给出的快速傅里叶逆变换的证明。

$(y_0,y_1,\dots ,y_{n-1})$ 为多项式 $(a_0,a_1,\dots ,a_{n-1})$ 在 $x$ 取 $({\omega }_n^0,{\omega }_n^1,\dots ,{\omega }_n^{n-1})$ 时的点值表示（亦称傅里叶变换）。形式化地，它满足：

$$y_i=\sum _{j=0}^{n-1}{a}_j({\omega }_n^i{)}^j$$

设有一向量 $(c_0,c_1,\dots ,c_{n-1})$ 为 $(y_0,y_1,\dots ,y_{n-1})$ 在 $x$ 取 $({\omega }_n^0,{\omega }_n^{-1},\dots ,{\omega }_n^{-(n-1)})$ 时的点值表示。形式化地，它满足：

$$c_k=\sum _{i=0}^{n-1}{y}_i({\omega }_n^{-k}{)}^i$$

然后开始推导。

$$\begin{array}{rl}{c}_k& =\sum _{i=0}^{n-1}{y}_i({\omega }_n^{-k}{)}^i\\ & =\sum _{i=0}^{n-1}(\sum _{j=0}^{n-1}{a}_j({\omega }_n^i{)}^j)({\omega }_n^{-k}{)}^i\\ & =\sum _{i=0}^{n-1}\sum _{j=0}^{n-1}{a}_j({\omega }_n^i{)}^j({\omega }_n^{-k}{)}^i\\ & =\sum _{i=0}^{n-1}\sum _{j=0}^{n-1}{a}_j({\omega }_n^{j-k}{)}^i\\ & =\sum _{j=0}^{n-1}{a}_j(\sum _{i=0}^{n-1}({\omega }_n^{j-k}{)}^i)\end{array}$$

观察上式中第二个 $\sum$ 的内容，它是一个关于 ${\omega }_n^{j-k}$ 的等比数列。当 $j-k\ne 0$ 时，根据等比数列求和公式，有：

$$\begin{array}{rl}\sum _{i=0}^{n-1}({\omega }_n^{j-k}{)}^i& ={\displaystyle \frac{({\omega }_n^{j-k}{)}^n-1}{{\omega }_n^{j-k}-1}}\\ & ={\displaystyle \frac{({\omega }_n^n{)}^{j-k}-1}{{\omega }_n^{j-k}-1}}\\ & ={\displaystyle \frac{1-1}{{\omega }_n^{j-k}-1}}\\ & =0\end{array}$$

而当 $j-k=0$ 时，有 ${\omega }_n^{j-k}=1$，那么求和的结果即为 $n$。

因此有：

$$c_k=a_{k}n$$

即：

$$a_k={\displaystyle \frac{c_k}{n}}$$

在学了 skc 的网课后，发现这还有另外一种从矩阵角度的理解方法：

---

---

三、实现

1. 递归版

我们来浅浅总结一下整体的流程：

• 先求出一个 $N$，满足为第一个大于 $n+m$ 的 $2$ 的正整数次幂，令它为新项数。并为两个多项式补上一些系数为 $0$ 的项。

• 对多项式 $f(x),g(x)$ 分别跑一次 FFT，得到二者的点值表示法。

• 将二者的点值表示法逐个相乘，得到二者卷积的点值表示法。

• 对卷积的点值表示法跑一遍 IFFT，得到它的系数表示法。

FFT 的流程：

• 当前递归到的是一个项数为 $n$ 的多项式。

• 将该多项式的系数按照奇偶性拆为两个多项式，分别递归计算值。

• 通过计算到的两个多项式的答案，合并得到当前的答案。

IFFT 的流程：

• 将原本的单位根 ${\omega }_n$ 改为 ${\omega }_n^{-1}$，对点值表示法计算二次 FFT。一般直接使用性质 ${\omega }_n^{-k}={\omega }_n^{-k}\ast {\omega }_n^n={\omega }_n^{n-k}$ 来计算 ${\omega }_n^{-k}$。

• 将二次 FFT 后得到的值全都除以 $n$，即得到系数表示法。

直接使用递归法由于 FFT 的常数过大，在洛谷上无法通过。

---

2. 递推版

回忆一下上文的递归式：

$$f({\omega }_n^k)=f_1({\omega }_{\frac{n}{2}}^k)+{\omega }_n^k{f}_2({\omega }_{\frac{n}{2}}^k)$$

$$f({\omega }_n^{k+\frac{n}{2}})=f_1({\omega }_{\frac{n}{2}}^k)-{\omega }_n^k{f}_2({\omega }_{\frac{n}{2}}^k)$$

如果按照递归写法，它需要开很多数组 $f,f1,f2,\dots$，而接下来介绍的递推法能够在只开一个数组的情况下解决问题。

观察下图：

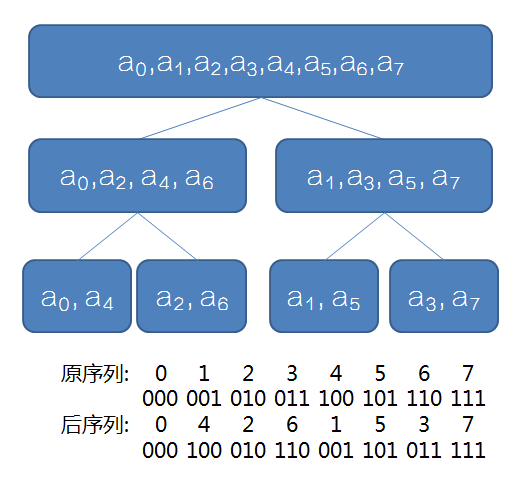
可以发现两条巧妙的性质：

1. 对于当前规模为 $n$ 的递归层，$f[k]$ 和 $f[k+\frac{n}{2}]$ 两个位置在下一层递归中恰好对应 $f_1[k]$ 和 $f_2[k]$。

2. 最后结束时的序列为原序列的二进制翻转。

性质 1. 使得我们每一次从下往上递推时只需要调用下面的 $f[k],f[k+\frac{n}{2}]$ 即可计算出 $f[k],f[k+\frac{n}{2}]$。这样就只需要开一个数组了。

性质 2. 使得我们可以轻松地得到递推的起始状态。

---

3. c++ STL complex 类

实现的时候我们可以选择自己封装一个复数类，也可以选择使用 c++ STL 自带的 complex 类。

1. 定义

基本格式为 complex<T> x;，T 为一种浮点数类型。

初始化变量的值有很多种方式。下面列举了几种：

complex<double> a(3, 4);
complex<double> b = 3.0 + 4i;
complex<double> c = {3, 4};
complex<double> d(3);//只初始化实部

2. 实部和虚部

使用 real(x), imag(x) 可以分别取出 x 的实部和虚部，但无法赋值。

使用 x.real(), x.imag() 也可以分别取出 x 的实部和虚部。并且，可以通过 x.real(a), x.imag(b) 的方式分别将 x 的实部和虚部赋值为 a 和 b。

3. 运算

complex 类内置了复数加减乘除，以及与实数的加减乘除运算。我们只需要用运算符号正常运算即可。

4. 输出

complex 类内置了输入输出流。直接写 cout<<x<<endl;，会输出形如 (real,imag) 的结果。

---

4. code

点击查看代码

#include<bits/stdc++.h>
#define cp complex<double>
using namespace std;

const int MAXN = (1<<21)+5;
const double Pi = acos(-1);//为确保精度，需要写成这样。 
int n, m, N = 1, rev[MAXN];
cp f[MAXN], g[MAXN], h[MAXN];

inline void Prework(){//预处理二进制翻转。 
    while(N <= n+m)   N <<= 1;
    for(int i = log2(N)-1, t = 0; i >= 0; i--){
        int x = t;
        for(int j = 0; j <= x; j++) rev[++t] = (1<<i)|rev[j];
    }
    return;
}

inline void DFT(cp a[], int v){//v 表示当前是 w_n^k 还是 w_n^{-k} 
    for(int i = 0; i < N; i++)   if(rev[i] < i) swap(a[rev[i]], a[i]);
    for(int i = 2; i <= N; i <<= 1)//枚举当前层中，每一组的大小 i 
        for(int k = 0; k < i/2; k++){//枚举组内编号 k
			//从逻辑上应该先枚举 j 再枚举 k，但是我为了只计算一次不同的 w_n^k，就调换了一下顺序。 
            cp w(cos(2*Pi/i*k), sin(2*Pi/i*k*v));
            for(int j = 0; j < N; j += i){//枚举每个组的开头下标 j 
                cp x = a[j+k], y = a[i/2+j+k];
                a[j+k] = x+w*y;
                a[i/2+j+k] = x-w*y;
            }
        }
    return;
}

inline void IDFT(cp a[]){
    DFT(a, -1);
    for(int i = 0; i < N; i++)  a[i] /= N;
    return;
}

int main(){
    scanf("%d%d", &n, &m);
    for(int i = 0; i <= n; i++){
        int x; scanf("%d", &x);
        f[i].real(x);
    }
    for(int i = 0; i <= m; i++){
        int x; scanf("%d", &x);
        g[i].real(x);
    }
    Prework();
    DFT(f, 1), DFT(g, 1);
    for(int i = 0; i < N; i++)  h[i] = f[i]*g[i];
    IDFT(h);
    for(int i = 0; i <= n+m; i++)   printf("%d ", int(round(real(h[i]))));

    return 0;
}

---

---

四、NTT

NTT 和 FTT 不同的地方在于，它被用于解决模意义下的多项式乘法。

其实本质上的思路和 FFT 只能说是一模一样。只不过 NTT 中的“单位根”，是模意义下的单位根而已。

如何求出模意义下的单位根呢？首先需要看一下 原根与阶。设在该模数 $p$ 下有原根 $g$，可以证明，任意满足 $x\equiv g^t(\mathrm{mod}p)$ 的 $x$，一定满足 $t\text{ord}(x)=\text{ord}(g)$。故存在一个单位根 ${\omega }_n\equiv g^{\frac{\text{ord}(g)}{n}}=g^{\frac{\phi (p)}{n}}$（当然，前提条件一定是 $n|\phi (p)$）。

NTT 的题目一般用 $p=998244353$ 做模数，因为它是一个质数，所以有 $\phi (p)=p-1$，且满足 $p-1=2^{23}\times 7\times 17$，所以在 $n\le 2^{23}$ 的情况下都存在 $n$ 次单位根。而这个模数的最小原根为 $3$，可以直接用。

点击查看代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;

const int MAXN = (1<<21)+5;
const ll Mod = 998244353, Rt = 3;
int n, m, N = 1, rev[MAXN];
ll f[MAXN], g[MAXN], h[MAXN];

inline ll Quick_Power(ll x, ll p){
    if(!p)  return 1;
    ll tmp = Quick_Power(x, p>>1);
    if(p&1) return tmp*tmp%Mod*x%Mod;
    else    return tmp*tmp%Mod;
}

inline ll Inv(ll x){
    return Quick_Power(x, Mod-2);
}

inline void Prework(){
    while(N <= n+m)   N <<= 1;
    for(int i = log2(N)-1, t = 0; i >= 0; i--){
        int x = t;
        for(int j = 0; j <= x; j++) rev[++t] = (1<<i)|rev[j];
    }
    return;
}

inline void DFT(ll a[], ll v){
    for(int i = 0; i < N; i++)   if(rev[i] < i) swap(a[rev[i]], a[i]);
    for(int i = 2; i <= N; i <<= 1)
        for(int k = 0; k < i/2; k++){
            ll w = Quick_Power(Rt, (Mod-1)/i*(i+k*v));
            for(int j = 0; j < N; j += i){
                ll x = a[j+k], y = a[i/2+j+k];
                a[j+k] = (x+w*y)%Mod;
                a[i/2+j+k] = (x-w*y%Mod+Mod)%Mod;
            }
        }
    return;
}

inline void IDFT(ll a[]){
    DFT(a, -1);
    ll inv = Inv(N);
    for(int i = 0; i < N; i++)  (a[i] *= inv) %= Mod;
    return;
}

int main(){
    scanf("%d%d", &n, &m);
    for(int i = 0; i <= n; i++) scanf("%lld", f+i);
    for(int i = 0; i <= m; i++) scanf("%lld", g+i);
    Prework();
    DFT(f, 1), DFT(g, 1);
    for(int i = 0; i < N; i++)  h[i] = f[i]*g[i]%Mod;
    IDFT(h);
    for(int i = 0; i <= n+m; i++)   printf("%lld ", h[i]);

    return 0;
}

---

---

五、应用

【FBI Warning：以下的应用全都在模 $x^n$ 意义下进行，也就是说我们只考虑多项式的 $0\sim x^n$ 项。】

1. 多项式求逆

P4238 【模板】多项式乘法逆

参照 @Great_Influence 的题解，写得超级清楚。

【关于他的推导过程，这里留一点备注：为什么平方以后模数就可以由 $x^{\lceil \frac{n}{2}\rceil }$ 变为 $x^n$？因为 $B^{\prime }-B$ 的前 $\lceil \frac{n}{2}\rceil -1$ 项为 $0$，故 $(B^{\prime }-B{)}^2$ 的最高非 $0$ 次项 $\ge x^n$。】

这个方法简言之，就是构造了一个 $\lceil \frac{n}{2}\rceil$ 到 $n$ 的递推式。通过主定理，可以计算得总复杂度为 $O(n\log n)$（尽管单次多项式乘法也为 $O(n\log n)$）。

简记一下结论：

$$B(x)\equiv 2B^{\prime }(x)-A(x)\ast B^{\prime }(x{)}^2(\mathrm{mod}{x}^n)$$

关于实现，需要注意的是：这种结果对于 $x^n$ 取模的多项式乘法，两个因式在相乘前必须对 $x^n$ 取模，且也必须完整地按照普通 NTT 的过程算出 $2n$ 个项后再对 $x^n$ 取模。

点击查看代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;

const int MAXN = (1<<19)+5;
const ll Mod = 998244353, Rt = 3;
int n, Rev[MAXN];
ll W, w[MAXN];

inline ll Quick_Power(ll x, int p){
	if(!p)	return 1;
	ll tmp = Quick_Power(x, p>>1);
	if(p&1)	return tmp*tmp%Mod*x%Mod;
	else	return tmp*tmp%Mod;
}

inline ll Inv(ll x){
	return Quick_Power(x, Mod-2);
}

struct Polynomial{
	int len;
	ll a[MAXN];
	
	inline void Input(){
		for(int i = 0; i < n; i++)	scanf("%lld", a+i);
		len = 1;
		while(len < n)	len <<= 1;
		return;
	}
	
	inline void Output(){
		for(int i = 0; i < n; i++)	printf("%lld ", a[i]);
		return;
	}
	
	inline void Module(int N){
		for(int i = N; i < len; i++)	a[i] = 0;
		len = N;
		return;
	}
	
	inline void DFT(int N){
		w[0] = 1;
		for(int i = 1; i < N; i++)	w[i] = w[i-1]*W%Mod;
		for(int i = 0; i < N; i++)	if(Rev[i] > i) swap(a[i], a[Rev[i]]);
		for(int i = 2; i <= N; i <<= 1)
			for(int j = 0; j < N; j += i)
				for(int k = 0; k < i/2; k++){
					ll x = a[j+k], y = a[i/2+j+k];
					a[j+k] = (x+y*w[N/i*k]%Mod)%Mod;
					a[i/2+j+k] = (x-y*w[N/i*k]%Mod+Mod)%Mod;
				}
		return;
	}
	
	inline void IDFT(int N){
		W = Inv(W);
		DFT(N);
		ll inv = Inv(N);
		for(int i = 0; i < N; i++)	a[i] = a[i]*inv%Mod;
		return;
	}
	
	Polynomial operator * (const int &tmp)const{
		Polynomial ans; ans.len = len;
		for(int i = 0; i < len; i++)	ans.a[i] = a[i]*tmp%Mod;
		return ans;
	}
	
	Polynomial operator - (const Polynomial &tmp)const{
		Polynomial ans; ans.len = len;
		for(int i = 0; i < len; i++)	ans.a[i] = (a[i]-tmp.a[i]+Mod)%Mod;
		return ans;
	}
} f;

inline void Prework(int N){
    W = Quick_Power(Rt, (Mod-1)/N);
	for(int i = N>>1, j = 0; i; i >>= 1){
		int t = j;
		for(int k = 0; k <= t; k++)	Rev[++j] = Rev[k]+i;
	}
	return;
}

Polynomial operator * (const Polynomial &x, const Polynomial &y){
	int N = y.len<<1;//乘法必须算到 N*2 项 
	Prework(N);
	Polynomial X = x, Y = y, ans;
	X.Module(N>>1), Y.Module(N>>1);//对多项式项数取模 
	X.DFT(N), Y.DFT(N);
	for(int i = 0; i < N; i++)	ans.a[i] = X.a[i]*Y.a[i]%Mod;
	ans.IDFT(N);
	ans.Module(N>>1);
	return ans;
}

inline Polynomial Inv_P(Polynomial &A){
	Polynomial B = (Polynomial){1, {Inv(A.a[0])}};
	for(int N = 2; N < n*2; N <<= 1){//N 为当前取模的长度 
		B.len = N;
		B = B*2-A*B*B;
	}
	return B;
}

int main(){
	scanf("%d", &n);
	f.Input();
	Polynomial ans = Inv_P(f);
	ans.Output();
	
	return 0;
}

---

2. 多项式 ln

P4725 【模板】多项式对数函数（多项式 ln）

对 $B(x)\equiv \ln A(x)(\mathrm{mod}{x}^n)$ 求导得：

$$B^{\prime }(x)\equiv {\displaystyle \frac{A^{\prime }(x)}{A(x)}}(\mathrm{mod}{x}^n)$$

先求逆再乘法即可。

---

3. 牛顿法

这个的前置知识：微积分学习笔记。

其实前面多项式求逆的方法本质运用的是一个方法——“牛顿法”。具体可以参考 @Miskcoo 的博客。

在这里就简述一下结论。

在已知 $G(x)$ 的情况下，牛顿法被用于求出下式的 $F(x)$：

$$G(F(x))\equiv 0(\mathrm{mod}{x}^n)$$

令 $F_0(x)$ 满足：

$$G(F_0(x))\equiv 0(\mathrm{mod}{x}^{\lceil \frac{n}{2}\rceil })$$

则通过将 $G(F(x))$ 在 $F_0(x)$ 处做泰勒展开，有：

$$F(x)\equiv F_0(x)-{\displaystyle \frac{G(F_0(x))}{G^{\prime }(F_0(x))}}(\mathrm{mod}{x}^n)$$

注意这里 $F_0(x)$ 在计算前一定要保证 $x^{\lceil \frac{n}{2}\rceil }$ 以上的项一定为 0。（问我为什么？只能说从最终表达式看来是这样的，但我也不道啊。。。）

以多项式求逆举例。定义 $G(B(x))$ 满足：

$$G(B(x))\equiv {\displaystyle \frac{1}{B(x)}}-A(x)$$

则有：

$$B(x)\equiv B_0(x)-{\displaystyle \frac{\frac{1}{B_0(x)}-A(x)}{-\frac{1}{B_0(x{)}^2}}}\equiv 2B_0(x)-A(x)B_0(x{)}^2$$

这里的多项式 $A(x)$ 可以当作一个“常数项”，因为我们把多项式本身当作自变量了。

---

4. 多项式 exp

P4726 【模板】多项式指数函数（多项式 exp）

运用牛顿法推导一下就可以得到：

$$B(x)\equiv B_0(x)(1-\ln B_0(x)+A(x))(\mathrm{mod}{x}^n)$$