网络流学习笔记

FBI Warning：本文全部抄自 OIwiki、蓝书、或其他博客，毫无自己的思考，没有什么学习价值。

零、基本概念

直接走 OIwiki 或者看蓝书吧。

一、最大流

1. Ford-Fulkerson 增广

“该方法运用贪心的思想，通过寻找增广路来更新并求解最大流。”

主要流程就是每次选一些增广路，以来更新最大流。但这个贪心思路不一定能保证正确性。Ford-Fulkerson 增广的核心技术是通过设置 反向边 来实现 反悔贪心。

反向边的特性：流量与正向边互为相反数，且始终不大于零。

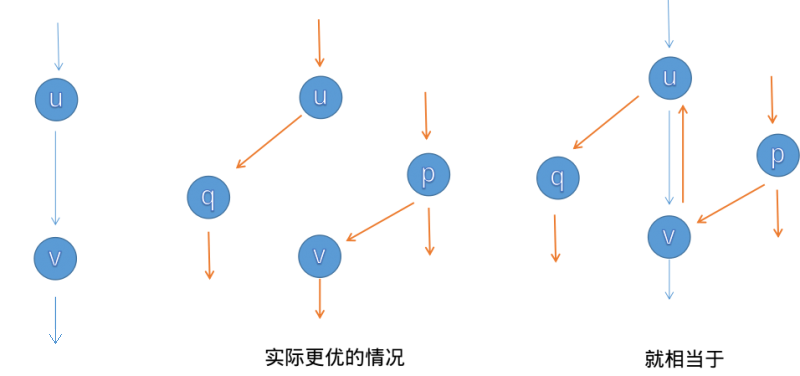
以下的 Edmonds-Karp、Dinic 和 ISAP 都是基于 Ford-Fulkerson 增广的算法。

2. Edmonds-Karp

基本流程：每次用 Bfs 选择边数最少的一条增广路，如此反复，直到没有增广路。

时间复杂度：可以证明，增广总轮数的上界为 \(O(nm)\)，单次 Bfs 的时间复杂度为 \(O(m)\)，因此总复杂度为 \(O(nm^2)\)。

点击查看代码 
#include<bits/stdc++.h>
#define ll long long
using namespace std;

const int MAXN = 205, MAXM = 5005;
int n, m, s, t, head[MAXN], pre[MAXN];
ll f[MAXN], maxflow;
bool vst[MAXN];

struct node{
	int to, nxt;
	ll wi;
} edge[MAXM*2];

inline void Add_edge(int i, int from, int to, int wi){
	edge[i].to = to;
	edge[i].wi = wi;
	edge[i].nxt = head[from];
	head[from] = i;
	return;
}

inline bool Bfs(){
	memset(vst, false, sizeof(vst));
	memset(f, 0x3f3f, sizeof(f));//f：到当前节点为止，增广路上的最小边 
	queue<int> que; que.push(s); vst[s] = true;
	while(!que.empty()){
		int cur = que.front(); que.pop();
		for(int i = head[cur]; i; i = edge[i].nxt){
			if(!edge[i].wi)			continue;
			int to = edge[i].to;
			if(vst[to])				continue;
			f[to] = min(f[cur], edge[i].wi); 
			pre[to] = i;
			vst[to] = true;
			que.push(to);
			if(to == t)	return true;
		}
	}
	return false;
}

inline void Update(){
	for(int x = pre[t]; x; x = pre[edge[x^1].to])
		edge[x].wi -= f[t], edge[x^1].wi += f[t];
	maxflow += f[t];
	return;
}

int main(){
	scanf("%d%d%d%d", &n, &m, &s, &t);
	for(int i = 1; i <= m; i++){
		int ui, vi, wi;				scanf("%d%d%d", &ui, &vi, &wi);
		Add_edge(i*2, ui, vi, wi);	Add_edge(i*2+1, vi, ui, 0);
	}
	while(Bfs())	Update();
	cout<<maxflow;
	
	return 0;
}

3. Dinic 算法

基本思想：注意到每次 EK 算法都在试着找一条边数最少的增广路。那么假如说现在有一个图，它到 \(t\) 的每一条路径的边数都是最少，可以证明这时 EK 的复杂度仅有 \(O(nm)\)。

基本流程：增广直到不存在增广路。每次增广时，先使用 Bfs 在残量网络上求出一个“分层图”（就是一个 DAG，满足每条边仅指向 Bfs 的下一层，满足上面所说的每条路径等长最小），然后用 EK 求分层图最大流，顺便就可以更新剩余容量。

优化：

  • 后继完全增广完毕的点不访问。【常数优化】

  • 当前弧优化：去掉已经增广过了的出边（代码中的 now 数组）。【复杂度优化】

  • Dfs 代替 EK 找分层图最大流：由于分层图的特殊性，这里使用 Dfs 可以得到一个常数更小、复杂度也一样的算法。

点击查看代码 
#include<bits/stdc++.h>
#define ll long long
using namespace std;

const int MAXN = 205, MAXM = 5005;
const ll INF = 0x3f3f3f3f3f3f3f3f;
int n, m, s, t, head[MAXN], now[MAXN], d[MAXN];
//d：用于记录 bfs 层数，以建立分层图

struct node{
	int to, nxt;
	ll wi;
} edge[MAXM<<1];

inline void Add_edge(int i, int from, int to, int wi){
	edge[i].to = to;
	edge[i].wi = wi;
	edge[i].nxt = head[from];
	head[from] = i;
	return;
}

inline bool Bfs(){
	memset(d, 0, sizeof(d));
	for(int i = 1; i <= n; i++)	now[i] = head[i];
	queue<int> que; que.push(s); d[s] = 1;//注意给 d[s] 赋初值，以免下方 BFS 卡死
	while(!que.empty()){
		int cur = que.front(); que.pop();
		for(int i = head[cur]; i; i = edge[i].nxt){
			if(!edge[i].wi)	continue;
			int to = edge[i].to;
			if(d[to])		continue;
			d[to] = d[cur]+1;
			que.push(to);
			if(to == t)		return true;
		}
	}
	return false;
}

inline ll Dinic(int x, ll flow){
	if(x == t)	return flow;
	ll rest = flow;
	for(int i = now[x]; i and rest; i = edge[i].nxt){//注意要保持 rest > 0
		if(!edge[i].wi)		continue;
		int to = edge[i].to;
		if(d[to] != d[x]+1)	continue;
		now[x] = i;//当前弧优化（请格外注意这里，老版蓝书上的写法有误！）
		ll tmp = Dinic(to, min(rest, edge[i].wi));
		if(!tmp)			d[to] = 0;//去掉接下来没有可增广的点
		rest -= tmp;
		edge[i].wi -= tmp;
		edge[i^1].wi += tmp;
	}
	return flow-rest;
}

int main(){
	scanf("%d%d%d%d", &n, &m, &s, &t);
	for(int i = 1; i <= m; i++){
		int ui, vi, wi;				scanf("%d%d%d", &ui, &vi, &wi);
		Add_edge(i*2, ui, vi, wi);	Add_edge(i*2+1, vi, ui, 0);
	}
	ll maxflow = 0;
	while(Bfs())	maxflow += Dinic(s, INF);
	cout<<maxflow;
	
	return 0;
}

时间复杂度：

  • 一般情况：可证明单轮增广复杂度为 \(O(nm)\)，一次 Bfs 复杂度为 \(O(m)\)，增广总轮数不超过 \(O(n)\)，总复杂度为 \(O(n(nm+m))\)，在稠密图中表现优异。

  • 单位容量网络（边权都为 0/1）：\(O(m \min (m^{\frac{1}{2}}, n^{\frac{2}{3}}))\)。

  • 单位容量网络 + 除了源、汇点外出入度都为 1（即求 二分图最大匹配 时的网络）：\(O(m\sqrt{n})\)。

4. ISAP 算法

reference：钱逸凡 的博客、OIwiki

基本思想：ISAP 可看作对 Dinic 的常数优化。在 Dinic 中，每次求完分层图的最大流时，都需要 Bfs 一次。而 ISAP 的思想就是：每次增广时实时更新分层图，就只需要在开头进行一次 Bfs 即可。

基本流程：

  • 进行第一次 Bfs，在反向图上，处理一个以 t 为起点的 d 数组。（因为）

  • 执行 Dfs，直到 d[s] > n：

    • 前面与 Dinic 一模一样。

    • 如果当前节点 x 被完全增广了（即流入量还有剩余），那么尝试更新 d[x]：

      访问 x 的每一条出边，求它后继的 d 数组最小值，并将 d[x] 设置为最小值加一。

      • 如果找不到任何一个后继，将 d[x] 设置为 n+1。

      • 否则更新 d[x]，重置当前弧优化数组 now[x]。

点击查看代码 
inline void Bfs(){
	queue<int> que; que.push(t); d[t] = 1;
	for(int i = 1; i <= n; i++)	now[i] = head[i];
	while(!que.empty()){
		int cur = que.front(); que.pop();
		for(int i = head[cur]; i; i = edge[i].nxt){
			int to = edge[i].to;
			if(d[to])	continue;
			d[to] = d[cur]+1;
			que.push(to);
		}
	}
	return;
}

inline void Update(int x){
	int nd = n+1;
	for(int i = head[x]; i; i = edge[i].nxt)
		if(edge[i].ci)	nd = min(nd, d[edge[i].to]+1);
	d[x] = nd;
	now[x] = head[x];
	return;
}

inline ll ISAP(int x, ll flow){
	if(x == t)	return flow;
	ll rest = flow;
	bool flag = false;
	for(int i = now[x]; i and rest; i = edge[i].nxt){
		if(!edge[i].ci)		continue;
		int to = edge[i].to;
		if(d[to]+1 != d[x]) continue;
		now[x] = i;
		ll k = ISAP(to, min(rest, edge[i].ci));
		edge[i].ci -= k;
		edge[i^1].ci += k;
		rest -= k;
	}
	if(rest)	Update(x);
	return flow-rest;
}

还有另一种写法，可以减少码量：在 update 函数中，只需要将 d[x]++ 即可。

这个时候就有人（比如我）要问了：为什么可以这样？按照原本来说，d[x] 不一定只增加 1 啊？

但若 d[x] 在此处的增加不合法的话，下一次迭代到 x，它会再次 +1，一直迭代直到合法为止。

这个时候又有人要问了：那这样常数好大啊！

但原本 update 函数的常数就很大啊：要访问 x 的每一条出边。因此不分伯仲罢了。

除了当前弧优化外，ISAP 还有一种优化：GAP 优化。记录每一种 d 数组的每一个值的数量 gap[d[x]]。当更新 d 时出现一个 gap[d[x]] 变成 0，那么说明出现了 “断层”，可以推断出增广已经结束。

inline void Update(int x){
	if(--gap[d[x]] == 0)	{END = true; return;}
	++gap[++d[x]];
	now[x] = head[x];
	return;
}

5. 例题

二、最小割

1. 定义 & 定理

一种点的划分方式（或者说边集）：将所有的点划分为 \(S, T\) 两部分，其中源点 \(s \in S, t \in T\)。

割的容量：所有从 \(S\) 连接到 \(T\) 的边的容量之和。

最小割：求得一个割使得该割容量最小。或者说，在一个网络中删去一些边使得该图 \(s, t\) 不连通，并使这些边的容量之和最小。

最大流最小割定理：最大流 = 最小割。感性地反证一下，最小割如果小于最大流，则删去最小割后仍存在增广路，那么最小割并没使图不连通，所以最小割大于等于最大流，相等时最大流取最大、最小割取最小。【详细证明：here，我会回来看的。】

构造最小割：在求完最大流之后，在剩下的残量网络中，源点能到达的点 与 不能到达的点 之间的所有边。（明显，这些边的和即为最大流。）

2. 例题

  • 有线电视网：网络流建模的 边点互换 和 INF 防割断 技巧。点转边：拆为入点 + 出点，边转点：加一个点即可。还有求多源点多汇点最小割技巧：枚举源点汇点即可。

三、费用流

1. 概念

网络上每条边不但有容量限制 \(c\)，还有一个单位流量的费用 \(w\)。当该边的流量为 \(f\) 时，该边的费用就为 \(f \times w\)。

该网络中总费用最小的最大流称为 最小费用最大流，同理还有最大费用最大流，合称费用流。

注意，费用流一定是建立在最大流的基础上的。

2. 算法

费用流的主流算法为 SSP 算法，一般来说就已经够用了。【详见：关于网络流费用流算法复杂度】

SSP 仍旧是基于 Ford-Fulkerson 增广求最大流的，反边容量设置为 0、费用设置为相反数。只不过在寻找增广路时，它并不是像 EK、Dinic 那样选择边数最少的那一条，而是选择费用最少的一条。正确性是显然的。

所以，实现时只要把 EK 或 Dinic 的 Bfs 部分换成 SPFA 就可以了。（因为有反向边有负边权，就不能用 dijkstra。（关于为什么不会产生负环：【？？？我不道啊】））

由于失去了 Bfs 的复杂度保证，这里的复杂度只能做到 FF 增广任选路径时的复杂度：设最终求出最大流的值为 \(f\)，那么增广轮数最差为 \(O(f)\)，单次增广最差为 \(O(mn)\)，总复杂度为 \(O(nmf)\)。（这种关于值域的多项式复杂度被称为 伪多项式复杂度。）

具体实现建议直接以原本 EK 为框架，不用写 Dinic 了。因为反正都失去了 Bfs 的复杂度保证，EK、Dinic 实现的 SSP 版本实际复杂度没有什么区别。

P3381 【模板】最小费用最大流

点击查看代码 
#include<bits/stdc++.h>
#define ll long long
using namespace std;

const int MAXN = 5005, MAXM = 5e4+5;
int n, m, s, t, head[MAXN], pre[MAXN];
bool inq[MAXN];
ll w[MAXN], c[MAXN], maxflow, mincost;

struct node{
	int to, nxt;
	ll ci, wi;
} edge[MAXM<<1];

inline void Add_edge(int i, int from, int to, int ci, int wi){
	edge[i] = (node){to, head[from], ci, wi}, head[from] = i;
	return;
}

inline bool SPFA(){
	memset(c, 0x3f3f, sizeof(c));
	memset(w, 0x3f3f, sizeof(w));
	queue<int> que; que.push(s);
	w[s] = 0, pre[t] = 0;//inq[s] 可以不标，pre[t] 用于判断有无解 
	while(!que.empty()){
		int cur = que.front(); que.pop();
		inq[cur] = false;
		for(int i = head[cur]; i; i = edge[i].nxt){
			int to = edge[i].to;
			//怎么求出一条路径的最小费用？怎么找到一条最小费用路？
			//直接相加费用就可以了
			//因为增长流量在路上每一处都是相等的，满足分配律
			if(!edge[i].ci or w[to] <= w[cur]+edge[i].wi)	continue;
			w[to] = w[cur]+edge[i].wi;
			c[to] = min(c[cur], edge[i].ci);
			pre[to] = i;
//			if(to == t)		return true;不能这么写，因为 SPFA 不能直接确定最短 
			if(!inq[to])	que.push(to), inq[to] = true;
		}
	}
	return pre[t];
}

inline void Update(){
	for(int i = pre[t]; i; i = pre[edge[i^1].to]){
		edge[i].ci -= c[t], edge[i^1].ci += c[t];
		mincost += edge[i].wi*c[t];
	}
	maxflow += c[t];
	return;
}

int main(){
	scanf("%d%d%d%d", &n, &m, &s, &t);
	for(int i = 1; i <= m; i++){
		int ui, vi, ci, wi;				scanf("%d%d%d%d", &ui, &vi, &ci, &wi);
		Add_edge(i*2, ui, vi, ci, wi);	Add_edge(i*2+1, vi, ui, 0, -wi);
	}
	while(SPFA())	Update();
	cout<<maxflow<<" "<<mincost;
	
	return 0;
}

四、最小割树

1. 描述

P4897 【模板】最小割树（Gomory-Hu Tree）

给定一个无向连通图，多次查询，询问不同源点汇点间的最小割。（既然能查询最小割，那肯定也可以查询最大流。）

2. Gomory-Hu Tree 算法

这个算法使用了两种思想：分治 + 最小割。

最小割树的定义：

对于任意树边 \((u, v)\) 满足 \(w(u, v)\) 为原图中 \(u, v\) 之间的最小割，\((u, v)\) 分开的两部分点为原图中 \(u, v\) 之间的最小割分开的两部分点。

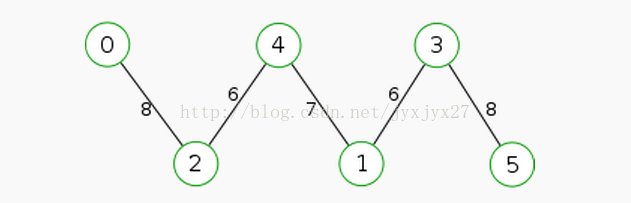
如果代码按照某种特定写法写的话，建出来的树一定是一条链。

引理：

树上任意两点 \(u, v\) 的最小割，是二者在树上路径所经过边的最小值。

posted @ 2024-02-22 11:08  David_Mercury  阅读(17)  评论(0)  编辑  收藏  举报