回文树（回文自动机）学习笔记
学习回文自动机时感觉很多资料的思路都来得很陡，而且缺失了基本的原理证明。因此在这里重新整理了一下。
用途
可以求出每一个字符的“最长后缀回文”，也可以储存所有的回文串。
思维过程
现在我们要做的是：在对一个字符串逐个插入字符时，求得它与串内其余字符形成的新回文串。
观察可以发现，如果 \(x \sim i\) 形成回文串，那么 \(x+1 \sim i-1\) 必须为回文串。
对于任意一个已经确定是回文串的 \(x+1 \sim i-1\) 进行单次匹配，只需要比较 \(s[x]\) 和 \(s[i]\) 是否相等即可。
对于新插入的节点 \(i\)，找到 \(1 \sim i\) 的后缀的最长回文，模仿 KMP 的方式，进行如下操作：先试着和 \(1 \sim i-1\) 后缀的最长回文匹配。如果已经成功匹配了那不用说；如果失败了，就试着与 \(1 \sim i-1\) 后缀的次长回文匹配，还不行就与 \(1 \sim i-1\) 后缀的次次长回文匹配，直到匹配成功或后缀已经是空串了。
那么，是不是可以像 KMP 那样，对于每一个节点 \(i\)，记录一下它后缀的最长、次长回文分别的位置，就可以快速在这些后缀间跳跃了？可以发现，这其实是不能直接实现的。最主要的问题是“次长的次长”的位置并没有在先前被计算过，更本质的原因是，它似乎并不是任何节点的最长后缀回文。
但其实我们可以证明，某个节点的“次长”，一定与先前某个节点的“最长”完全相同。
证明：
来观察一下这幅图：
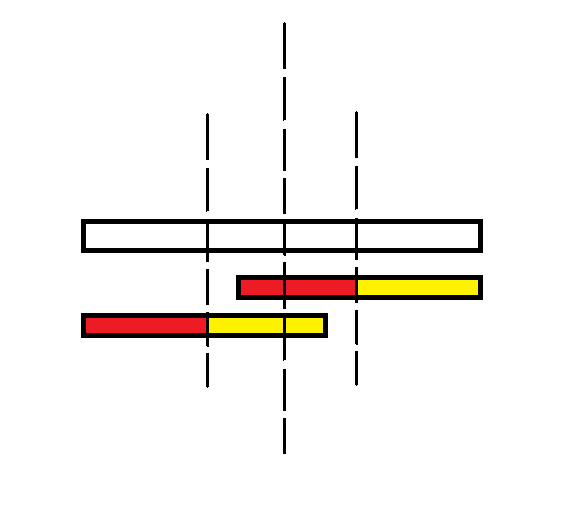
白色的矩形为 \(1 \sim i-1\) 的最长后缀回文，而右侧的红 - 黄矩形为次长的。
根据回文串的对称性，易得红 - 黄矩形的左侧有一个和它镜像对称的红 - 黄矩形；又由于回文串的镜像还是它本身，左侧的的矩形和右侧的矩形完全相同。
但是这时我们依旧不能确保左侧矩形它的右端点的“最长”。不过，如果它不是最长的话，就又回到了上图中同样的情景：原本的左侧矩形变成了现在的右侧矩形，而又绝对有一个新的左侧矩形与之完全相同。如此递归往复，总可以保证红 - 黄矩形是某个节点的“最长”。
证毕。
很显然，当两个子串完全相同时，就说明它们的最长回文后缀完全相同。也就是说，如果我们知道最开始那个完全相同的“最长”，知道它的“次长”，就可以找到当前这个“次长”的次长。如此，次长的次长、次长的次长的次长等等都可以顺利求出，便可以模仿 KMP 的“跳后缀”过程了。
那如何求出那个相等的最长回文后缀呢？引入一个数据结构——字典树。字典树显然是非常适合干这件事的：它可以快速查询一个相同的字符串，还很容易组织众多的字符串。
注意，这里节点一旦被插入到字典树中，它代表的就不是自己原本在字符串中的下标了——它代表的是一个回文串本身。
算法实现
有了刚刚的分析，算法的实现就很明了了。
-
字典树的建立
这里的字典树比较特殊。首先，我们得建两棵字典树——因为回文串有两种，长度为奇数以及长度为偶数的。
节点 0 代表偶回文树的根，一个回文串的读法为“从当前节点开始，往上读到根节点，再从上往下读回当前节点”；节点 1 代表奇回文树的根，一个回文串的读法为“从当前节点开始，往上读到根节点，与根节点相连的边只读一次，再从上往下读回来”。下图的蓝边代表的就是字典树的普通边。
-
fail 指针
fail 指针就是方才所提到的“指向次长后缀回文串”的指针，也是下图的黑边。容易发现，fail 的连接也构成了一棵树。
初始化 0 节点的 fail 指向 1，1 节点的 fail 无所谓（但如果你仔细观察了下图，会发现以 1 为父亲的节点的 fail 都是 0，这在后面的代码里会特判处理）。
-
len
len 代表回文串的长度，这是树中每个节点还需要存储的一个信息。这里有一个小技巧：将节点 1 的 len 设置为 -1，节点 0 的 len 设置为 0，这样每个节点的 len 就是其父节点的 +2。
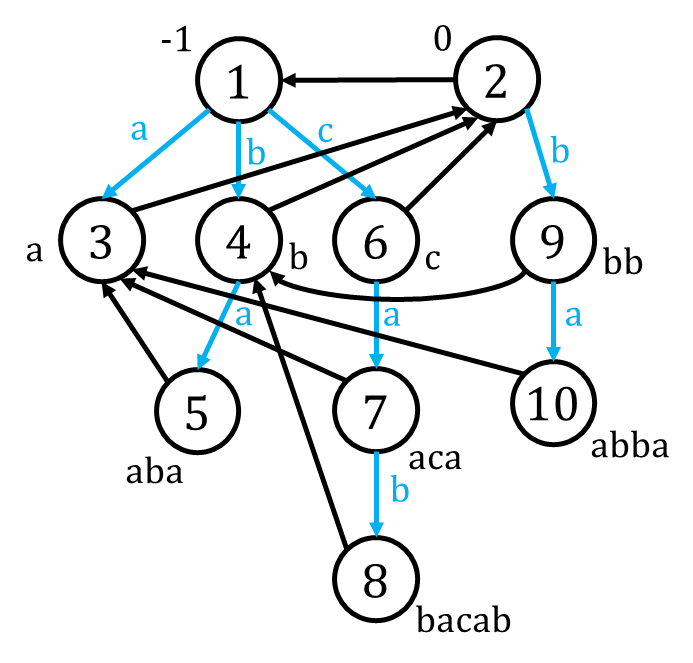
（图片引自某位人士的博客，我忘了是谁了。）
-
具体过程：把字符串中的节点逐个插入字典树。对于节点 \(i\)：
-
记录 \(i-1\) 的最长后缀回文在回文树中的对应节点 lst。从 lst 开始，不断跳 fail 指针，直到找到一个节点 \(p\)，使得 \(s[i] = s[i-len_p-1]\)。
-
新建一个节点代表 \(i\) 的最长后缀回文，接到 \(p\) 的一个儿子指针下。注意，如果 \(p\) 已经有对应的儿子了，就像正常的字典树那样，我们就不用再新建了，下面一步“找 fail” 也不用进行了。
-
找到了 \(i\) 的“最长”，接下来要求“次长”——也就是 fail 了。只需要从 \(fail_p\) 开始接着跳 fail，直到又找到一个节点 \(q\) 满足 \(s[i] = s[i-len_q-1]\)，\(q\) 就是 \(i\) 的 fail 了。
-
更新一下 lst。
-
ok，show you the code.（其实很短）
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 5e5+5;
int n, tot = 1;
char str[MAXN];
struct Trie{
int fail, len, sum, ch[26];
} tree[MAXN];
inline int Get_fail(int pt, int i){
while(str[i] != str[i-tree[pt].len-1]) pt = tree[pt].fail;
return pt;
}
int main(){
scanf("%s", str+1);
n = strlen(str+1);
tree[0] = (Trie){1, 0, 0};
tree[1] = (Trie){0, -1, 0};
for(int i = 1, lst = 0; i <= n; i++){
str[i] = (str[i]-97+tree[lst].sum)%26+97;
int p = Get_fail(lst, i);
if(!tree[p].ch[str[i]-'a']){
++tot;
//注意以下两句的顺序关系。其实这里隐含了一个特判，即以 1 为父亲的节点，它们的 fail 应指向 0。
tree[tot].fail = tree[Get_fail(tree[p].fail, i)].ch[str[i]-'a'];
tree[p].ch[str[i]-'a'] = tot;
tree[tot].sum = tree[tree[tot].fail].sum+1;
tree[tot].len = tree[p].len+2;
}
lst = tree[p].ch[str[i]-'a'];
printf("%d ", tree[lst].sum);
}
return 0;
}
复杂度证明
这个我不太清楚，大概是用势能之类的搞一下，网上肯定有很多说得清楚的资料。反正是 \(O(n)\) 的。
例题
-
Palisection：还没想出来，先咕。。。
