[POJ1852] Ants

题目

An army of ants walk on a horizontal pole of length l cm, each with a constant speed of 1 cm/s. When a walking ant reaches an end of the pole, it immediatelly falls off it. When two ants meet they turn back and start walking in opposite directions. We know the original positions of ants on the pole, unfortunately, we do not know the directions in which the ants are walking. Your task is to compute the earliest and the latest possible times needed for all ants to fall off the pole.

Input

The first line of input contains one integer giving the number of cases that follow. The data for each case start with two integer numbers: the length of the pole (in cm) and n, the number of ants residing on the pole. These two numbers are followed by n integers giving the position of each ant on the pole as the distance measured from the left end of the pole, in no particular order. All input integers are not bigger than 1000000 and they are separated by whitespace.

Output

For each case of input, output two numbers separated by a single space. The first number is the earliest possible time when all ants fall off the pole (if the directions of their walks are chosen appropriately) and the second number is the latest possible such time.

Sample Input

2

10 3

2 6 7

214 7

11 12 7 13 176 23 191

Sample Output

4 8

38 207

解说

先翻译一下题目。一根长为L的木棍上有n只蚂蚁，已知各个蚂蚁的位置，但不知道初始时各个蚂蚁的朝向。现在它们开始爬，速度一直为1，除非它们碰见别的蚂蚁，不然方向绝不会改变。如果碰见别的蚂蚁就会掉头，保持原速度换方向爬行（动   量   守   恒）。问所有蚂蚁都掉下木棍所需要的最短时间和最长时间。

这怎么办啊，没思路。模拟倒是简单，但这么多蚂蚁，每个都向左或向右，这时间效率直接指数级了，肯定不行。

换个思路，如果没有碰撞的话一切简单至极，重点就在碰撞。那么我们想象一下碰撞的情景。

 

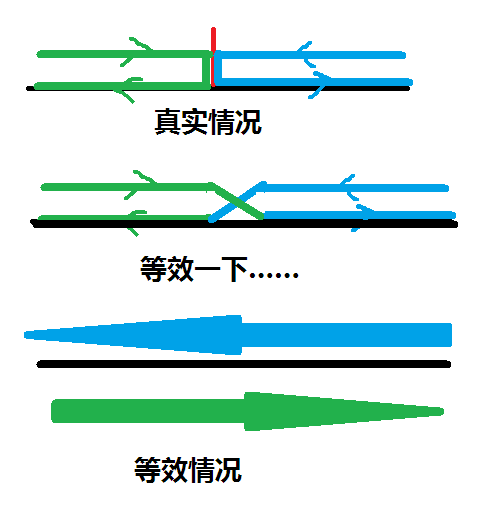
（论如何用一张画崩的图毁掉一篇博客）

由于所有蚂蚁没有任何区别，我们完全可以把碰撞的过程看做是一个互换的过程，一只蚂蚁接替了另一只蚂蚁继续走它未走完的路，这样的话这两只蚂蚁就可以看做没有发生丝毫干扰，各自继续走自己的路，正如上图所示。

既然这样，这个题就变得和上面说的没有碰撞的极其简单的情况一样了，可以秒了。

代码

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
int main(){
    int T;
    scanf("%d",&T);
    while(T--){
        int l,n;
        scanf("%d%d",&l,&n);
        int maxn=-1,minn=-1;
        for(int i=1;i<=n;i++){
            int num;
            scanf("%d",&num);
            maxn=max(maxn,max(num,l-num));
            minn=max(minn,min(num,l-num));//注意minn
                        //逻辑关系容易弄错
        }
        printf("%d %d\n",minn,maxn);
    }
    return 0;
} 

（说实话基本没必要了……）

 

幸甚至哉，歌以咏志。