[NOI2003][树的直径]逃学的小孩
题目
解说
分享题说实话最开始都没什么思路,之前的大部分基本都看了一下题解启发思路。

但这道题我可以大声而骄傲地说:它 是 我 完 完 全 全 自 己 做 出 来 的 !
当然,代价就是Vjudge上WA了5遍,洛谷上WA了1遍,坑杀了我一节半课的时间。
那么,转到正题,思路是怎么样的呢?
首先可见这个图是一棵树,我们需要找到三个点,暂时叫ABC吧。其中(A到B的距离+C到AB距离中较短的)这一值最小。
(以下maxdis代表树的直径,maxv代表第一遍DFS找到的直径端点,End代表第二遍DFS找到的另一个端点,bj i代表点是否在直径上,ans i 以及之后的ans1 i 代表节点 i 到maxv的距离,ans2 i 代表节点 i 到End的距离,b代表最后的答案)
很显然这属于树的直径题。用两遍DFS找出树的两个顶点……之后呢?我在这里第一次卡住了。
由于万恶的样例带来的错觉,我觉得题目要求的点一定是在直径上。所以我就用了第三遍DFS,找出来了所有直径上的点,在第二遍DFS的时候顺带计算出ans i,之后循环一遍找到答案就行。循环大概就是:
for(int i=1;i<=n;i++) if(bj[i]==1&&i!=End&&i!=maxv) b=max(b,min(maxdis-ans[i],ans[i]));
然后就WA了。
之后很长时间我就卡在了这个代码的框框里,因为我一直坚定地认为要求的点在直径上。卡了半天还是感谢洛谷提供的一组错误样例让我恍然大悟:
我的C为什么一定要在直径上?!
下面是洛谷给的样例:
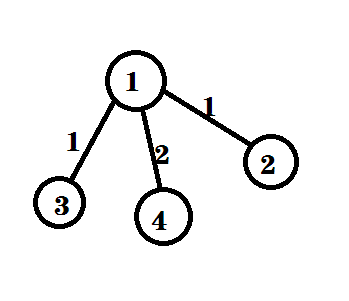
简洁明了但很有说服力。
显然,树的直径是2-4或3-4。由于这两种没有差别下面就用2-4举例。
如果按照之前的想法,C在直径上,那么我算出来的结果是4.但若我们选3作为C呢?
2到4的距离+3到2,4距离中较短的=5。
也就是说C不一定在直径上。
噫,好了,全崩了。
但是思路正确了应该就没什么问题了。我们在第二遍dfs的时候顺带算出各点到maxv的距离,之后再DFS一遍算出各点到End的距离,之后把各个点遍历一遍算min(ans1[i],ans2[i])+maxdis的最大值即可。
代码

1 #include<cstdio> 2 #include<iostream> 3 #include<queue> 4 #include<algorithm> 5 #include<cstring> 6 #include<cmath> 7 using namespace std; 8 typedef long long ll; 9 const int maxn=200000+3; 10 int n,m,tot,head[maxn],End,maxv; 11 ll maxdis,ans1[maxn],ans2[maxn]; 12 struct node{ 13 int to,next; 14 ll w; 15 }e[2*maxn]; 16 void Add(int from,int to,ll w){ 17 e[tot].w=w; 18 e[tot].to=to; 19 e[tot].next=head[from]; 20 head[from]=tot; 21 tot++; 22 } 23 void dfs1(int u,int f,ll dis){//找第一个端点 24 if(maxdis<dis) { 25 maxv=u; 26 maxdis=dis; 27 } 28 for(int i=head[u];i;i=e[i].next){ 29 int v=e[i].to;ll w=e[i].w; 30 if(v==f) continue; 31 dfs1(v,u,dis+w); 32 } 33 } 34 void dfs2(int u,int f,ll dis){//找第二个端点 35 ans1[u]=dis;//顺带求出所有点到maxv的距离 36 if(maxdis<dis) { 37 maxdis=dis; 38 End=u; 39 } 40 for(int i=head[u];i;i=e[i].next){ 41 int v=e[i].to;ll w=e[i].w; 42 if(v==f) continue; 43 dfs2(v,u,dis+w); 44 } 45 } 46 void dfs3(int u,int f,ll dis){//求所有点到End的距离 47 ans2[u]=dis; 48 for(int i=head[u];i;i=e[i].next){ 49 int v=e[i].to;ll w=e[i].w; 50 if(v==f) continue; 51 dfs3(v,u,dis+w); 52 } 53 } 54 int main(){ 55 int n,m; 56 tot=1; 57 cin>>n>>m; 58 for(int i=1;i<=m;i++){ 59 int from,to;ll w; 60 cin>>from>>to>>w; 61 Add(from,to,w); 62 Add(to,from,w); 63 } 64 dfs1(1,-1,0); 65 maxdis=0; 66 dfs2(maxv,-1,0); 67 dfs3(End,-1,0); 68 ll b=-1; 69 for(int i=1;i<=n;i++) if(i!=End&&i!=maxv) b=max(b,min(ans1[i],ans2[i])+maxdis); 70 //找最佳点 71 cout<<b; 72 return 0; 73 }
幸甚至哉,歌以咏志。


