浙江金华 图论整理
图论
- 图论
- 基础知识储备:
- 各类算法简介:
- (1)、Havel–Hakimi算法简介:
- (2)、Erdős–Gallai定理简介:
- (3)、遍历(DFS/BFS)(pass...)
- (4)、DFS Forest简介:
- (5)、欧拉回路
- (6)、最小生成树
- (7)、Matrix-Tree定理简介:
- (8)、最短路(SSSP)
- (9)、差分约束系统简介:
- (10)、Johnson算法介绍简介:
- (11)、半径/直径 (正权图)简介:
- (12)、绝对中心 && 最小直径生成树
- (13)、拓扑排序
- (14)、Hall’s marriage theorem简介:
- (15)、Kőnig's theorem简介:
- (16)、DAG最小路径覆盖简介:
- (17)、强连通分量 && 双联通分量
- (18)、割点和桥
- (19)、图论例题整理(未完...):
- Allowed Letters(CF 1009 G)代码实现:
- Revmatching (TCO 2015 1A Hard)
- Valid BFS? (CF 1037 D)
- Cycle (HDU 5215)
- 航空管制 (NOI 2010)
- ABland Yard (AGC 27 C)
- Cycling City (CF 295 E)
- Hangar Hurdles (CERC 16)
- Life of the Party (ONTAK 2010)
- Allowed Letters(CF 1009 G)
- Revmatching (TCO 2015 1A Hard)
- Bajtman i Okrągły Robin (ONTAK 2015)
- 不知名例题
- 不知名例题2
基础知识储备:
(1)、概念:
图 G 是一个二元组(V,E),其中V称为顶点集,E称为边集。它们亦可写成 V(G)和E(G)。E的元素是一个二元组数对,用(x,y)表示,其中x,y∈V。
(2)、图的储存:
①邻接表
②链式前向星
③邻接矩阵
(3)、度数序列:
①若把图 G 所有顶点的度数排成一个序列 S,则称 S 为图 G 的度数序列。
②考虑无向图,d1, d2, ... ,dn表示每个点的度数,d1 + d2 + ... + dn= 2e, 每条边被计算两次,一共有偶数个度数奇数的点。
各类算法简介:
(1)、Havel–Hakimi算法简介:
给定一串有限多个非负整数组成的序列,是否存在一个简单图使得其度数列恰为这个序列。令S=(d1,d2,...,dn)为有限多个非负整数组成的非递增序列。 S可简单图化当且仅当有穷序列S’=(d2-1,d3-1,...,d(d1+1)-1,d(d1+2),...,dn)只含有非负整数且是可简单图化的。
(2)、Erdős–Gallai定理简介:
令S=(d1,d2,...,dn)为有限多个非负整数组成的非递增序列。S可简单图化当且仅当这些数字的和为偶数,并且对任意1<=k<=n都成立。
即公式: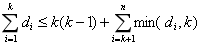
(3)、遍历(DFS/BFS)(pass...)
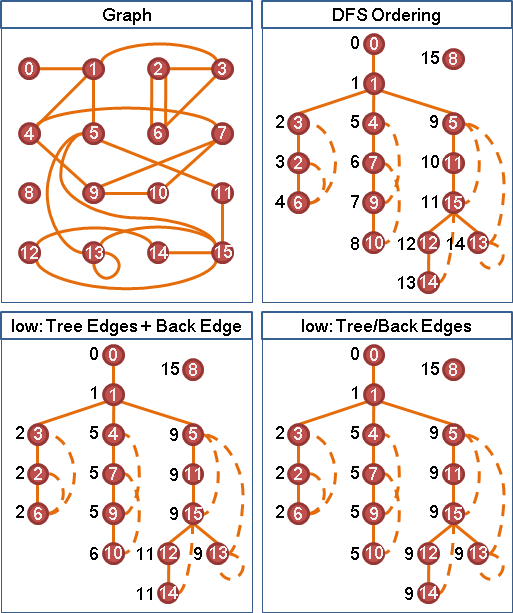
(4)、DFS Forest简介:
Tree Edge指树边
Back Edge指连向祖先的边
Forward Edge指连向子孙的边
Cross Edge指连向树其他分支的边
在无向图中只存在Tree Edge和Back
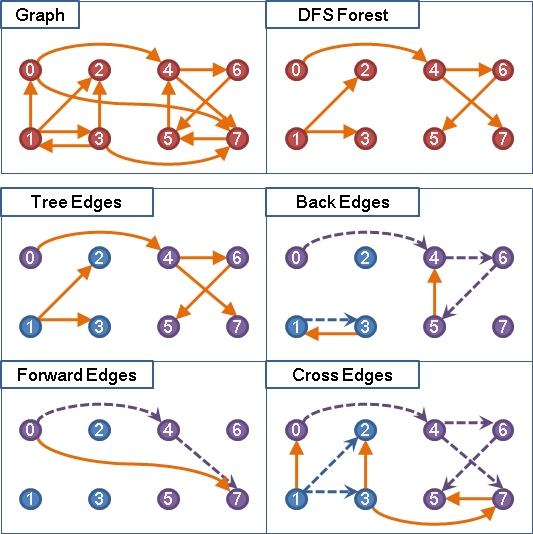
(5)、欧拉回路
①简介:
无向图有欧拉回路的充要条件为每个点度数都是偶数且边连通(注意孤立点)。有向图有欧拉回路的充要条件为每个点的 入度 = 出度 且边连通。一个联通无向图,有2k个奇数点,那么需要k条路径。
②代码实现:
inline void dfs(int u) {
for(int i=head[u];i;i=head[u]) {
while (i && vis[abs(s[i])]) i=e[i].nxt;
head[u]=i;
if(i) {
vis[abs(s[i])]=1;
dfs(v[i]);
q[++top]=s[i];
}
}
}
(6)、最小生成树
①Prim / Kruskal (复杂度: O(n^2) / O(m log m))
②Kruskal算法的正确性
拟阵(E,I)满足I的每个元素为E的子集。
空集属于I
如果A属于I,那么A的所有子集也属于I
如果A,B属于I,并且|A|>|B|,那么存在一个A中不属于B中的元素u,满足B∪{u}也属于I。
这样就被称为拟阵,对于拟阵,我们可以使用贪心算法从小到大或者从大到小选择。
令E为边集,I为所有生成森林的集合,那么(E,I)为拟阵。
常见的拟阵还有匹配拟阵和线性无关组。
③Borůvka算法简介:
一开始每个连通分量是一个点本身。每轮每个连通分量选择和其他连通分量相连的最小的边,然后合并。时间复杂度O(E log V)
④最小瓶颈生成树简介:
使得生成树树上最大边权值最小。
方法1: 最小生成树一定是最小瓶颈生成树。
方法2: 二分答案,看点是否连通。
类比找第k大值的方法,首先随机一个边权w。
然后将不超过这个边权的边加入,遍历这张图。
如果图连通,那么瓶颈不超过w,于是只需考虑边权不超过w的边。
否则将这些连通点缩起来,考虑边权大于w的边。
每次将问题的规模缩小至一半。
期望时间复杂度O(m)。
⑤生成树计数简介:
1.Prufer序列:一棵树要得到Prufer序列,方法是逐次去掉树的顶点,直到剩下两个顶点。考虑树T,其顶点为{1, 2, ... ,n}。在第i步,去掉标号最小的叶子,并把Prufer序列的第i项设为这叶的邻顶点的标号。一棵树的序列明显是唯一的,而且长为n − 2。
2.复原:设这Prufer序列长n − 2。首先写出数1至n。找出1至n中没有在序列中出现的最小数。把标号为这数的顶点和标号为序列首项的顶点连起来,并把这数从1至n中删去,序列的首项也删去。接着每一步以1至n中剩下的数和余下序列重复以上步骤。最后当序列用完,把1至n中最后剩下的两数的顶点连起来。
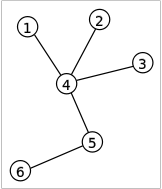
3.Cayley定理:完全图的生成树个数为n(n-2)次。如果每个点的度数为di,那么生成树个数为(n-2)!/(d1-1)!/(d2-1)!/.../(dn-1)!每个连通块大小为ai,那么添加一些边将这些连通块连通的生成树个数为a1*a2*...*an*(a1+a2+...+an)(n-2)次。
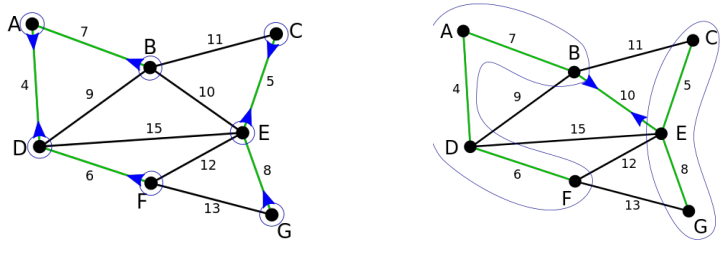
(7)、Matrix-Tree定理简介:
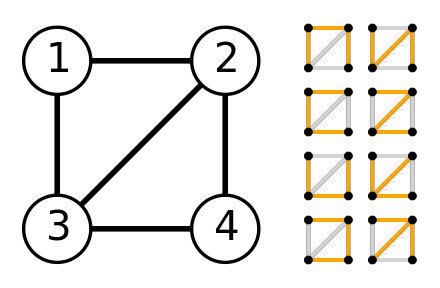
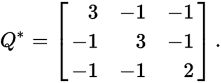
令G=D-A,然后去除G的任意一行一列G’,G’的行列式即生成树个数。有向图计数,即树形图个数。这里的D变为每个点的入度,删去第i行第i列为从第i个点出发的树形图个数。
(8)、最短路(SSSP)
①简介:
Dijkstra/Bellman Ford算法(时间复杂度O(m log n)或者O(nm))
Floyd算法(O(n^3))/ Johnson算法(负权)((nm log n))
①算法正确性:
Dijkstra 贪心
Bellman Ford 动态规划
②一些变种:
边权是0/1
双端队列,如果是0在头部插入,否则在尾部插入。
总长不超过W, 正权
使用0..W的桶+链表维护这些点,时间复杂度O(m+W)。
③最短路径树(图):
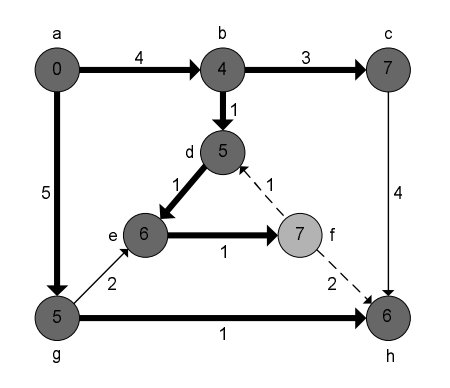
(9)、差分约束系统简介:
根据最短路有不等式dis(v)<=dis(u)+w(u,v),恰好存在一个这样的u满足条件。并且这样计算出来的dis(v)是最大的。,对于一些s(v)<=s(u)+w(u,v)的限制,可以类比最短路建图。
判断解唯一时,对原图求一遍最短路。将原图取反,边权取反,求一遍最长路。一个标号对应的是能取到的最小值,一个是最大值。如果相同则解唯一。
(10)、Johnson算法介绍简介:
首先给图中每个点一个标号h(v), 把每条边(u,v)边权改成w(u,v)+h(u)-h(v)。对于s-t的一条路径p,权值为
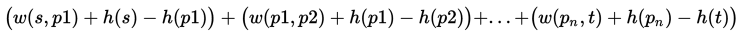
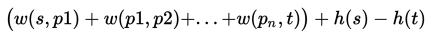
所以不会改变最短路。
从1号点出发跑一遍最短路,记h(v)=dis(v)。
由不等式可以得到dis(u)+w(u,v)>=dis(v),也就是改完之后边权非负。
之后可以每个点用Dijkstra跑。
(11)、半径/直径 (正权图)简介:
u的偏心距:ecc(u)=max dis(u,v)
直径 d=max ecc(u)
半径 r=min ecc(u) (d≠2r)
中心 arg min ecc(u) (要求定义在点上)
绝对中心 (可以定义在边上)
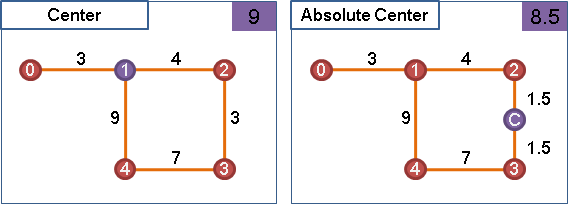
(12)、绝对中心 && 最小直径生成树
①绝对中心简介:
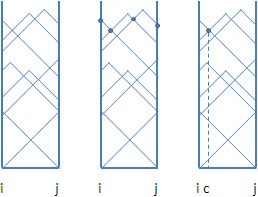
固定一条边(u,v),考虑上面的点p的偏心距。
假设第三个点是w, dis(p,u)=x
那么对应的折线为 min(x+dis(u,w), w(u,v)-x+dis(v,w))。
那么偏心距为n条折线的最大值形成的折线。
按左端点排序维护一下。
时间复杂度O(nm log n)
②最小直径生成树简介:
绝对中心的最短路树证明:
注意一棵树T有直径为半径的两倍(对绝对中心来说)。
如果最小直径生成树T’不包含绝对中心,那么取T’的绝对中心v,显然矛盾。
(13)、拓扑排序
每次去掉图中入度为0的点。时间复杂度O(n+m)。如果最后不为空集那么这个图不为DAG。 否则每个点入度不为0,即每个点可以选择一个前趋,沿着前趋走根据抽屉原理一定能找到相同点,也就是一个环。
①字典序最小的拓扑序
每个点有不同的标号,要使得拓扑序最小。将拓扑排序的队列改成优先队列即可。
②最小拓扑序的一个变种
使得最后的拓扑序中1的位置尽量靠前,如果相同比较2的位置,依次类推。首先考虑如何求1最早出现的位置,可以将原图反向,然后每次弹除了1之外的元素,直到队列只剩下1为止。这是反图中1的最晚的出现的位置,也就是原图中最早的。根据是否在队列里,这个图被分成两部分,在对应的图中用同样的方法处理2,依次类推。容易发现每次找尽量大的元素出队,能完成上述的过程。所以等价于反图最大字典序。
(14)、Hall’s marriage theorem简介:
对于一个二分图G=(X,Y,E),记S为X的一个子集,N(S)为所有S中所有点邻居的并集。
一个图有完备匹配当且仅当X的所有子集S都有|S|<=|N(S)|
对一般图的推广:

推论: 每个正则二分图都有完备匹配。
(15)、Kőnig's theorem简介:
最小点覆盖=最大匹配 (与最大流最小割定理等价)
最大独立集=点数-最大匹配 (独立集为点覆盖的补集)
最小边覆盖=最大独立集 (独立集中每个点需要一条边去覆盖)
(16)、DAG最小路径覆盖简介:
覆盖所有的边: 每条边下界设为1, 然后求最小流。
覆盖所有的点: 建立二分图,对于u->v的边,看做二分图中的(u,v’),然后答案为点数-最大匹配。
Dilworth 定理: 最大反链=最小链覆盖
(17)、强连通分量 && 双联通分量
①强连通分量简介:
Tarjan:
首先每个点根据DFS的时候访问的顺序进行标号,记作这个点的时间戳。
然后每个点维护一个low值,即这个点通过Tree edge和Back edge能访问到时间戳最小的点。
如果一个点的能访问到最早的点为这个点,就会形成一个新的强连通分量。
一个图将强联通分量缩起来将会形成一个DAG。
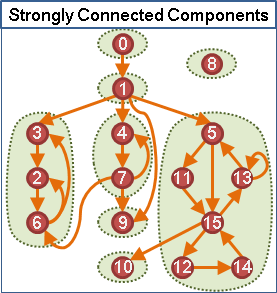
②代码(tarjan):
void tarjan(int pos){
vis[stack[++index]=pos]=1;//入栈并标记
LOW[pos]=DFN[pos]=++dfs_num;
for(int i=pre[pos];i;i=E[i].next){
if(!DFN[E[i].to]){
tarjan(E[i].to);
LOW[pos]=min(LOW[pos],LOW[E[i].to]);
}
else if(vis[E[i].to]) LOW[pos]=min(LOW[pos],DFN[E[i].to]);
}
if(LOW[pos]==DFN[pos]){
vis[pos]=0;
size[dye[pos]=++CN]++;//染色及记录强连通分量大小
while(pos!=stack[index]){
vis[stack[index]]=0;
size[CN]++;//记录大小
dye[stack[index--]]=CN;//弹栈并染色
}
index--;
}
}
③双联通分量简介:
点连通度: 最小的点集使得删去之后图不连通
边连通度: 最小的边集使得删去之后图不连通
如果一个图的点连通度大于1,那么是点双连通的,边连通同理。
双联通分量为图中的极大双联通子图。
(18)、割点和桥
①简介:
考虑DFS树,每条非树边对应着一个点到祖先的路径。对于一条非树边只要把对应的边打上标记即可。比如对于(u,v)这条非树边,只要在u点打上+1的标记,v点打上-1的标记。v到v的父亲的树边的覆盖次数为子树内所有标记的和。割点同理(注意特判根节点和叶节点)。
注意打标记这个过程可以在线完成。可以使用一个并查集维护当前双联通分量中的点,记录一下每个双联通分量中最高的点。然后对于一条非树边,暴力将这些点合并起来即可。因为一条边最多被合并一次,需要不超过O(m)次的并查集操作。边双联通分量缩完之后会形成一棵树。
②例(2-SAT):
一堆变量的二元限制,问是否存在合法的赋值。
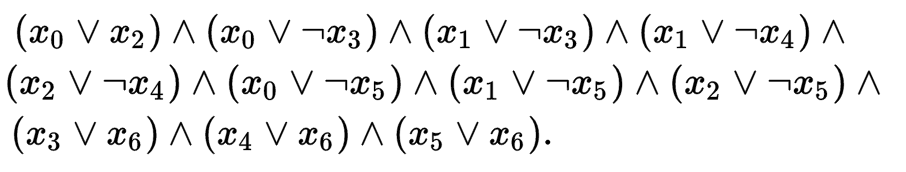
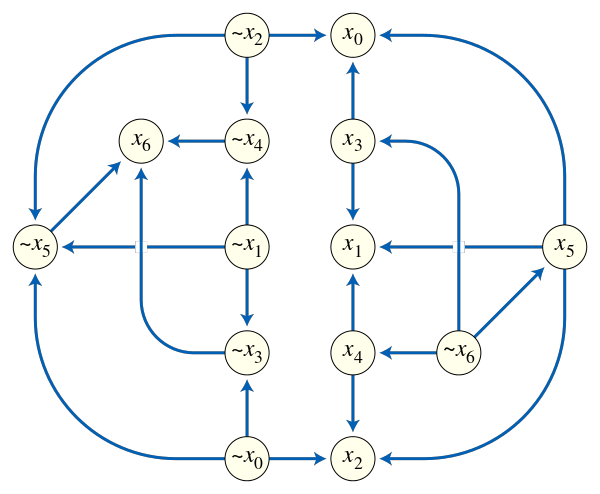
首先每个变量拆两个点,Xi和Xi’表示Xi=1或0对于Xi or Xj这样的限制,从Xi’向Xj连边,从Xj’向Xi连边,表示如果Xi取0,那么Xj要取1,反之亦然。同时对于Xi=1这样的限制可以转化为Xi or Xi,于是从Xi’向Xi连边,表示不能取Xi’。对于这样的图求强连通分量。有解的充要条件为对于每个变量Xi和Xi’不在同一个强连通分量里。求方案的时候,对于一个变量Xi和Xi’,只要取Tarjan算法中强连通分量早形成的即可。感性认识: 如果Xi能到达Xi’,那么Xi’的强连通分量会早形成。
(19)、图论例题整理(未完...):
Allowed Letters(CF 1009 G)代码实现:
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1e5+10;
const int M=63;
int m,x,len,l,t;
int a[N],ans[N],js[7],f[M+2][N];
char s[N],ch[9];
inline int read() {
int n=0,f=1;char ch=getchar();
while (ch<'0' || ch>'9') {if(ch=='-') f=-1;ch=getchar();}
while (ch<='9' && ch>='0') {n=(n<<3)+(n<<1)+ch-'0';ch=getchar();}
return n*f;
}
inline int work(int x) {
for(int k=0;k<=M;++k) {
int jc=0;
for(int i=0;i<6;++i)
if((k>>i)&1) jc+=js[i];
if(f[k][len]-f[k][x]<jc) return 0;
}
return 1;
}
int main() {
scanf("%s%d",s+1,&m);
len=strlen(s+1);
//预处理一下
for(int i=1;i<=len;++i) {
a[i]=M,ans[i]=-1;
++js[s[i]-'a'];
}
for(int i=1;i<=m;++i) {
scanf("%d%s",&x,ch);
l=strlen(ch),t=0;
for(int j=0;j<l;++j) t|=1<<(ch[j]-'a');
a[x]&=t;
}
for(int k=0;k<=M;++k)
for(int i=1;i<=len;++i) f[k][i]=f[k][i-1]+(bool)(a[i]&k);
for(int i=1;i<=len;++i) {
for(int j=0;j<6;++j) {
--js[j];
if(((a[i]>>j)&1) && work(i)) {
ans[i]=j;
break;
}
++js[j];
}
if(ans[i]==-1) {
printf("Impossible\n");
return 0;
}
}
for(int i=1;i<=len;++i) cout<<char(ans[i]+'a');
return 0;
}
Revmatching (TCO 2015 1A Hard)
Valid BFS? (CF 1037 D)
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<vector>
#include<queue>
#include<algorithm>
using namespace std;
const int N=2e5+10;
int n,x,y,res;
int vis[N],head[N];
vector<int> g[N],ans;
queue<int> q;
struct node {
int a,b,nxt;
}e[N];
inline int read() {
int n=0,f=1;char ch=getchar();
while (ch<'0' || ch>'9') {if(ch=='-') f=-1;ch=getchar();}
while (ch<='9' && ch>='0') {n=(n<<3)+(n<<1)+ch-'0';ch=getchar();}
return n*f;
}
inline int cmp(int x,int y) {
return e[x].b<e[y].b;
}
inline void init() {
for(int i=1;i<=n;++i) e[e[i].a].b=i;
for(int i=1;i<=n;++i) {
sort(g[i].begin(),g[i].end(),cmp);
for(int j=0;j<g[i].size();++j) res=g[i][j];
}
}
inline void bfs(int s) {
q.push(s);
vis[s]=1;
while (!q.empty()) {
int u=q.front();
q.pop();
ans.push_back(u);
for(int i=0;i<g[u].size();++i) {
int v=g[u][i];
if(vis[v]) continue;
vis[v]=1;
q.push(v);
}
}
}
inline int pd() {
for(int i=0;i<ans.size();++i)
if(e[i+1].a!=ans[i]) return 0;
return 1;
}
int main() {
n=read();
for(int i=1;i<=n-1;++i) {
x=read(),y=read();
g[x].push_back(y);
g[y].push_back(x);
}
for(int i=1;i<=n;++i) e[i].a=read();
if(e[1].a!=1) {
printf("No");
return 0;
}
init();
bfs(1);
if(pd()) printf("Yes");
else printf("No");
return 0;
}
Cycle (HDU 5215)
航空管制 (NOI 2010)
题目简述:
有n个航班依次起飞,一个时刻只能有一个飞机起飞,并且有m个限制:第一种限制,第i个飞机必须在c(i)的时刻前起飞。第二种限制,第i个飞机必须在第j个飞机之前起飞。
询问:
一个可行的起飞方案。每个飞机最早的起飞时间。n<=2e3, m<=1e4
Solution
倒过来变成每个飞机在某个时刻之后可以起飞。
第二问变成每个飞机最晚什么时候起飞。
直接用拓扑排序的做法即可。
ABland Yard (AGC 27 C)
题目简述:
给你一个有向图,每个点都标有01。问是否对于所有01串,都存在一条路径,使得将路径上经过的点的数字连起来得到01串。
Solution
这里只讨论二分图。
最大匹配: Hungarian/Hopcroft-Karp/Dinic
最大权匹配: KM/费用流
判断是否存在奇环,只要看是不是二分图即可。
判断是否存在偶环,首先看每条非树边对应的环是不是偶环。
如果存在那么就找到了偶环。
否则考虑如果两个奇环相交,那么去除中间部分就会形成一个偶环。
所以对于奇环的非树边只要暴力访问树边打上标记,如果已经有标记了就说明存在奇环。
时间复杂度O(n+m)
Cycling City (CF 295 E)
题目简述:
你有一个n个点m条边的无向图。(n, m<=2e5)
问是否存在两个点,使得这两个点之间有三条简单路,并且这三条简单路没有公共点。
Solution
如果两条非树边对应的环有交,那么一定可以找到这样的两个点。否则不存在。
Hangar Hurdles (CERC 16)
题目简述:
有一个n*n的网格图,上面有些格子可行,有些格子是障碍。(N<=1000 Q<=300000 )
有Q个询问,想把一个正方形箱子从(r1,c1)推到(r2,c2),问箱子最大的大小。(起点终点是正方形箱子的中点)
Solution
首先从障碍开始bfs,求出每个格子最近的障碍。然后变成了求一条路径,使得路径上的最小值最大。求最大生成树,然后在上面倍增询问即可。
Life of the Party (ONTAK 2010)
Allowed Letters(CF 1009 G)
题目简述:
你有6种字母,第i个字母有ci个。你要用这些字母排成一个字符串,其中有一些条件,第i个位置只能填某个字母的子集。问你能填出的字典序最小的字符串是什么。(sum ci<=10^5)
Solution
首先求出最大匹配,下面考虑左边点的情况。我们将匹配中的边从右往左连,不在匹配中的边从左往右连。这个时候一条增广路成为一条连续的路径。从每个左边未匹配的点还是遍历,如果被一个左边的点被访问到,说明存在一条增广路,也就是不一定在最大匹配中。所有没有被访问到的点一定在最大匹配中。
Revmatching (TCO 2015 1A Hard)
题目简述:
给定一个n个点的二分图,每条边有一个边权。找到一个边权和最小的边集,使得删掉这个边集之后不存在完备匹配。n<=20
Solution
根据Hall定理,只要存在一个集合S,使得|N(S)|<|S|,则不存在完备匹配。于是我们枚举S集合,然后贪心删除边集使得|N(S)|<|S|。
Bajtman i Okrągły Robin (ONTAK 2015)
题目简述:
有n个强盗,每个强盗会在时刻l到时刻r抢劫,会造成c的损失。在一个时刻,你可以选择抓一个强盗,强盗被抓住之后不会造成损失。你要抓尽量多的强盗使得损失尽量小。(n<=5000)
Solution
按强盗从大到小排序,贪心选取每个强盗能不能抓。判断一些强盗能不能抓完,可以按左端点排序,使用优先队列维护右端点。贪心算法的正确性: 考虑匈牙利算法,从大到小一个一个匹配,一个点一旦在匹配中,那么一直在匹配里面。
不知名例题
题目简述:
平面上有n个点(x_i,y_i),将这些点红蓝染色使得每行每列红蓝点个数的差不超过1。生成2^n的01串(这个串头尾相连),使得所有长度为n的01串都出现过。
不知名例题2
题目简述:
有n个点,每个点有个权值ai,两个点之间的边权为(ai+aj) mod M。问最小生成树。(N<=1e5,0<=M,a_i<=1e9)

