P1991 无线通讯网[最小生成树]

题目描述

国防部计划用无线网络连接若干个边防哨所。2 种不同的通讯技术用来搭建无线网络；

每个边防哨所都要配备无线电收发器；有一些哨所还可以增配卫星电话。

任意两个配备了一条卫星电话线路的哨所（两边都ᤕ有卫星电话）均可以通话，无论他们相距多远。而只通过无线电收发器通话的哨所之间的距离不能超过 D，这是受收发器的功率限制。收发器的功率越高，通话距离 D 会更远，但同时价格也会更贵。

收发器需要统一购买和安装，所以全部哨所只能选择安装一种型号的收发器。换句话说，每一对哨所之间的通话距离都是同一个 D。你的任务是确定收发器必须的最小通话距离 D，使得每一对哨所之间至少有一条通话路径（直接的或者间接的）。

解析

点赞最多的那篇题解提到了瓶颈生成树，个人觉得造成了一些不必要的引入和证明（当然有兴趣者可以进行学习），实际上就用联通块也可以解释得很清楚，个人感觉也没有什么问题。

那就来口胡一下

首先回顾kruskal算法求解最小生成树步骤：其运用贪心思想，每次加入最小边，直到所有点连通为止。

首先根据题意，这个图是一个完全图，我们要找一个存在限制条件的生成树。

那么对于本题，我们首先考虑没有卫星电话存在的情况，显然就是一个裸的最小生成树。我们来看加边过程的具体意义：每次加入一条没有使用过的最短边，且该边没有连接两个已经连通的哨所，那么这条边会将至少两个哨所相连。

接着我们来看一个这样的例子：

假设此时P=5，S=3。

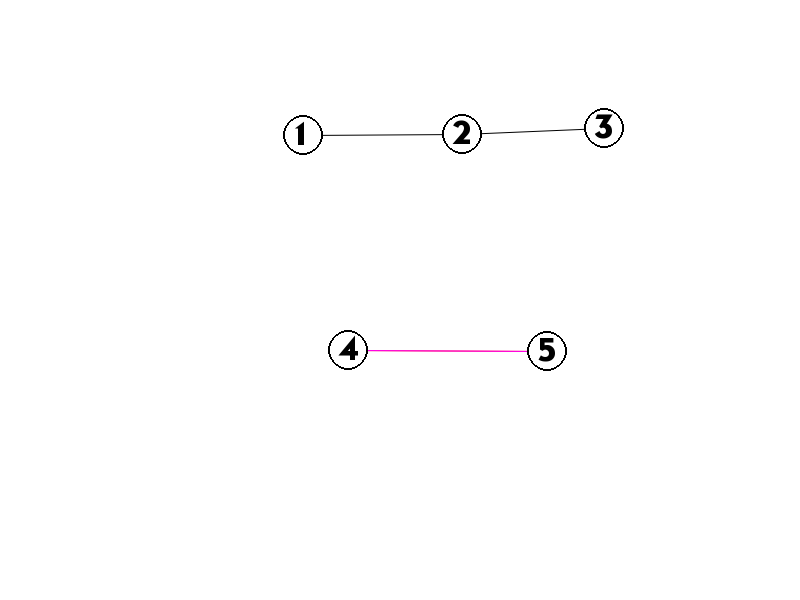
假设当前1、2、3为用无线电连接的哨所，4、5是用卫星电话连接的哨所。此时我们只要在1、2、3中某一个加一个卫星电话，就可以使它们全部连通。

因此我们不妨考虑先放无线电，加最短边加到联通块数量减为S为止（不考虑卫星电话哨所之间的连边，如上图紫边），此时还剩下S-1个点，如果我们在这些点放置无线电，显然会造成总体不优，所以我们在这些点中放卫星电话。

那么还剩一个卫星电话没有放怎么办？我们在之前放下去的无线电中找出来一个点放，并且还要使得答案不变坏，那这样一来所有点也就连通了。

参考代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<string>
#include<cstdlib>
#include<queue>
#include<vector>
#define INF 0x3f3f3f3f
#define PI acos(-1.0)
#define N 250010
#define MOD 2520
#define E 1e-12
#define IN freopen("data.in","r",stdin);
using namespace std;
inline int read()
{
	int f=1,x=0;char c=getchar();
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
	return x*f;
}
struct node{
	int x,y;
	double val;
	bool operator<(const node a)const{
		return val<a.val;
	}
}g[N];
struct dat{
	int x,y;
}a[N];
inline double fun(int x1,int y1,int x2,int y2){return sqrt((x2-x1)*(x2-x1)+(y2-y1)*(y2-y1));}
int s,p,fa[N];
inline int get(int x){return x==fa[x]?x:get(fa[x]);}
inline void merge(int x,int y)
{
	x=get(x),y=get(y);
	if(x!=y) fa[x]=y;
}
int main()
{
	s=read(),p=read();
	for(int i=1;i<=p;++i)
		a[i].x=read(),a[i].y=read(),fa[i]=i;
	int cnt=0;
	for(int i=1;i<=p;++i)
		for(int j=i+1;j<=p;++j){
			double z=fun(a[i].x,a[i].y,a[j].x,a[j].y);
			g[++cnt].x=i,g[cnt].y=j,g[cnt].val=z;
		}
	sort(g+1,g+cnt+1);
	double ans=0;
	int tot=p;
	for(int i=1;i<=cnt;++i){
		int x=get(g[i].x),y=get(g[i].y);
		if(x==y) continue;
		if(tot==s) break;
		tot--;
		merge(x,y);
		ans=g[i].val;
	}
	printf("%.2lf\n",ans);
	return 0;
}