浅谈最大子矩阵
浅谈最大子矩阵问题
【最大子矩阵问题】
最大子矩阵问题是一类求解某个矩阵中最大符合条件的子矩阵的问题,一般的条件有子矩阵不能覆盖障碍点、子矩阵的形状等。
【极大化思想】
这里首先解释几个概念:
- 有效子矩阵:满足题目要求的子矩阵。
- 极大子矩阵:满足题目要求的、边界无法再扩张的子矩阵。
- 最大子矩阵:极大子矩阵中最大的一个。
在许多问题中,我们常常见到形如“使xx面积最大”“找到最大的矩形”的提问,实际上就是要我们求解最大子矩阵。
所谓极大化思想,其实就是枚举极大子矩阵,找到其中最大的一个。
【如何求解极大子矩阵】
上面提到要枚举极大子矩阵,那么显然,前提是我们要求解所有极大子矩阵。一般而言,我们有两种算法来求解所有极大子矩阵。
我们首先定义一些符号:\(n\)表示矩阵的高,\(m\)表示矩形的宽,\(k\)表示矩形中障碍点的数量。
边界扩展法(我瞎起的名字)
根据极大子矩阵的定义,其边界无法再扩张,那么显然其边界要么在障碍物所在行/列(即恰好覆盖障碍点),要么与整个矩阵的边界重合。
因此,我们不妨从障碍点入手,不断扩张极大子矩阵,扩展它的边界。显然有一种做法就是枚举所有可能构成矩形的边界,找出最大子矩阵,但是复杂度感人。那么如何优化呢?
我们要使得这个优化尽量少的枚举不是极大子矩阵的矩阵,还要确保这些子矩阵是合法的。
我们不妨线性的逐行扩展最大子矩阵的某一个边界,然后根据其它障碍点的位置维护其它边界的位置。
具体而言,就是先对所有障碍点按列升序排序,然后依次枚举这些障碍点,以此次枚举的障碍点所在的列作为极大子矩阵左边界,然后将右边界向右扩展,在扩展右边界时,我们还要维护上下边界,使得这些子矩阵满足合法性。
具体如何维护上下边界,这边窝弄了几张大佬的图(不要打我):
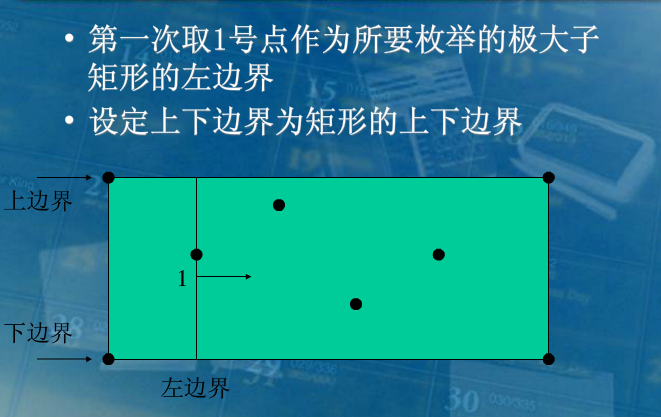
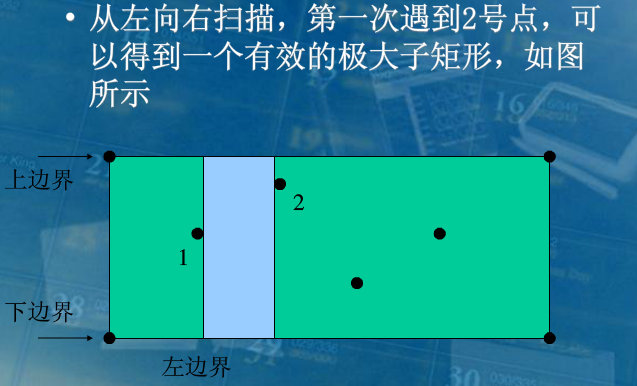
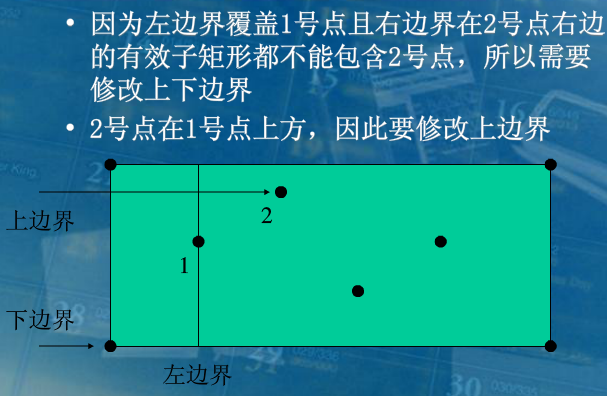
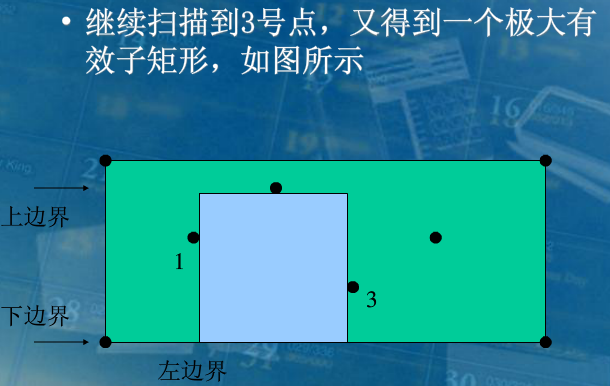
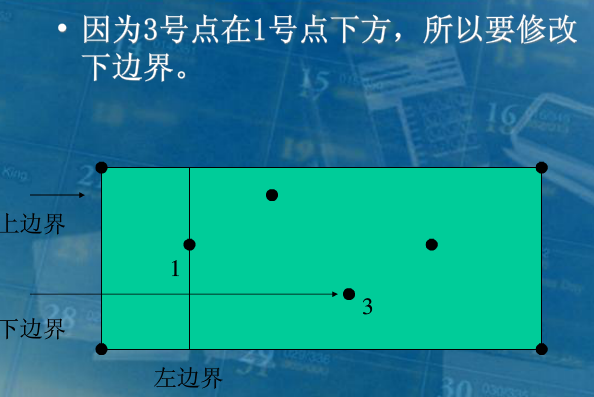
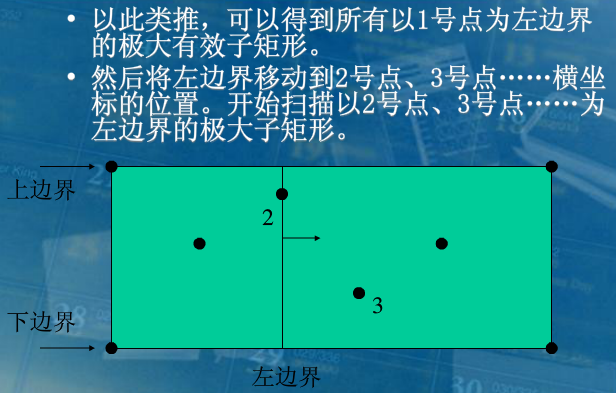
这个已经讲的很清楚了,我就不必多言了。
例题 P1578 奶牛浴场
题目描述
由于John建造了牛场围栏,激起了奶牛的愤怒,奶牛的产奶量急剧减少。为了讨好奶牛,John决定在牛场中建造一个大型浴场。但是John的奶牛有一个奇怪的习惯,每头奶牛都必须在牛场中的一个固定的位置产奶,而奶牛显然不能在浴场中产奶,于是,John希望所建造的浴场不覆盖这些产奶点。这回,他又要求助于Clevow了。你还能帮助Clevow吗?
John的牛场和规划的浴场都是矩形。浴场要完全位于牛场之内,并且浴场的轮廓要与牛场的轮廓平行或者重合。浴场不能覆盖任何产奶点,但是产奶点可以位于浴场的轮廓上。
Clevow当然希望浴场的面积尽可能大了,所以你的任务就是帮她计算浴场的最大面积。
解析
首先要注意这道题神坑的坐标系统,输入中给出的每个位置是一个点,而不是一个格子(话说您家产奶点是没有面积的),因此,”但是产奶点可以位于浴场的轮廓上“的意思就是最大子矩阵的边界可以踩在障碍点上面。
然后就是套上面的算法(似乎这题好多题解都被\(hack\)掉了,怕怕)
参考代码
#include<cstdio>
#include<iostream>
#include<cmath>
#include<cstring>
#include<ctime>
#include<cstdlib>
#include<algorithm>
#include<queue>
#include<set>
#include<map>
#define N 5010
using namespace std;
struct node{
int x,y;
}a[N];
int n,m,t;
inline bool cmp(node a,node b)
{
if(a.y==b.y) return a.x<b.x;
return a.y<b.y;
}
inline bool cmp2(node a,node b)
{
return a.x<b.x;
}
int main()
{
scanf("%d%d%d",&n,&m,&t);
for(int i=1;i<=t;++i) scanf("%d%d",&a[i].x,&a[i].y);
a[++t].x=0,a[t].y=0;//注意,此处加上这个可以保证最大子矩阵最大为整个矩阵
a[++t].x=n,a[t].y=0;
a[++t].x=0,a[t].y=m;
a[++t].x=n,a[t].y=m;
if(t==0){
printf("%d\n",n*m);//加个特判,以免翻车
return 0;
}
sort(a+1,a+t+1,cmp);
int ans=0;
for(int i=1;i<=t;++i){
int u=n,d=0,maxx=0;
for(int j=i+1;j<=t;++j){
int w=a[j].y-a[i].y;
int h=u-d;
maxx=max(maxx,w*h);
if(a[j].x>a[i].x&&a[j].x<u) u=a[j].x;
else if(a[j].x<a[i].x&&a[j].x>d) d=a[j].x;
else if(a[j].x==a[i].x) u=d=a[j].x;
}
ans=max(maxx,ans);
}
for(int i=t;i>0;--i){
int u=n,d=0,maxx=0;
for(int j=i-1;j>0;--j){
int w=a[i].y-a[j].y;
int h=u-d;
maxx=max(maxx,w*h);
if(a[j].x>a[i].x&&a[j].x<u) u=a[j].x;
else if(a[j].x<a[i].x&&a[j].x>d) d=a[j].x;
else if(a[j].x==a[i].x) u=d=a[j].x;
}
ans=max(maxx,ans);
}
sort(a+1,a+t+1,cmp2);
for(int i=1;i<t;++i) ans=max(ans,(a[i+1].x-a[i].x)*m);//不知道为啥竖着扫不对
cout<<ans<<endl;
return 0;
}
总结:可以看到,这个算法本身是基于障碍点的,因此适用于障碍点明显较少的题目,复杂度\(O(k^2)\)
悬线法
对于这个算法,一个字,妙,俩字,好用,三字,太强了,四字,好写好想。
你可以看到很多二维\(dp\)的题目都可以用这个算法水过去。
简单来讲,悬线法有一个点像上面的思路,即所谓逐行扩展边界,维护其它边界。具体到悬线法,做法就是逐行扫一遍整个矩阵,计算每个点向右/左/上能够扩展的最大距离,实际上就是维护了这个点所在极大子矩阵的边界。
思路就是这么简单,实际实现也非常简单,我们看一道例题。
P1169 [ZJOI2007]棋盘制作
题目描述
国际象棋是世界上最古老的博弈游戏之一,和中国的围棋、象棋以及日本的将棋同享盛名。据说国际象棋起源于易经的思想,棋盘是一个8×8大小的黑白相间的方阵,对应八八六十四卦,黑白对应阴阳。
而我们的主人公小Q,正是国际象棋的狂热爱好者。作为一个顶尖高手,他已不满足于普通的棋盘与规则,于是他跟他的好朋友小W决定将棋盘扩大以适应他们的新规则。
小Q找到了一张由N×M个正方形的格子组成的矩形纸片,每个格子被涂有黑白两种颜色之一。小Q想在这种纸中裁减一部分作为新棋盘,当然,他希望这个棋盘尽可能的大。
不过小Q还没有决定是找一个正方形的棋盘还是一个矩形的棋盘(当然,不管哪种,棋盘必须都黑白相间,即相邻的格子不同色),所以他希望可以找到最大的正方形棋盘面积和最大的矩形棋盘面积,从而决定哪个更好一些。
于是小Q找到了即将参加全国信息学竞赛的你,你能帮助他么?
解析
应用悬线法。
具体做法我们一般要维护任意点\((i,j)\)的三个性质:在保证题目给出性质的前提下,该点可以向左扩展到的最远的点\(l[i][j]\),向右扩展到的最远的点\(r[i][j]\),向上扩展到的最远的点\(up[i][j]\)。
状态转移方程:
在这之前,我们要预处理出单行(可以理解做)每个点的和。
参考代码
#include<cstdio>
#include<iostream>
#include<cmath>
#include<cstring>
#include<ctime>
#include<cstdlib>
#include<algorithm>
#include<queue>
#include<set>
#include<map>
#define N 2010
using namespace std;
int mp[N][N],l[N][N],r[N][N],up[N][N],n,m;
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i)
for(int j=1;j<=m;++j) scanf("%d",&mp[i][j]),l[i][j]=r[i][j]=j,up[i][j]=1;
for(int i=1;i<=n;++i)
for(int j=2;j<=m;++j)
if(mp[i][j]!=mp[i][j-1])
l[i][j]=l[i][j-1];
for(int i=1;i<=n;++i)
for(int j=m-1;j>0;--j)
if(mp[i][j]!=mp[i][j+1])
r[i][j]=r[i][j+1];
int ans1=0,ans2=0;
for(int i=2;i<=n;++i)
for(int j=1;j<=m;++j){
if(mp[i][j]!=mp[i-1][j]){
l[i][j]=max(l[i][j],l[i-1][j]);
r[i][j]=min(r[i][j],r[i-1][j]);
up[i][j]=up[i-1][j]+1;
}
int w=r[i][j]-l[i][j]+1;//宽
int h=up[i][j];//高
int t=min(w,h);
ans1=max(ans1,t*t);
ans2=max(ans2,w*h);
}
cout<<ans1<<endl;cout<<ans2<<endl;
return 0;
}
总结:显然,悬线法不再基于障碍点,而是整个矩阵,也因而适用于整个矩阵较小,障碍点较多的情况。


