组合与计数

组合数学与计数

即使这是小奥，但也阻止不了窝再学一遍（笑

总的来说，计数问题在\(NOIp\)中还是占有一席之位的。

快速过一遍。

基本计数原理

一些原理：加法原理，减法原理，乘法原理。

容斥原理：

很好理解，画个Venn图就很快明白了。

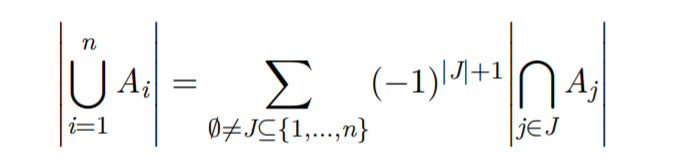
略提摩根律：

$C_S(P∩Q)=(C_SP)∪(C_SQ)C_S(P∩Q)=(C_SP)∪(C_SQ) \( \)C_S(P∪Q)=(C_SP)∩(C_SQ)$

计数问题常见技巧：

• 当直接统计具有一种性质的事物个数较为困难时，考虑统计不具有这种性质的事物个数，再用总数减去这个值。
• 把正向的解集变成其补集的交集，二者等价。
• 直接算并集大小较为困难，但是算交集大小相对容易（或者相反），有时也可用摩根律转换为补集的交或并。
• 当我们需要计算一些带特殊条件的方案数时，可以用一些等价替代的方法。具体来讲，我们构造一个双射（一一映射），将每一种原问题的方案映射为新问题的一种方案，并使答案更容易计算。

捆绑法：也称整体法，在计数时，如果要求若干物品相邻，则可以将它们作为一个整体来进行计数。

插空法：如果要求若干物品两两不相邻，可以先将其他物品放好，然后将这些物品插入空当中，进行计数。

隔板法：将不可区分物品分配问题/不定方程整数解问题转化为插板组合问题。

看几个例题。

1.把 n 个相同的苹果分给 k 个人，要求每个人至少分到一个，求方案数。

解：应用隔板法，这个问题相当于将\(n\)个不同物品划分成\(k\)份，即\(\dbinom{n-1}{k-1}\)。

其实可以看作解不定方程\(\sum^n_{i=1}x_i=n\)这个方程的解集的元素总数。

2.变式：把 n 个相同的苹果分给 k 个人，每个人可以分到0个，求方案数。

解：仍然是隔板法，我们想象加入\(k\)个空气苹果（极限情况为没有一个人拿到苹果），分到这种苹果的人相当于分到0个苹果，那么问题转化为将\(n+k\)个物品划分成\(k\)份，即\(\dbinom{n+k-1}{n-1}\)。

排列组合

根据乘法原理，容易得出：

\[\dbinom{n}{m}=C_n^m=\frac{n!}{m!(n-m)!}\\ P_n^m=\frac{n!}{(n-m)!} \]

几个简单的性质：

\[\dbinom{n}{0}=1,\dbinom{n}{1}=n,\dbinom{n}{2}=\frac{n(n-1)}{2}\\ \dbinom{n}{m}=\dbinom{n}{n-m}\\ \frac{m}{n}\dbinom{n}{m}=\dbinom{n-1}{k-1} \]

组合数递推公式：

\[\dbinom{n}{m}=\dbinom{n-1}{m-1}+\dbinom{n-1}{m},k>0 \]

一般组合数求法：

• 递推

for(int i=0;i<n;++i){
	C[i][0]=1;
    for(int j=1;j<=i;++j){
		C[i][j]=C[i-1][j-1]+C[i-1][j];
    }
}

• 逆元（在模p的意义下）

前置技能：对于任意一个整数\(x\)，它在模\(p\)意义下除以一个整数\(y\)的答案等价于它乘上除数的逆元。

\(a/b\mod{p}=a*inv(b) \mod{p}\)，其中 \(inv\)表示逆元。

\[\begin{align} \dbinom{n}{m}\mod p &=\frac{n!}{m!(n-m)!}\mod p\\ &=n!*inv(m!)*inv((n-m)!)\mod p\\ &=n!*(m!*(n-m)!)^{p-2}\mod p \end{align} \]

用快速幂即可。

• lucas

我不会。

二项式定理

这个定理其实是显然的。

\[(x+y)^n=\sum^n_{k=0}\dbinom{n}{k}x^{n-k}y^k \]

再看几个例题。

1.错位排列：有 n 个信封和 n 封信，一一对应，求把每封信都装错信封的方案数。

解：利用容斥原理，考虑它们补集的交集，这显然可以用容斥去做。对于指定的\(k\)封信，我们假设它们装对了，那么方案数是\((n-k)!\)种。而指定\(k\)封信的方案数是\(\dbinom{n}{k}\)，根据乘法原理，我们得到答案：\(\sum^{n}_{k=0}(-1)^k\dbinom{n}{k}(n-k)!=\sum^{n}_{k=0}(-1)^k\frac{n!}{k!}\)

2.JSOI2011 分特产

有 n 个同学，m 种特产，每种特产有 $a_i $个，需要分给每个同学，满足每个人至少分到一个，求方案数。
n, m ≤ 1000, \(a_i\) ≤ 1000。答案对 \(10^9 + 7\) 取模。

解：这其实是一道变种的隔板法，我们把需要的答案统计起来即可。考虑一种容斥的做法，即像上面那题一样，考虑补集的交集。假设有\(k\)个同学一个土特产都没分到，方案数为\(f(k)\)。易得出答案：\(\sum^n_{k=0}(-1)^k\dbinom{n}{k}f(k)\)。考虑\(f(k)\)，由于有\(m\)种土特产，它们对解的贡献相互独立，所以我们对每种土特产计一次答案，由上面的变式得有空位的插板的方案总数：\(f(k)=\prod^m_{i=1}\dbinom{a_i+(n-k)-1}{n-k-1}\)

不难看出，这些题目都具有相同的性质，即正面求解集较难，我们便尝试转换为求解集的补集的交集，然后用容斥去解这个交集。

容斥在省选中好像算比较简单的？不管他，我菜。

其实还是比较好理解的。