hdu 1394 Minimum Inversion Number(逆序数对) ： 树状数组 O(nlogn)

http://acm.hdu.edu.cn/showproblem.php?pid=1394  //hdu 题目

 

Problem Description

The inversion number of a given number sequence a1, a2, ..., an is the number of pairs (ai, aj) that satisfy i < j and ai > aj.

For a given sequence of numbers a1, a2, ..., an, if we move the first m >= 0 numbers to the end of the seqence, we will obtain another sequence. There are totally n such sequences as the following:

a1, a2, ..., an-1, an (where m = 0 - the initial seqence)
a2, a3, ..., an, a1 (where m = 1)
a3, a4, ..., an, a1, a2 (where m = 2)
...
an, a1, a2, ..., an-1 (where m = n-1)

You are asked to write a program to find the minimum inversion number out of the above sequences.

 

给定一个数组 a1,a2....an，定义逆序数对（i，j）满足条件 i< j 且 ai > aj。
现在题目给你数组，求他的所有循环数组的逆序数对中最少的是多少。
所谓循环数组即为：

a1, a2, ..., an-1, an (从1开始的初始数组) 
a2, a3, ..., an, a1 (从a2开始到an，再加上a1) 
a3, a4, ..., an, a1, a2 (a3开始到an，再连上a1和a2) 
... 
an, a1, a2, ..., an-1 (an，然后从a1到a(n-1))

 

Input

The input consists of a number of test cases. Each case consists of two lines: the first line contains a positive integer n (n <= 5000); the next line contains a permutation of the n integers from 0 to n-1.

 

输入有多组数据. 每个测试案例的第一行是一个数n(n <= 5000)表示数组长度: 接下来一行是n个数表示数组内容，数组内的数字是0~n-1以内的数，且没有重复 

Output

For each case, output the minimum inversion number on a single line.

对于每个样例输出一个数字表示答案 

 

思路：

首先是怎么求其中一个序列的逆序数对

假设序列开始一个数都没有

每添加一个数之前计算序列有多少数大于该数（即在该位添加时会增加多少对逆序数）<===算作一个状态

将所有状态相加即是该序列的逆序数对数量

拿样例来说

 

 

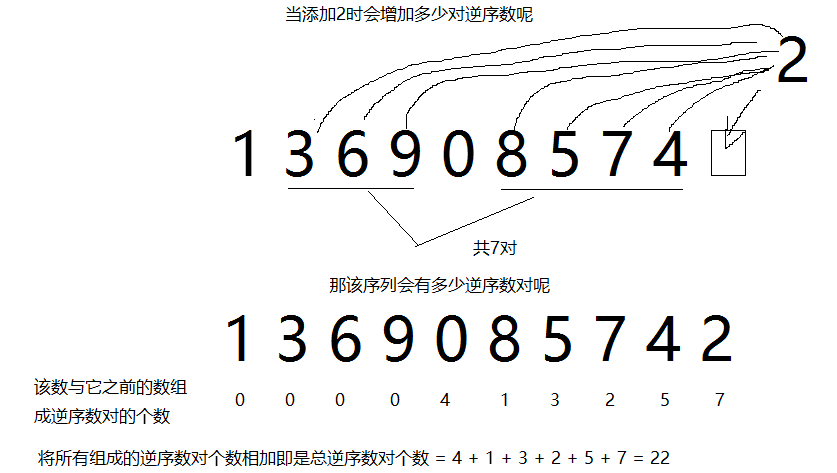
那怎么高效的算出所有循环数组的逆序数对个数

观察不难发现，当a0移动到an-1末尾后减少了它之后能与它形成逆序数对的个数(比它小的数)

                                               增加了在末尾时它之前能与它形成逆序数对的个数(比它大的数)

由于下一个循环数列必定是将头移至尾，所以减少的个数为比它小的个数

                                                                        增加的个数为比它大的个数

因为数是不会重复的且为0~n-1共n个，所以 a[i] - 1就是序列中比它小的数的个数

                                                                      n - a[i]就是序列中比它大的数的个数

 

代码：

 

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

const int maxn = 5005;

int c[maxn], a[maxn], n;

inline int lowbit(int x){
    return x&(-x);
}

void update(int i, int value){
    while(i <= n){
        c[i] += value;
        i += lowbit(i);
    }
}

int sum(int i){
    int s = 0;
    while(i > 0){
        s += c[i];
        i -= lowbit(i);
    }
    return s;
}

int main(){
    while(~scanf("%d", &n)){
        for (int i = 1; i <= n; ++i){
            c[i] = 0;
        }
        int s = 0; //最开始逆序数对数为0
        for(int i = 1; i <= n; i ++){
            scanf("%d", &a[i]);
            a[i] ++; //树状数组从1开始 数据范围(0~n-1)
            s += (sum(n) - sum(a[i])); //找出所有比a[i]大的数的逆序数对数
            update(a[i], 1); //记录这个数
        }
        int ans = s;
        for(int i = 1; i < n; i ++){ 
            s += (n - a[i]*2 + 1); //比较完后因为 n 个数范围(0~n-1)且不重复， 所以比a[i] 小的数为a[i] - 1;
            // 每次将头元素移至末尾都会减少比头小的数(a[i] - 1)个逆序数，增加比头大的数(n - a[i])个逆序数
            // 所以增加的逆序数为 n - a[i] * 2 + 1  [+(n - a[i]) -(a[i] - 1)]
            if(ans > s) //记录更少的逆序数对数
                ans = s;
        }
        printf("%d\n", ans);
    }
    return 0;
}