寒假橄榄计划😢
指的是记录自己被橄榄的时刻😰
[JOISC2020] 掃除
Solution
md，太sb了，不想写这个沟是题的题解了。
[CCO2020] Shopping Plans
Solution
读错题了。😅
我们首先考虑 \(m=1\) 的情况，可以发现的是，我们大概是可以用小根堆去处理的。很套路的做法就是设 \((x,y,z)\) 表示前缀 \([1,x]\) 都选了，当前这个节点在 \(y\)，下一个在 \(z\)。然后我们每次可以把 \(y\) 往后面移一个（\(< z\)），或者把 \(x\) 挑出来，状态自然就是转移到 \((x,y+1,z)\) 以及 \((x-1,x+1,y)\)。当然还有加点进去的情况，当 \(z=\infty,y=x+1\) 的时候，我们可以 \((x-1,x,\infty)\to (x,x+1,\infty)\)。
然后考虑 \(m>1\) 的情况，发现还是差不多的处理。因为种类之间相对独立，我们对于第 \(t\) 个种类的第 \(i\) 大的答案设为 \(s_{t,i}\)。我们构造的话就是选一个位置开始从 \(s_{t,0}\to s_{t,1}\)，然后不断变化，指 \(s_{t,i}\to s_{t,i+1}\) 或者到 \((t+1,1)\)，对于中间会跳过的情况，我们可以 \(-(s_{t,1}-s_{t,0})+(s_{t+1,1}-s_{t+1,0})\)。
说白了，就是两个非常套路的结合，做不出来纯属我自己脑瘫，或者说不是很熟吧。/kk
CF1654G Snowy Mountain
Solution
md，这种sb题目都做不来了😅
设 \(h_u\) 表示 \(u\) 节点出发到最近的黑点的距离。一个很明显的结论是对于点 \(u\)，如果它能到 \(x\) 并且 \(x\) 存在相邻节点使得 \(h\) 相同，那么能产生的最大贡献即是 \(2h_u-h_x\)，道理也很显然，前面 \(u\) 留下来的势能可以在 \(x\) 节点消耗尽，每个能量就可以操作两次。那么我们很显然就需要对于每个 \(u\) 找到最小的 \(h_x\)。
另一个重点是，存在 \(\sum_x h_x\ge n\)（\(x\) 需要满足存在相邻节点 \(h\) 相同）。因为你每次相同都需要多余的 \(h_x\) 个节点。所以有用的 \(x\) 最多只有 \(\sqrt n\) 个。那么我们每次 01 BFS 找一下能够抵达他们的节点，更新一下就好了。
[AGC018F] Two Trees
Solution
天才小子题目，难以想出的。😥
我们先考虑一下如何判断 IMPOSSIBLE。似乎对于同一个点在两棵树的儿子个数奇偶性不同时，就会爆炸。然后就不会了。/kk
考虑天才建图，我们将两棵树的根用一个节点连接，然后同一个节点如果度数为奇数，那么将两棵树的这个节点连接，不妨把这种边成为横边，可以发现这样每个节点都是偶数度数了。然后我们跑欧拉回路，横边如果左往右就把对应节点设为 \(1\)，否则设为 \(-1\)。其余节点设为 \(0\)。
考虑其正确性，可以发现的是，对于一个节点，一定会出入其子树内偶数次，其中有一次是从父亲进入，剩余次数都是从横边出入，那么可以发现的是，这个子树里面的差就是 \(\pm 1\)，即满足条件。
感觉这种题目知道怎么做了之后就会觉得很套路，毕竟先判断一定无解，然后再建图跑欧拉回路，这样的步骤确实很套路，但是自己思考的时候就很难想到。/kk
「雅礼集训 2017 Day1」字符串
Solution
还是天才小子题目。已经受不了图论了💀
首先我们可以考虑到 \(m\le 2n-1\) 的时候是一定有解的，这个比较显然。然后考虑如何暴力判断，我们似乎可以把每个环找出来。一种找法是我们枚举一个点作为根，然后在图上搜出所有的环，当一个长度 \(r\) 被找到 \(2r+1\) 次的时候显然就会有解。因为一个环会被找到 \(2r\) 次。
发现这样做是指数级别的算法。不过我们可以发现，如果我们先判断一下一个点在不返回父亲的情况下能否到根的话，复杂度就会变成 \(\Theta(n^4)\)。因为这样就能直接找到环，不会有多余的复杂度浪费。
然后就是天才部分了。我们考虑随机删掉 \(\sqrt n\) 条边，那么一条边被删除的概率就是 \(\dfrac{\sqrt n}{m}=\dfrac{1}{\sqrt n}\)。考虑极限情况，即 \(3\sim n\) 的环都出现过，那么我们考虑还保留的环的个数就是： \(\sum_{i=3}^{n} (1-\dfrac{1}{\sqrt n})^i<\sqrt n\)。
因为期望意义下是 \(<\sqrt n\) 的，意味着有情况是会剩余 \(\sqrt n\) 个环，那么在这种情况下在删除 \(\sqrt n\) 条边就一定可以保证不会再存在环了。那么我们就可以知道，当 \(m\ge n+2\sqrt n\) 的时候是一定有解的。
考虑到我们可以把链缩成一个点，所以我们可以只保留 \(\mathcal O(\sqrt n)\) 个节点，再套用一下上面的算法，我们就可以做到 \(\Theta(n^2)\) 了。
[HAOI2017]字符串
Solution
其实不难，但是感觉想到建ACAM是一个难以想到的步骤，一直在想SA/SAM。/jk
我们考虑到其实就想到两个串相等其实就等价于 \(\text{lcs+lcp}+k\ge |w|\)。那么我们建了ACAM之后，考虑一个长度为 \(l\) 的串与 \([i,i+l-1]\) 能否匹配，那么我们可以枚举 \(j\) 使得 \([i,j]\) 与 \(l\) 的前缀相同，然后 \([j+k+1,i+l-1]\) 与 \(l\) 的后缀相同。我们考虑放在ACAM上面进行考虑，那么我们可以考虑枚举 \(j\)，然后前面匹配其实相当于在正向的 ACAM 上面匹配的过程，后面匹配就是在反向 ACAM 上面匹配的过程。
考虑如何统计答案，似乎只能对 \(j\) 进行计数，那么考虑它对应前缀 \([1,t]\) 指的是询问串的长度为 \(t\) 的前缀）。那么相当于 \([1,j]\)（模式串） 在 \([1,t]\) 的子树中（指ACAM上），且 \([j+k+1,n]\) 在 \([t+k+1,l]\) 的子树中。这个可以离线下来之后 \(\Theta(n\log n)\) 处理。但是问题是会算重，那么我们减一下 \(+k\) 的贡献就好了，相当于保证后缀匹配的是最长的，这样就唯一统计了。
似乎还是有点难想？/yiw 感觉保证唯一这一步可能确实比较难以想到。
「ROI 2017 Day 2」学习轨迹
Solution
其实是可做题，但是时间有限还是被橄榄了😖
我们发现答案至少是 \(\max (\sum x_i,\sum y_i)\)。下文称一个前缀和 \(\ge \sum a_i/2\) 的位置叫做 \(a_{1,2,..}\) 的中点。如果两个学校都会选的话，最优情况一定有一边是跨过中点的。我们不妨假设为 \(a_{1,2,...,n}\)。
那么我们可以发现的是，我们可以枚举 \(b\) 数组选出来的 \(r\)，然后考虑如何维护每个 \(l\) 对应的答案。发现其实就是维护单调栈的过程，左边禁选的位置是个单调下降的栈，右边单调上升。然后用线段树维护一下就好了。复杂度 \(\Theta(n\log n)\)。
当然，看不出第一个性质也可以中点分治解决。我做不出来纯属我自己nt。😐 upd: 似乎不能中点分治算？🤔
「2018 集训队互测 Day 5」小 H 爱染色
Solution
md，思考时间还是太少了，应该多想一会的。
可以看出，答案就是：
那么我们其实就是需要求出 \(\sum_{a=0}^{n-1} \binom{n-a}{m}^2F(a)\)。看着确实是不太好算。但是我们可以注意到的是，\(\dbinom{n-a}{m}=\dfrac{(n-a)^{\underline{m}}}{m!}\)，这是一个关于 \(a\) 的 \(2m\) 次方多项式。所以上面那个就是关于 \(a\) 的 \(3m+1\) 次方多项式。
注意到需要求出 \([0,3m+1]\) 位置的 \(F(i)\)，所以 \(\text{ntt}\) 优化一下即可。
yww 与校门外的树
Solution
mdsb题，说实话还是思考时间不够。不过其实思考时间更多能不能做出来也不知道捏🤔
其实可以看出的是，每个连通块一定是连续的一段，并且值域连续。证明的话可以考虑每次加入最小值，那么后面一段都会被合并起来。
计算的话就很简单了，注意到我们设 \(F(x)\) 表示长度为 \(n\) 的连通块的方案数的生成函数，再设 \(G(x)=\sum_{i} i!x^i\)，可以看出 \(\frac{1}{1-F}=G\)。然后再设 \(H(x)=\sum_{i} F(x)[x^i]i\)，答案就是 \([x^n]H(x)\)。多项式求逆顺便算一下就好了。
CF1168E Xor Permutations
Solution
之前 AKsen 拉过，但是因为不太懂原理没有做。今天看到湘妹写的博客就突然明白了😣
其实就是数值与位置的一个最大匹配，使得异或值没有相同值。然后用随机匹配一下，如果找不到未填的合法位置，就随机一个未填的位置填上去，然后把之前出现过的值对应的边断掉即可。其实主要思想还是随机化最大图最大匹配。
CF1209G2 Into Blocks (hard version)
Solution
之前考过，但是没有补😃
其实主要问题还是不好想的转化，以及转化之后线段树的维护。我们考虑到，对于一个颜色 \(c\)，如果出现为 \([l_c,r_c]\)，那么我们将 \([l_c,r_c)\) 都加 \(1\)，那么两个 \(0\) 之间的一段就是独立的一段。可以看出的是，这一段一定只能保留一个颜色。
所以我们把每个颜色的出现次数放在第一次出现位置，然后一个独立的段贡献就是其最大值，答案就是减去每一个独立的段的贡献的和。维护的话直接用线段树维护即可。还是老套路，把维护 \(0\) 变成维护最小值，即维护最小值，最大值（两个不是针对同一个数组），最左边最小值左边的最大值，最右边最小值右边的最大值，最左边最小值和最右边最小值中间的贡献之和。然后用 set 维护一下出现位置即可。
其实懂了之后就不难，但是确实挺难想的。educational。😋
[SNOI2020] 区间和
Solution
终于明白了吉司机线段树复杂度的证明了🥰（虽然和这个题关系不大。我们关注线段树一个段的不同颜色，视为势能，可以发现每次取 \(\max,\min\) 修改，向下递归的段至少减 \(1\)，而每次未被完整覆盖的段最多 \(+1\)，所以复杂度就是 \(\Theta(n)\) 的。
考虑这个题，很显然最大子段和需要我们维护线段树上每个段的最大前缀和和最大后缀和，发现只修改最小值的时候不好处理。不过可以发现的是，每个段的最大前缀/后缀和的长度一定是单调不减的，所以我们只需要快速判断一个段是否会改变然后直接保留修改即可。
考虑最大前缀和的修改。具体来说，当只有最小值增加 \(v\) 时，如果最大值为 \(s_1\)，其最小值个数为 \(c_1\)，存在 \(s_2\)，最小值个数为 \(c_2\)，使得 \(s_1>s_2,c_1<c_2\)，那么当：
的时候会改变，我们也只需要该值即可。
upd. 被hack了，还需要维护最大子段和在多久会被改变。
CF1458C Latin Square
Solution
被 2700 踩爆了 😋
主要问题还是在 I/C 怎么处理上面，发现对于 \(i,j\)，我们视其为三维空间里的一个点 \((i,j,a_{i,j})\)，那么 I 即是交换后两维，C 即是交换前两维。然后打一下标记维护一下即可。
CF793F Julia the snail
Solution
没想到会被这种题打败😇 离线下来按 y 来，用势能线段树维护每个 x 的答案即可。
[HNOI/AHOI2018]排列
Solution
我们发现其实题目就相当于我们连 \((a_i,i)\)，表示排列里面 \(a_i\) 必须在 \(i\) 之前。可以发现的是，如果出现了环，那么一定无解，所以一定会是一颗以 \(0\) 为根的树，然后要求父亲一定要在儿子之前被选。那么问题就是如何确定顺序。
可以发现的是，对于当前权值最小值，在父亲加入序列之后一定会立马选上，那么问题就是如何确定一个块和一个块之间的顺序。可以推出的是，按块的平均权值大小来即可。用个堆维护一下即可。
虽然说着很简单，但是还是没有做出来。😤
[Ynoi Easy Round 2020] TEST_100
Solution
md，不知道为什么会做不出来这种sb构式题😇 我们考虑到可以分块对于每个块去维护它变化的函数。如果直接暴力维护转折点的话会有 \(2^s\) 个，其中 \(s\) 为块长，那么就会直接爆炸😶不过配合上值域 \(\le 10^5\) 的话可以做到 \(\mathcal O {(n^2/\log n)}\)，但是这个题过不了。
假设预处理当前块 \(x\to f(x)\)，那么我们可以把 \(f(x)\) 相同的 \(x\) 塞进一个并查集里面，后面显然它们会一起考虑。然后发现每个时刻的值域段都是连续的。假设我们需要加入 \(v\)，那么如果 \(v\) 在段外，那么相当于位移或者翻转再位移，如果 \(v\) 在段中，那么相当于把短的往长的折叠，可以发现一个点只会被折叠一次，所以直接暴力维护一下就对了。复杂度 \(\mathcal O(n\sqrt n)\)。
[Ynoi2018] 天降之物
Solution
哈哈哈哈哈哈哈哈，被狗是题目填满了😋😋😋 根号分治，主要问题在于小的加入到大的里面，发现直接暴力加复杂度就是对的，因为小的大小总数 \(\le n\)，大的个数 \(\sqrt n\)，所以最多 \(\mathcal O(n\sqrt n)\)。
[AGC043D] Merge Triplets
Solution
笔记本拿去修了，emoji不太好打😅 被橄榄了，果然比起AGC还是睡觉更适合我😪😪😪
我们可以看出对于当前这个序列，找到最大值位置，如果到末端的位置个数 \(>3\) 则显然不合法，否则我们删掉从最大值到末端，继续递归下去。然后考虑把每次删除的块提出来，然后发现可以长度为 \(1,2\) 的相互匹配，\(1\) 自己匹配，如果最后的块数 \(\le n\)，那么即是合法的。然后通过代数推导可以得到长度为 \(1\) 的个数 $\ge $ 长度为 \(2\) 的个数时即合法。（这一步如果这样推大概率时想不到的）另外一种自然的想法是，一开始都是长度为 \(3\) 的块，每次进行拆分，要么把长度为 \(3\) 的拆成长度为 \(1,2\) 的块，或者长度为 \(2\) 的再拆成两个长度为 \(1\) 的。可以发现 \(1\) 的个数 \(\ge\) \(2\) 的个数时即合法。
[AGC060C] Large Heap
Solution
又被橄榄了，哈哈哈哈哈哈哈😅😅😅😊😊😊
我们考虑算方案，可以发现我们可以考虑把 \(1\to u\) 以及 \(1\to v\) 的链抽出来，然后给它们赋上相对权值。那么只需要两条链分别递增即可，那么即是每次移动一端。我们考虑从下至上倒着推，这样初始值会好赋一点。一个小问题是每次还需要加入一整个子树，感性理解一下的话应该是跟子树大小正相关的，然后就可以直接算概率而不用算方案了。证明的话可以直接列式子算，这里就不赘述了。复杂度 \(\mathcal O(n^2)/\mathcal O(n^2\log )\)。
[AGC058D] Yet Another ABC String
Solution
AGC真是太棒了哈哈哈哈哈哈哈，我还是直接睡觉得了😴😴😴
我们考虑容斥，发现似乎不好弄，因为端可能相交，计算的话就会爆炸。不过可以发现的是，相交的段一定会构成连续一段，其中是类似 \(\text{ABCABC...}\) 的循环，每个长度为 \(3\) 的段都会产生贡献。那么我们可以只考虑钦定段尾，则段尾后面不能是开头的字符。然后直接算一下就好了，即把剩下的放进 \(i+1\) 个空隙里面。一个简单的计算方法是先放剩下的，划分成 \(i+1\) 段，再把这 \(i\) 个放进去，因为这样就可以确定每个的放置方法。复杂度 \(\mathcal O(n)\)。
[AGC001F] Wide Swap
Solution
有很多种做法，我这里都写一下吧（毕竟一个都没有想出来🙄🙄🙄
第一种做法即是我们考虑设 \(q\) 为 \(P\) 的逆排列，那么可以看出，题目被转化成了当 \(|q_i-q_{i+1}|\ge K\) 时，可以交换 \(q_i,q_{i+1}\)。可以发现的是，当存在 \(i,j\) 使得 \(|q_i-q_j|\le K\) 的时候那么 \(i,j\) 的相对大小关系是不会改变的。可以发现这时候我们就相当于建出了一个 DAG，需要使得topo序的逆排列最小。这跟 [HNOI2015]菜肴制作 差不多了，可以建反图然后按编号从大到小来 topo。这个题里面用线段树优化一下即可。
另外一种做法是考虑归并。我们还是需要先找到逆排列 \(q\)。考虑到右边的元素 \(i\) 如果能换到左边的 \(j\) 之前并且交换之后更优，那么一定有 \(q_i+K\le \min_{k=j}^{\text{mid}} q_k\)。那么直接归并一下就好了。
复杂度都为 \(\mathcal O(n\log n)\)，我实现的第二种。感觉这个题是可做的，不知道为什么没有什么思路，估计是看到AGC和排列就已经本能害怕了😟😟😟
[AGC002F] Leftmost Ball
Solution
没想到会被这种题目打败😇🥵 我们发现只需要满足任意前缀白球个数 \(\ge\) 不同颜色种数，那么即是合法的。那我们就可以设 \(f_{i,j}\) 表示现在放了 \(i\) 个白球，\(j\) 种颜色的方案数，每次要么把白球放在第一个空位，要么把一种新颜色放在第一个空位，并把剩下的 \(K-2\) 个放入别的空位里面。复杂度 \(\mathcal O(n^2)\)。
我被卡住的原因大抵是因为我没有往前缀方面考虑，而在想第一个出现的颜色🙃🙃🙃
[AGC004F] Namori
Solution
这种级别的题目就好像可以做，好像又不可以做，难受死了😇🤡
我们考虑先二分图染色（先不考虑奇环的情况），那么题目就变成了每次可以交换相邻的黑点和白点，问每个点都变成相反的情况。如果在树的情况下面，那么很显然我们可以对于一个点考虑其子树内移出子树外的贡献。假设黑点权值为 \(1\)，白点权值为 \(-1\)，子树权值为 \(w_x\)，那么答案显然即是 \(\sum |w_x|\) 。
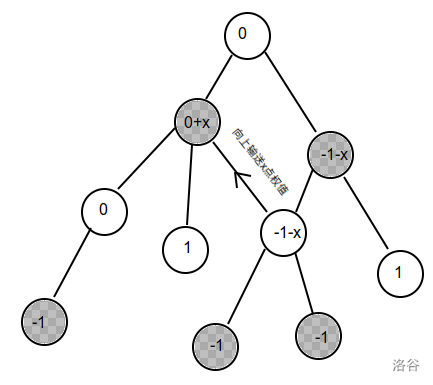
考虑偶环的情况。可以发现相当于我们在环边（指的是返祖边）可以选择从下面的点往上面传 \(x\) 个黑点/白点，大概如图（借一下题解老哥的图）：
那么在实际的 dfs 树中，因为返祖边一定连链头和链尾，那么就是选择一个 \(x\) 使得 \(\sum |w_u-x|+|-x|\)，其中 \(u\) 不考虑链头。那么可以看出 \(x\) 取中位数即最优。
再考虑奇环的情况。可以看出会存在相邻两个染色相同的情况。放在原问题上面考虑（下面所指颜色与二分图染色无关），当两个都是黑色时，可以变为白色，两个都是白色时可以变为黑色。那我们就可以利用它们去修改初始二分图染色情况。具体来说，我们可以把两个相同颜色的节点换到这里，然后它们就变了色。所以这条边被操作的次数就是固定了的，即二分图染色颜色差 \(/2\) 。然后剩下的部分按树的方法来即可。可以看出这个下界是可以达到的。
GYM104090E Oscar is All You Need
Solution
这个老哥讲的挺好的，这里就不赘述了。😋
