题解 [NOIP2020] 移球游戏

link

Solution

又回想起一年前被这个题目支配的恐惧，NOIP 就因为这个 sb 东西被拉开分差导致后面一个学期状态都很崩溃。唉，还是自己太菜了。。。

首先我们可以先考虑 \(n=2\) 的情况，你发现这个时候存在一种优秀方案使得可以 \(\Theta(m)\) 完成。如下图（图是嫖的，不想自己画了）

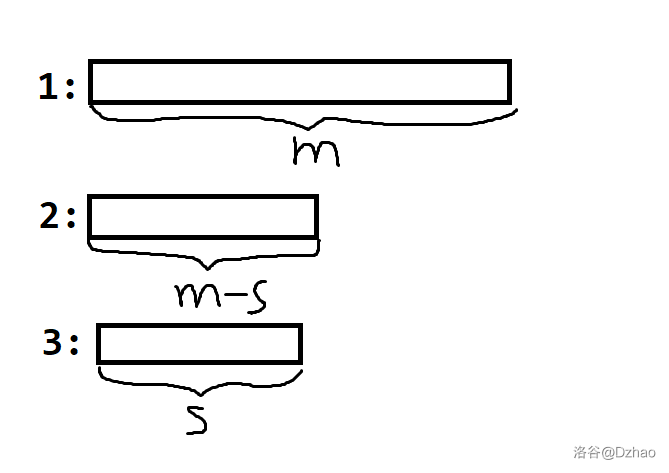
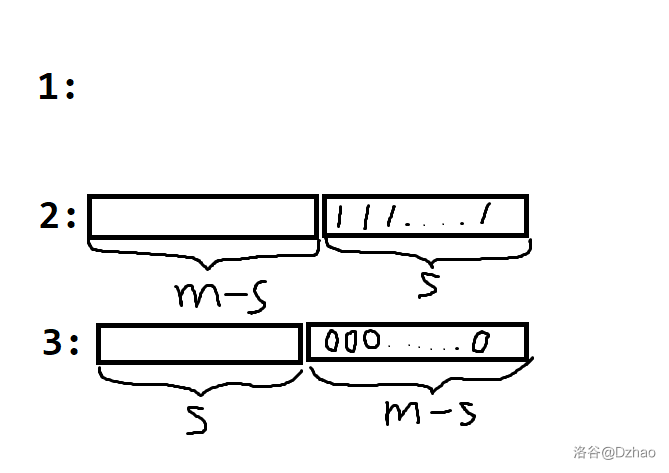
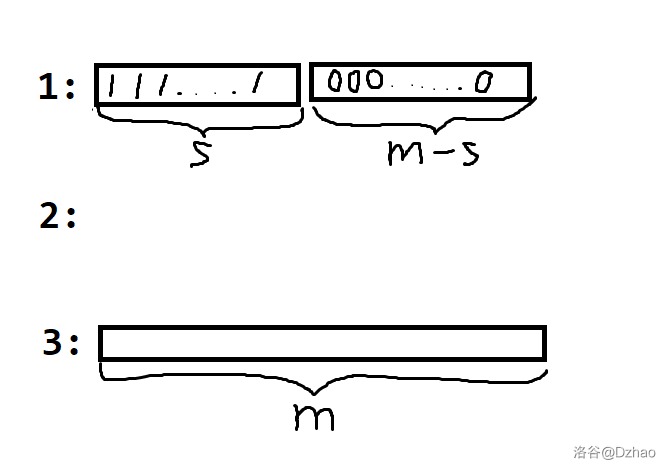
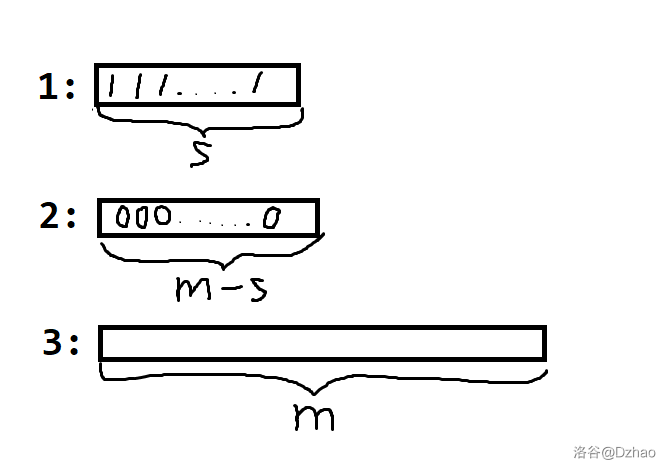
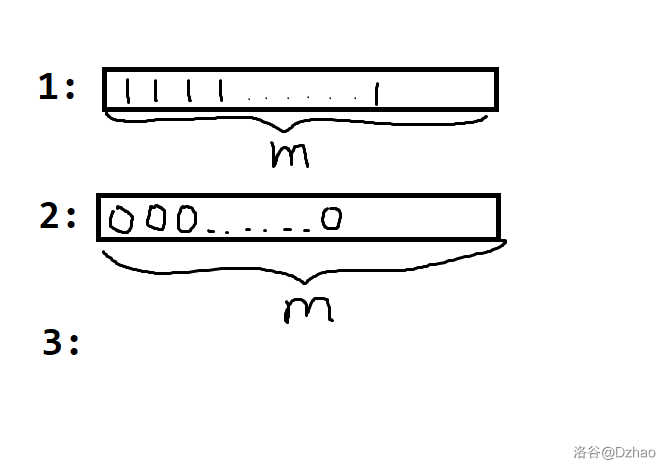
考虑 \(n>2\) 的情况。考虑分治，现在对 \([l,r]\) 进行处理。那么，如果我们可以将 \([l,mid]\) 颜色的球都放在 \([l,mid]\) 内，\([mid+1,r]\) 颜色的球都放在 \([mid+1,r]\) 内那么现在就可以做了。

然后你发现可以 \([l,mid]\) 和 \([mid+1,r]\) 之间的柱子两两操作满足这个，即每次把颜色多的那一边复原。

操作次数似乎是 \(\Theta(5nm\log n)\) 的。

Code

#include <bits/stdc++.h>
using namespace std;
 
#define Int register int
#define MAXM 405
#define MAXN 55

template <typename T> inline void read (T &t){t = 0;char c = getchar();int f = 1;while (c < '0' || c > '9'){if (c == '-') f = -f;c = getchar();}while (c >= '0' && c <= '9'){t = (t << 3) + (t << 1) + c - '0';c = getchar();} t *= f;}
template <typename T,typename ... Args> inline void read (T &t,Args&... args){read (t);read (args...);}
template <typename T> inline void write (T x){if (x < 0){x = -x;putchar ('-');}if (x > 9) write (x / 10);putchar (x % 10 + '0');}
template <typename T> inline void chkmax (T &a,T b){a = max (a,b);}
template <typename T> inline void chkmin (T &a,T b){a = min (a,b);}

bool flg[MAXN];
int n,m,cnt,top[MAXN],a[MAXN][MAXM],ans[820005][2];

void move (int x,int y){
	ans[++ cnt][0] = x,ans[cnt][1] = y;
	a[y][++ top[y]] = a[x][top[x] --];
}

void solve (int l,int r){
	if (l == r) return ;
	int mid = l + r >> 1;
	memset (flg,0,sizeof (flg));
	for (Int i = l;i <= mid;++ i)
		for (Int j = mid + 1;j <= r;++ j){
			if (flg[i] || flg[j]) continue;
			int s = 0;
			for (Int k = 1;k <= m;++ k) s += (a[i][k] <= mid) + (a[j][k] <= mid);
			if (s >= m){//还原第i根柱子 
				s = 0;
				for (Int k = 1;k <= m;++ k) s += (a[i][k] <= mid);
				for (Int k = 1;k <= s;++ k) move (j,n + 1);
				while (top[i]) if (a[i][top[i]] <= mid) move (i,j);else move (i,n + 1);
				for (Int k = 1;k <= s;++ k) move (j,i); 
				for (Int k = 1;k <= m - s;++ k) move (n + 1,i);
				for (Int k = 1;k <= m - s;++ k) move (j,n + 1);
				for (Int k = 1;k <= m - s;++ k) move (i,j);
				while (top[n + 1]) if (top[i] < m && a[n + 1][top[n + 1]] <= mid) move (n + 1,i);else move (n + 1,j);
				flg[i] = 1;
			}
			else{
				s = 0,swap (i,j);
				for (Int k = 1;k <= m;++ k) s += (a[i][k] > mid);
				for (Int k = 1;k <= s;++ k) move (j,n + 1);
				while (top[i]) if (a[i][top[i]] > mid) move (i,j);else move (i,n + 1);
				for (Int k = 1;k <= s;++ k) move (j,i); 
				for (Int k = 1;k <= m - s;++ k) move (n + 1,i);
				for (Int k = 1;k <= m - s;++ k) move (j,n + 1);
				for (Int k = 1;k <= m - s;++ k) move (i,j);
				while (top[n + 1]) if (top[i] < m && a[n + 1][top[n + 1]] > mid) move (n + 1,i);else move (n + 1,j);
				swap (i,j),flg[j] = 1;
			}
		}
	solve (l,mid),solve (mid + 1,r);
}

signed main(){
	read (n,m);
	for (Int i = 1;i <= n;++ i){
		top[i] = m;
		for (Int j = 1;j <= m;++ j) read (a[i][j]);
	}
	solve (1,n),write (cnt),putchar ('\n');
	for (Int i = 1;i <= cnt;++ i) write (ans[i][0]),putchar (' '),write (ans[i][1]),putchar ('\n');
	return 0;
}