题解 最小生成树

题目传送门

题目大意

给出一个 \(n\) 个点 \(m\) 条边的图，每次可以将一条边权值 +1，问最少操作多少次使得给定边一定出现在最小生成树里。

\(n\le 500,m\le 800\)

思路

tmd，一开始一直在想怎么找环之后直接搞，后来发现不是很好弄，然后数据范围也很迷惑，然后我猜这是个网络流，但是死活想不出来怎么建图，看了题解之后就悟了。。。（

不难发现假如我们需要 \((u,v,w)\) 一定出现，可以发现存在一条 \(u\to v\) 的路径使得该路径权值最大值不超过 \(w\) 是这条边不一定出现的充必条件。可以考虑 kruskal 的过程即可证明。

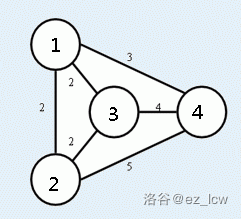
以样例为例，可以发现 \(1\to 2\) 存在 \(1\to 2\to 3\) 满足条件。

于是，我们要做的就是对于每一条满足条件的路径把最大值加到 \(w+1\)，但是每一条边只加一次。于是我们就可以想到最小割。

时间复杂度 \(\Theta(n^2m)\)

\(\texttt{Code}\)

#include <bits/stdc++.h>
using namespace std;

#define Int register int
#define INF 0x7f7f7f7f
#define MAXM 805
#define MAXN 505

template <typename T> inline void read (T &t){t = 0;char c = getchar();int f = 1;while (c < '0' || c > '9'){if (c == '-') f = -f;c = getchar();}while (c >= '0' && c <= '9'){t = (t << 3) + (t << 1) + c - '0';c = getchar();} t *= f;}
template <typename T,typename ... Args> inline void read (T &t,Args&... args){read (t);read (args...);}
template <typename T> inline void write (T x){if (x < 0){x = -x;putchar ('-');}if (x > 9) write (x / 10);putchar (x % 10 + '0');}

int n,m,S,T,lab,toop = 1,cur[MAXN],dep[MAXN],head[MAXN];
struct edge{
	int v,w,nxt;
}e[MAXM * MAXM];

struct Edge{
	int u,v,w;
}bri[MAXM];

void Add_Edge (int u,int v,int w){
	e[++ toop] = edge {v,w,head[u]},head[u] = toop;
	e[++ toop] = edge {u,w,head[v]},head[v] = toop;
}

bool BFS (){
	queue <int> q;memset (dep,-1,sizeof (dep)),dep[S] = 0,q.push (S);
	while (!q.empty()){
		int u = q.front();q.pop ();
		for (Int i = head[u];i;i = e[i].nxt){
			int v = e[i].v,w = e[i].w;
			if (w && dep[v] == -1) dep[v] = dep[u] + 1,q.push (v);
		}
	}
	return dep[T] != -1;
}

int dfs (int u,int flow){
	if (u == T) return flow;
	int res = 0;
	for (Int &i = cur[u];i && flow;i = e[i].nxt){
		int v = e[i].v,w = e[i].w,cur;
		if (w && dep[v] == dep[u] + 1) cur = dfs (v,min (flow,w)),res += cur,flow -= cur,e[i].w -= cur,e[i ^ 1].w += cur;
	}
	if (!flow) dep[u] = -1;
	return res;
}

int Maxflow (){
	int ans = 0;
	while (BFS ()){
		memcpy (cur,head,sizeof (head));
		ans += dfs (S,INF);
	}
	return ans;
} 

signed main(){
	read (n,m,lab);
	for (Int i = 1;i <= m;++ i) read (bri[i].u,bri[i].v,bri[i].w);S = bri[lab].u,T = bri[lab].v;
	for (Int i = 1;i <= m;++ i) if (i != lab && bri[i].w <= bri[lab].w) Add_Edge (bri[i].u,bri[i].v,bri[lab].w - bri[i].w + 1);
	write (Maxflow ()),putchar ('\n');
	return 0;
}